Metoda celor doua faze

METODA CELOR DOUA FAZE

Pentru aplicarea algorimului simplex este necesara existenta unei baze initiale, de dorit matrice unitate, deci a unui program de baza initial. Mentionam doua metode pentru determinarea unui program de baza initial: metoda celor doua faze si metoda penalitatii. Vom prezenta in continuare prima dintre metodele mentionate.

Prima faza ne permite sa determinam o baza initiala  (in cazul in care aceasta exista).

Ne propunem sa rezolvam problema:

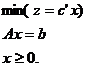(11)

Etapa 1. Se rezolva problema de programare liniara:

       (12)

Am presupus , , fiind vectorul variabilelor artificiale.

Observatii. (i). Nu este necesar sa se introduca m variabile artificiale. Este insa necesar sa se introduca atatea variabile artificiale cati vectori unitari lipsesc pentru a forma o baza unitara.

(ii). Problema (12) se poate scrie in detaliu astfel:

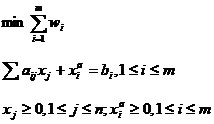(12

(iii). Problema (12) poseda un program de baza initial (in limbaj geometric, multimea P_a a programelor problemei (12) poseda un varf) de forma:

.

(iv). Valoarea minima a functiei obiectiv a problemei (12) este .

(v). Daca  atunci multimea P a programelor problemei (11) este vida.

(vi). Daca  atunci, indiferent de faptul ca nici-o variabila artificiala nu este variabila de baza, sau ca exista cel putin o variabila artificiala de baza (evident cu valoare nula), un varf al multimii P_a programelor problemei (12) este un varf al multimii P a programelor problemei (11), caz in care se trece la etapa 2.

Etapa 2. Se rezolva problema initiala, pornind cu baza obtinuta in finalul etapei 1. Daca atunci etapa a doua este consistenta, in caz contrar etapa a doua este inconsistenta, problema initiala neadmitand programe de baza.

Observatii. (i). Daca nici-o variabila artificiala nu face parte din baza, se aplica algoritmul simplex pentru multimea P si functia obiectiv z pana se obtine optimul.

(ii). Daca exista cel putin o variabila artificiala in baza, aplicam algoritmul simplex pentru multimea P_a, cu mentiunea ca ne restrangem numai la muchiile lui P_a, care mentin valoarea nula a lui w, caz in care programul optim (varful optim) va apartine si lui P.

Observatie. Din relatiile (5), (7) si (8) rezulta ca in cadrul unei iteratii simplex, pentru calculul elementelor tabelului simplex este suficienta cunoasterea inversei bazei curente, adica B^-1.

Deoarece nu toate elementele tabelului simplex sunt necesare in cadrul unei iteratii, iar calculul tuturor elementelelor scade eficienta algoritmului, prezentam in continuare algoritmul simplex-revizuit care constituie o varianta "mai economica" a algoritmului simplex. Aceasta varianta este recomandata indeosebi atunci cand n >> m

Tabelul algoritmului simplex-revizuit are urmatoarea forma:

Prima linie a tabelului corespunde primei faze (daca aceasta este necesara), iar cea de a doua linie a tabelului corespunde celei de a doua faze.

In cadrul algoritmului simplex-revizuit un rol deosebit il joaca matricea incadrata din tabelul asociat acestuia si matricea extinsa, adica matricea:

.

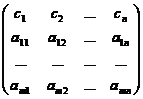Observatii: (i).  ;

(ii).

(iii). ;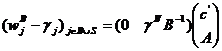

(iv). ;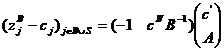

(v).