
|
|
|
APLICATIE - regresie liniara simpla
Pentru 15 agenti de asigurari, angajati ai unei companii de asigurari de viata, se cunosc datele privind timpul mediu (in minute) petrecut de un agent cu un potential client si numarul de polite incheiate de fiecare intr-o saptamana.
|
Timpul mediu (min.) |
25 |
23 |
30 |
25 |
20 |
33 |
18 |
21 |
22 |
30 |
26 |
26 |
27 |
29 |
20 |
|
Nr. polite |
10 |
11 |
14 |
12 |
8 |
18 |
9 |
10 |
10 |
15 |
11 |
15 |
12 |
14 |
11 |
Se cere:
a) Construiti si comentati graficul realizat pe baza datelor privind timpul mediu (in minute) petrecut de un agent cu un potential client si numarul de polite incheiate intr-o saptamana, pentru toti cei 15 angajati.
b) Sa se estimeze parametrii modelului liniar de regresie si sa se testeze semnificatia parametrilor modelului pentru un prag de semnificatie a = 0,05;
c) Testati validitatea modelului de regresie pentru un nivel de semnificatie a = 0,05;
d) Sa se determine erorile reziduale;
e) Masurati intensitatea legaturii dintre cele doua variabile folosind atat coeficientul cat si raportul de corelatie, testand semnificatia celor doi indicatori utilizati, pentru un nivel de incredere de 95%;
f) Efectuati o previzionare punctuala si pe interval de incredere a numarului de polite incheiate de un agent care petrece in medie 24 de minute cu un potential client.
Rezolvare
OBSERVATIE!
Se identifica cele doua variabile:
xi - variabila factoriala = timpul mediu (in minute) petrecut de un agent cu un potential client
yi - variabila dependenta = numarul de polite incheiate intr-o saptamana de fiecare agent
a) Construirea si comentarea graficului
Graficul construit, denumit corelograma, ne indica existenta, forma si directia legaturii dintre cele doua variabile:
Corelograma dintre timpul mediu petrecut de un agent cu un potential client
si numarul de polite incheiate de fiecare agent intr-o saptamana
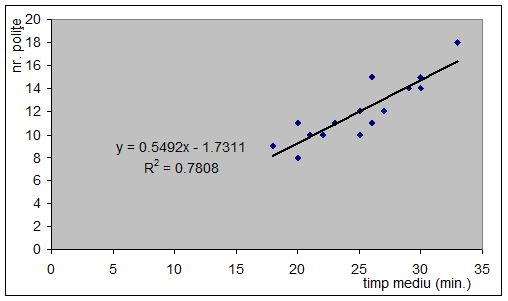
Corelograma evidentiaza legatura directa (punctele sunt plasate pe directia primei bisectoare) si liniara (dreapta de regresie are panta pozitiva) dintre timpul mediu petrecut de un agent cu un potential client si numarul de polite incheiate de fiecare agent
b) b.1. Estimarea parametrilor modelului liniar de regresie (a, b)
Aplicarea modelului
liniar de regresie presupune utilizarea ecuatiei de regresie liniara:![]()
Parametrii a si b se determina cu ajutorul metodei celor mai mici patrate:
![]() aplicarea ei conducand
la obtinerea sistemului de ecuatii normale:
aplicarea ei conducand
la obtinerea sistemului de ecuatii normale: , unde
, unde ![]() angajati
angajati
Pentru a rezolva sistemul vom folosi urmatorul tabel in care sunt prezentate valorile intermediare:
|
Timpul
mediu (min.) |
Nr. Polite |
|
|
|
|
25 |
10 |
625 |
250 |
12 |
|
23 |
11 |
529 |
253 |
10,9016 |
|
30 |
14 |
900 |
420 |
14,7462 |
|
25 |
12 |
625 |
300 |
12 |
|
20 |
8 |
400 |
160 |
9,254 |
|
33 |
18 |
1089 |
594 |
16,3936 |
|
18 |
9 |
324 |
162 |
8,1556 |
|
21 |
10 |
441 |
210 |
9,8032 |
|
22 |
10 |
484 |
220 |
10,3524 |
|
30 |
15 |
900 |
450 |
14,7462 |
|
26 |
11 |
676 |
286 |
12,5492 |
|
26 |
15 |
676 |
390 |
12,5492 |
|
27 |
12 |
729 |
324 |
13,0984 |
|
29 |
14 |
841 |
406 |
14,1968 |
|
20 |
11 |
400 |
220 |
9,254 |
|
|
|
|
|
|
Sistemul de
ecuatii normale devine:![]() ,unde
,unde
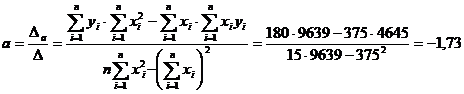
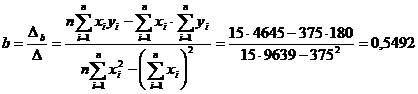
Deci:![]()
Interpretare: b = + 0,5492
se numeste coeficient de regresie reprezentand panta liniei drepte
b> 0, deci intre timpul mediu petrecut de un agent cu un potential client si numarul de polite incheiate de fiecare agent exista o legatura directa
la cresterea cu un minut a timpul mediu petrecut de un agent cu un potential client, numarul de polite incheiate se mareste cu 0,5495 (deci intr-un minut se completeaza o jumatate de polita)
b.2. Testarea semnificatiei parametrilor modelului
Ecuatia de
regresie - la nivelul colectivitatii generale este: ![]()
- la nivelul esantionului este: ![]()
Testarea semnificatiei parametrului a
H0 a = 0(adica a nu este semnificativ diferit de zero, deci a nu este semnificativ statistic)
H1 a 0, (adica a este semnificativ diferit de zero, deci a este semnificativ statistic)
Deoarece n = 15 < 30 avem esantion de volum redus si pentru testare vom utiliza testul t.
Stiind
ca pragul de semnificatie este ![]() si
si ![]() (exista un singur factor de influenta) se
stabileste:
(exista un singur factor de influenta) se
stabileste:
valoarea
critica: ![]()
regiunea
de respingere: daca ![]() , sau
, sau ![]() atunci H0 se respinge
atunci H0 se respinge
Determinarea statisticii
testului ( tcalculat ) are la baza relatia : 
|
|
|
|
|
|
|
|
25 |
10 |
12 |
4 |
625 |
0 |
|
23 |
11 |
10,9016 |
0,0097 |
529 |
4 |
|
30 |
14 |
14,7462 |
0,5568 |
900 |
25 |
|
25 |
12 |
12 |
0 |
625 |
0 |
|
20 |
8 |
9,254 |
1,5725 |
400 |
25 |
|
33 |
18 |
16,3936 |
2,5805 |
1089 |
64 |
|
18 |
9 |
8,1556 |
0,7130 |
324 |
49 |
|
21 |
10 |
9,8032 |
0,0387 |
441 |
16 |
|
22 |
10 |
10,3524 |
4,151 |
484 |
9 |
|
30 |
15 |
14,7462 |
0,0644 |
900 |
25 |
|
26 |
11 |
12,5492 |
2,4000 |
676 |
1 |
|
26 |
15 |
12,5492 |
6,0064 |
676 |
1 |
|
27 |
12 |
13,0984 |
1,2065 |
729 |
4 |
|
29 |
14 |
14,1968 |
0,0387 |
841 |
16 |
|
20 |
11 |
9,254 |
3,0485 |
400 |
25 |
|
|
|
|
|
|
|
a = - 1,73
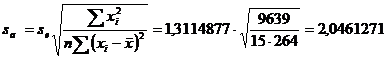
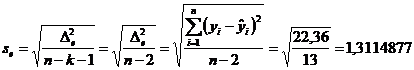
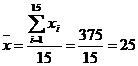
Statistica
testului:![]()
Concluzia:
deoarece ![]() (
(![]() ) , deci H0
se accepta , ceea
ce insemna ca a nu este
semnificativ diferit de zero (a nu este
semnificativ statistic)
) , deci H0
se accepta , ceea
ce insemna ca a nu este
semnificativ diferit de zero (a nu este
semnificativ statistic)
Intervalul de incredere este: ![]()
![]()
![]()
Testarea
semnificatiei parametrului ![]()
H0 :![]() = 0(panta
= 0(panta ![]() este zero, adica
este zero, adica ![]() nu este semnificativ
diferit de zero, deci
nu este semnificativ
diferit de zero, deci ![]() nu este semnificativ
statistic)
nu este semnificativ
statistic)
H1 ![]() 0, (panta
0, (panta
![]() nu este diferita de
zero, adica
nu este diferita de
zero, adica ![]() este semnificativ diferit
de zero, deci
este semnificativ diferit
de zero, deci ![]() este semnificativ
statistic)
este semnificativ
statistic)
Deoarece n = 15 < 30 avem esantion de volum redus si pentru testare vom utiliza testul t.
Stiind
ca pragul de semnificatie este ![]() si
si ![]() (exista un singur factor de influenta) se
stabileste:
(exista un singur factor de influenta) se
stabileste:
valoarea
critica: ![]()
regiunea
de respingere: daca ![]() sau
sau ![]() atunci H0 se respinge
atunci H0 se respinge
Determinarea
statisticii testului ( tcalculat ) are la baza relatia: ![]()
|
|
|
|
|
|
|
25 |
10 |
12 |
4 |
0 |
|
23 |
11 |
10,9016 |
0,0097 |
4 |
|
30 |
14 |
14,7462 |
0,5568 |
25 |
|
25 |
12 |
12 |
0 |
0 |
|
20 |
8 |
9,254 |
1,5725 |
25 |
|
33 |
18 |
16,3936 |
2,5805 |
64 |
|
18 |
9 |
8,1556 |
0,7130 |
49 |
|
21 |
10 |
9,8032 |
0,0387 |
16 |
|
22 |
10 |
10,3524 |
4,151 |
9 |
|
30 |
15 |
14,7462 |
0,0644 |
25 |
|
26 |
11 |
12,5492 |
2,4000 |
1 |
|
26 |
15 |
12,5492 |
6,0064 |
1 |
|
27 |
12 |
13,0984 |
1,2065 |
4 |
|
29 |
14 |
14,1968 |
0,0387 |
16 |
|
20 |
11 |
9,254 |
3,0485 |
25 |
|
|
|
|
|
|
b = 0,5492
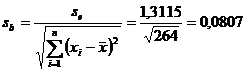
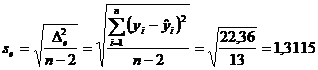
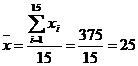
Statistica
testului este:![]()
Concluzia:
deoarece ![]() (
(![]() ) , deci H0 se respinge , ceea
ce insemna ca H1 se accepta, deci
) , deci H0 se respinge , ceea
ce insemna ca H1 se accepta, deci ![]() este semnificativ diferit
de zero (
este semnificativ diferit
de zero (![]() este semnificativ statistic)
este semnificativ statistic)
Intervalul de incredere este: ![]()
![]()
![]()
Rezolvarea punctului b al aplicatiei cu ajutorul programului informatic EXCEL
Se selecteaza din meniul principal optiunea Tools -- Data Analysis; la selectarea optiunii Regression apare o fereastra in care se va completa astfel:
la Input Y Range: $B$1:$B$16
la Input X Range: $A$1:$A$16
se bifeaza Labels
se activeaza Output Range si se selecteaza o celula (exemplu: $D$1), unde vor apare mai multe tabele cu rezultatele, printre care se regaseste si tabelul urmator:
|
|
|
Coefficients
|
Standard Error
|
t Stat
|
P-value
|
Lower 95%
|
Upper 95%
|
Intercept
|
-1.731061
|
2.046120
|
-0.846021
|
0.412843
|
-6.151434
|
2.689313
|
Timpul mediu
|
0.549242
|
0.080716
|
6.804611
|
0.000013
|
0.374866
|
0.723619 |
Tabel 3
Coefficients
Standard Error
t Stat
P-value
Lower 95%
Upper 95%
Coeficientii
(parametrii)
ecuatiei de regresie liniara
Abaterea medie patratica
Statistica testului
tcalc
Pragul critic
trebuie comparat cu cel de semnificatie
Limita inferioara
a intervalului
de incredere
Limita superioara
a intervalului
de incredere
Intercept
(termenul liber)
a -1,731061
![]() 2,046120
2,046120
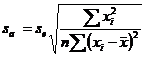
![]() -0,846021
-0,846021
![]()
![]() = 0,412843
= 0,412843
-6.151434
![]()
2.689313
![]()
Timpul mediu
(factorul de influenta)
b 0,549242
![]() 0,080716
0,080716
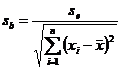
![]() 6,804611
6,804611
![]()
![]() =
=
0,000013
0.374866
![]()
0.723619
![]()
Observatie: valoarea
abaterii medii patratice a
erorilor in esantion (![]() ) este preluata din tabelul 1 Excel -- SUMMARY OUTPUT (Standard Error
) este preluata din tabelul 1 Excel -- SUMMARY OUTPUT (Standard Error ![]() )
)
Interpretarea rezultatelor din tabelul 3
Coeficientii (parametrii) ecuatiei de regresie liniara (![]() si
si ![]() ) ne conduc la scrierea urmatoarei functii de
regresie liniare:
) ne conduc la scrierea urmatoarei functii de
regresie liniare: ![]() , in care:
, in care:
Se observa ca parametrul ![]() nu este semnificativ
statistic deoarece:
nu este semnificativ
statistic deoarece:
pragul critic P-value![]() 0,412843 > pragul
de semnificatie
0,412843 > pragul
de semnificatie ![]()
limita inferioara a
intervalului de incredere (lower 95% = - 6,15) este cu semn contrar fata
de limita superioara a intervalului (upper 95% = + 2,689); intervalul de
incredere este ![]() ;
;
iar, rezultatul statisticii testului (![]() - 0,846021) este mai mica fata
de valoarea critica tabelara
- 0,846021) este mai mica fata
de valoarea critica tabelara![]()
Se observa ca parametrul ![]() este semnificativ
statistic deoarece:
este semnificativ
statistic deoarece:
pragul critic P-value![]() 0,000013 < pragul de semnificatie
0,000013 < pragul de semnificatie ![]() ;
;
limita inferioara a
intervalului de incredere (lower 95% = + 0,374866) are acelasi semn cu
limita superioara a respectivului interval (upper 95% = + 0,723619 intervalul de incredere este ![]()
iar, rezultatul statisticii testului (![]() 6,804611) este mai mare
fata de valoarea critica tabelara
6,804611) este mai mare
fata de valoarea critica tabelara![]()
c) Testarea validitatii modelului de regresie
H0: modelul nu este valid statistic
(imprastierea valorilor ![]() datorate factorului
timp nu difera semnificativ de imprastierea acelorasi
valori datorate intamplarii)
datorate factorului
timp nu difera semnificativ de imprastierea acelorasi
valori datorate intamplarii)
H1: modelul este valid statistict
Stiind
ca pragul de semnificatie este ![]() si
si ![]() (exista un singur factor de influenta) se
stabileste:
(exista un singur factor de influenta) se
stabileste:
valoarea
critica: ![]()
regiunea
de respingere: daca ![]() , atunci H0 se respinge
, atunci H0 se respinge
Determinarea
statisticii testului (![]() ) are la baza relatia:
) are la baza relatia: 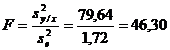
Pentru determinarea statisticii testului F se foloseste urmatorul algoritm de calcul:
|
Timpul
mediu (min.) |
Nr. Polite |
|
|
|
|
|
25 |
10 |
12 |
0 |
4 |
4 |
|
23 |
11 |
10,9016 |
1,2065 |
0,0097 |
1 |
|
30 |
14 |
14,7462 |
7,5416 |
0,5568 |
4 |
|
25 |
12 |
12 |
0 |
0 |
0 |
|
20 |
8 |
9,254 |
7,5405 |
1,5725 |
16 |
|
33 |
18 |
16,3936 |
19,3037 |
2,5805 |
36 |
|
18 |
9 |
8,1556 |
14,7794 |
0,7130 |
9 |
|
21 |
10 |
9,8032 |
4,8259 |
0,0387 |
4 |
|
22 |
10 |
10,3524 |
2,7146 |
4,151 |
4 |
|
30 |
15 |
14,7462 |
7,5416 |
0,0644 |
9 |
|
26 |
11 |
12,5492 |
0,3016 |
2,4000 |
1 |
|
26 |
15 |
12,5492 |
0,3016 |
6,0064 |
9 |
|
27 |
12 |
13,0984 |
1,2065 |
1,2065 |
0 |
|
29 |
14 |
14,1968 |
4,8259 |
0,0387 |
4 |
|
20 |
11 |
9,254 |
7,5405 |
3,0485 |
1 |
|
|
|
|
79,64 |
|
|
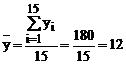 polite
polite
SS Sum of Squares --- suma patratelor varianta
SST=SSR + SSE
SSR=![]()
SS=![]()
SST=![]()
df --- degree of freedom --- grade de libertate
k 1
n - k - 1 = 13
n - 1 = k + (n - k - 1) = 1 + 13 = 14
MS --- media patratelor = dispersia corectata
MS = SS : df
![]()
![]()
![]() nu se determina
nu se determina
F testul F
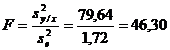
Concluzie:
Deoarece ![]() (46,30) >
(46,30) > ![]() (4,67) T
(4,67) T ![]() se respinge, deci
se respinge, deci ![]() este adevarata, prin urmare, modelul este valid.
este adevarata, prin urmare, modelul este valid.
Rezolvarea punctului c al aplicatiei cu ajutorul programului informatic EXCEL
Se selecteaza din meniul principal optiunea Tools -- Data Analysis; la selectarea optiunii Regression apare o fereastra in care se va completa astfel:
la Input Y Range: $B$1:$B$16
la Input X Range: $A$1:$A$16
se bifeaza Labels
se activeaza Output Range si se selecteaza o celula (exemplu: $D$1), unde vor apare tabele cu rezultate, printre care se regaseste si tabelul urmator:
|
|
Tabelul 2 ANOVA
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Significance F
|
Regression
|
1.000000
|
79.640152
|
79.640152
|
46.302727
|
0.000013
|
|
Residual
|
13.000000
|
22.359848
|
1.719988
|
|
|
|
Total
|
14.000000
|
102.000000
|
|
|
|
| |
Pentru aplicarea testului F se completeaza tabelul:
Sursa variatiei
df
(degree of freedom)
(grade de libertate)
SS
(Sum of Squares)
(suma patratelor varianta)
MS
=SS : df
(media patratelor
dispersia corectata)
F
(Statistica testul F
sau ![]() )
)
Significance F
probabilitatea critica)
Regression (variatia
datorata regresiei)
k
1
SSR=![]() 79,64
79,64
![]() =
=
79,640152
Testul
F=![]() /
/![]()
F = 46,302727
0,000013< 0,05
(resping H0 - model valid)
Residual
(variatia reziduala)
n-k-1
13
SS=![]() 22,36
22,36
![]() =
=
1,719988
Total (variatia totala)
n-1
14
SST=![]() = 102
= 102
SST=SSR + SSE
![]()
Nota: k - reprezinta numarul variabilelor factoriale (in cazul modelului unifactorial k = 1).
Interpretare rezultate din tabelul 2 ANOVA
In acest tabel este calculata statistica testului F pentru validarea modelului de regresie.
Modelul
de regresie construit (![]() ) este valid si poate fi utilizat pentru analiza
dependentei dintre cele doua variabile, intrucat:
) este valid si poate fi utilizat pentru analiza
dependentei dintre cele doua variabile, intrucat:
![]() (46,30) >
(46,30) > ![]() (4,67)
(4,67)
Significance
F (probabilitatea critica) este 0,000013 mai mica decat pragul de
semnificatie ![]() .
.
d) Stabilirea erorilor reziduale
Determinarea erorilor reziduale (ei) presupune calculul diferentelor dintre valorile empirice si cele teoretice (estimate) pentru fiecare agent de asigurari, astfel:
|
|
|
|
|
|
10 |
12 |
-2 |
|
|
11 |
10,9016 |
0,0984 |
|
|
14 |
14,7462 |
0,7462 |
|
|
12 |
12 |
0 |
|
|
8 |
9,254 |
1,254 |
|
|
18 |
16,3936 |
1,6064 |
|
|
9 |
8,1556 |
0,8444 |
|
|
10 |
9,8032 |
0,1968 |
|
|
10 |
10,3524 |
2,0374 |
|
|
15 |
14,7462 |
0,2538 |
|
|
11 |
12,5492 |
1,5492 |
|
|
15 |
12,5492 |
2,4508 |
|
|
12 |
13,0984 |
1,0984 |
|
|
14 |
14,1968 |
0,1968 |
|
|
11 |
9,254 |
1,746 |
Rezolvarea punctului d al aplicatiei cu ajutorul programului informatic EXCEL
Se selecteaza din meniul principal optiunea Tools -- Data Analysis; la selectarea optiunii Regression apare o fereastra in care se va completa astfel:
la Input Y Range: $B$1:$B$16
la Input X Range: $A$1:$A$16
se bifeaza Labels
se activeaza Output Range si se selecteaza o celula (exemplu: $D$1), unde vor apare tabele cu rezultate, printre care se regaseste si tabelul REZIDUAL OUTPUT:
|
|
RESIDUAL OUTPUT
|
|
|
|
|
|
|
Observation
|
Predicted Nr. Polite
|
Residuals
|
Standard Residuals
|
1
|
12
|
-2
|
-1.582557817
|
2
|
10.90151515
|
0.098484848
|
0.077928983
|
3
|
14.74621212
|
-0.746212121
|
-0.590461913
|
4
|
12
|
0
|
0
|
5
|
9.253787879
|
-1.253787879
|
-0.992095904
|
6
|
16.39393939
|
1.606060606
|
1.270841883
|
7
|
8.15530303
|
0.84469697
|
0.668390896
|
8
|
9.803030303
|
0.196969697
|
0.155857967
|
9
|
10.35227273
|
-0.352272727
|
-0.278745979
|
10
|
14.74621212
|
0.253787879
|
0.200816996
|
11
|
12.54924242
|
-1.549242424
|
-1.225882854
|
12
|
12.54924242
|
2.450757576
|
1.939232779
|
13
|
13.09848485
|
-1.098484848
|
-0.869207892
|
14
|
14.1969697
|
-0.196969697
|
-0.155857967
|
15
|
9.253787879
|
1.746212121
|
1.381740821 | |

Observatie: Pentru constructia graficului, se bifeaza Rezidual Plots.
Prezentarea detaliata a elementelor rezultate prin aplicarea programului EXCEL:
|
|
Observation (nr.agenti asigurari)
|
Predicted Nr. Polite (Nr. Politelor estimate pe baza functiei de regresie)
|
Residuals (valorile reziduale)
|
Standard Residuals
|
1
|
12
|
-2
|
-1.582557817
|
2
|
10.90151515
|
0.098484848
|
0.077928983
|
3
|
14.74621212
|
-0.746212121
|
-0.590461913
|
4
|
12
|
0
|
0
|
5
|
9.253787879
|
-1.253787879
|
-0.992095904
|
6
|
16.39393939
|
1.606060606
|
1.270841883
|
7
|
8.15530303
|
0.84469697
|
0.668390896
|
8
|
9.803030303
|
0.196969697
|
0.155857967
|
9
|
10.35227273
|
-0.352272727
|
-0.278745979
|
10
|
14.74621212
|
0.253787879
|
0.200816996
|
11
|
12.54924242
|
-1.549242424
|
-1.225882854
|
12
|
12.54924242
|
2.450757576
|
1.939232779
|
13
|
13.09848485
|
-1.098484848
|
-0.869207892
|
14
|
14.1969697
|
-0.196969697
|
-0.155857967
|
15
|
9.253787879
|
1.746212121
|
1.381740821 |
e) Masurarea intensitatii legaturii dintre timpul mediu petrecut de un agent cu un potential client si numarul de polite incheiate de fiecare agent
Intensitatea legaturii dintre cele doua variabile se poate stabili atat prin aplicarea coeficientului de corelatie liniara, dar si cu ajutorul raportului de corelatie (care se aplica atit pentru legaturile liniare, cat si in cazul legaturilor neliniare).
|
|
|
|
|
|
|
|
|
25 |
10 |
0 |
-2 |
0 |
0 |
4 |
|
23 |
11 |
-2 |
-1 |
2 |
4 |
1 |
|
30 |
14 |
5 |
2 |
10 |
25 |
4 |
|
25 |
12 |
0 |
0 |
0 |
0 |
0 |
|
20 |
8 |
-5 |
-4 |
20 |
25 |
16 |
|
33 |
18 |
8 |
6 |
48 |
64 |
36 |
|
18 |
9 |
-7 |
-3 |
21 |
49 |
9 |
|
21 |
10 |
-4 |
-2 |
8 |
16 |
4 |
|
22 |
10 |
-3 |
-2 |
6 |
9 |
4 |
|
30 |
15 |
5 |
3 |
15 |
25 |
9 |
|
26 |
11 |
1 |
-1 |
-1 |
1 |
1 |
|
26 |
15 |
1 |
3 |
3 |
1 |
9 |
|
27 |
12 |
2 |
0 |
0 |
4 |
0 |
|
29 |
14 |
4 |
2 |
8 |
16 |
4 |
|
20 |
11 |
-5 |
-1 |
5 |
25 |
1 |
|
|
|
|
|
|
|
|
Relatia de calcul este:
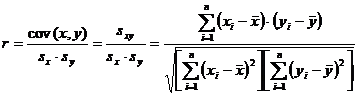 sau
sau 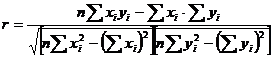

|
|
|
|
|
|
|
25 |
10 |
625 |
100 |
250 |
|
23 |
11 |
529 |
121 |
253 |
|
30 |
14 |
900 |
196 |
420 |
|
25 |
12 |
625 |
144 |
300 |
|
20 |
8 |
400 |
64 |
160 |
|
33 |
18 |
1089 |
324 |
594 |
|
18 |
9 |
324 |
81 |
162 |
|
21 |
10 |
441 |
100 |
210 |
|
22 |
10 |
484 |
225 |
220 |
|
30 |
15 |
900 |
121 |
450 |
|
26 |
11 |
676 |
225 |
286 |
|
26 |
15 |
676 |
144 |
390 |
|
27 |
12 |
729 |
196 |
324 |
|
29 |
14 |
841 |
121 |
406 |
|
20 |
11 |
400 |
|
220 |
|
|
|
|
|
|
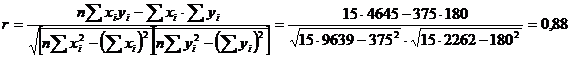
r = 0,88 > 0, ceea ce ne arata ca, intre timpul mediu petrecut de un agent cu un potential client si numarul de polite incheiate de fiecare agent exista o legatura directa puternica.
Testarea semnificatiei coeficientului de corelatie
- se
stabileste ipoteza nula ![]() (coeficientul de
corelatie al colectivitatii din care s-a extras esantionul
de 15 angajati, nu difera semnificativ de zero, deci nu este semnificativ statistic);
(coeficientul de
corelatie al colectivitatii din care s-a extras esantionul
de 15 angajati, nu difera semnificativ de zero, deci nu este semnificativ statistic);
- se
stabileste ipoteza alternativa ![]() (coeficientul de corelatie al colectivitatii
din care s-a extras esantionul de 15 angajati, difera
semnificativ de zero, deci este
semnificativ statistic);
(coeficientul de corelatie al colectivitatii
din care s-a extras esantionul de 15 angajati, difera
semnificativ de zero, deci este
semnificativ statistic);
Stiind
ca pragul de semnificatie este ![]() si
si ![]() (exista un singur factor de influenta) se
stabileste:
(exista un singur factor de influenta) se
stabileste:
valoarea
critica: ![]()
regiunea
de respingere: daca ![]() atunci H0 se
respinge
atunci H0 se
respinge
Determinarea statisticii testului ( tcalculat ) are la baza relatia:
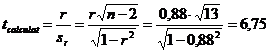
Concluzie:
Deoarece ![]() T
T ![]() se respinge, deci
se respinge, deci ![]() este adevarata, prin urmare coeficientul de
corelatie al colectivitatii din care s-a extras esantionul
de 15 angajati, difera semnificativ de zero, deci este semnificativ statistic.
este adevarata, prin urmare coeficientul de
corelatie al colectivitatii din care s-a extras esantionul
de 15 angajati, difera semnificativ de zero, deci este semnificativ statistic.
Raportul de corelatie -- se utilizeaza atat in cazul legaturilor liniare, cat si in situatia celor de tip neliniar
Masurarea intensitatii legaturii cu raportul de corelatie R presupune aplicarea relatiei:
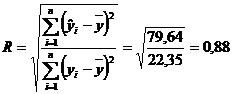
Rezultatul R = 0,88 ne arata ca, intre timpul mediu petrecut de un agent cu un potential client si numarul de polite incheiate de fiecare agent exista o legatura puternica.
Deoarece R = r = 0,88, apreciem ca exista o legatura liniara, puternica si directa intre cele doua variabile.
Testarea semnificatiei raportului de corelatie
- se
stabileste ipoteza nula ![]() (raportul de
corelatie al colectivitatii din care s-a extras esantionul
de 15 angajati, nu difera semnificativ de zero, deci nu este semnificativ statistic);
(raportul de
corelatie al colectivitatii din care s-a extras esantionul
de 15 angajati, nu difera semnificativ de zero, deci nu este semnificativ statistic);
- se
stabileste ipoteza alternativa ![]() ( raportul de corelatie al colectivitatii din care
s-a extras esantionul de 15 angajati, difera semnificativ de
zero, deci este semnificativ
statistic);
( raportul de corelatie al colectivitatii din care
s-a extras esantionul de 15 angajati, difera semnificativ de
zero, deci este semnificativ
statistic);
Stiind
ca pragul de semnificatie este ![]() si
si ![]() (exista un singur factor de influenta) se
stabileste:
(exista un singur factor de influenta) se
stabileste:
valoarea
critica: ![]()
regiunea
de respingere: daca ![]() , atunci H0 se respinge
, atunci H0 se respinge
Determinarea
statisticii testului (![]() ) are la baza relatia:
) are la baza relatia:
![]()
Concluzie:
Deoarece![]() , atunci
, atunci ![]() se respinge, deci
se respinge, deci ![]() se accepta, ceea
ce inseamna ca raportul de corelatie al colectivitatii
din care s-a extras esantionul de 15 angajati, difera
semnificativ de zero, deci este
semnificativ statistic.
se accepta, ceea
ce inseamna ca raportul de corelatie al colectivitatii
din care s-a extras esantionul de 15 angajati, difera
semnificativ de zero, deci este
semnificativ statistic.
Rezolvarea punctului e) al aplicatiei cu ajutorul programului informatic EXCEL
Se selecteaza din meniul principal optiunea Tools -- Data Analysis; la selectarea optiunii Regression, dupa OK, apare o fereastra in care se va completa astfel:
la Input Y Range: $B$1:$B$16
la Input X Range: $A$1:$A$16
se bifeaza Labels
se activeaza Output Range si se selecteaza o celula (exemplu: $D$1), unde vor apare tabele cu rezultate, printre care se regaseste si tabelul SUMMARY OUTPUT:
|
|
SUMMARY OUTPUT
|
Regression Statistics
|
Multiple R
|
0.883621
|
R Square
|
0.780786
|
Adjusted R Square
|
0.763923
|
Standard Error
|
1.311483
|
Observations
|
15.000000 | ||
Prezentarea detaliata a elementelor rezultate prin aplicarea programului EXCEL:
Tabel 1 -----SUMMARY OUTPUT
Multiple R
Raportul de corelatie (R)
0.883621
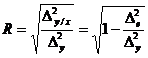
R Square
Coeficientul
(gradul ) de determinatie ![]()
0.780786
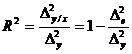
Adjusted R Square
Valoarea ajustata a coeficientului de determinatie
0.763923
![]()
Standard Error
Abaterea medie patratica a erorilor in esantion
1.311483

Observations
Numarul observatiilor = volumul esantionului (n)
15
Interpretare rezultate din tabelul SUMMARY OUTPUT
f) Realizarea unei previzionari punctuale presupune pornirea de la estimarea punctuala:
![]() polite
polite
Estimarea pe interval de incredere va fi:
![]()
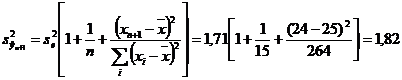 T
T ![]()
![]()
Valoarea tabelata a testului fiind ![]() se inlocuieste si se obtine:
se inlocuieste si se obtine:
![]()
![]()
Intervalul de incredere pentru numarul de polite incheiate este:
![]()
Rezolvarea problemei cu ajutorul programului informatic EXCEL
Se selecteaza din meniul principal optiunea Tools, apoi Data Analysis.
In continuare se parcurg etapele:
Regression - OK si se deschide o fereastra
la Input Y Range: $B$1:$B$16
la Input X Range: $A$1:$A$16
se bifeaza Labels
se activeaza Output Range si se selecteaza o celula (exemplu: $D$1), unde vor apare tabele cu rezultate
se bifeaza: Reziduals, Standardized Reziduals, Rezidual Plots, Line Fit Plots, Normal Probability Plots
si se obtin urmatoarele rezultate:
|
|
SUMMARY OUTPUT
|
|
|
|
|
|
Regression Statistics
|
|
|
|
|
|
Multiple R
|
0.883621
|
|
|
|
|
|
R Square
|
0.780786
|
|
|
|
|
|
Adjusted R Square
|
0.763923
|
|
|
|
|
|
Standard Error
|
1.311483
|
|
|
|
|
|
Observations
|
15.000000
|
|
|
|
|
|
ANOVA
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Significance F
|
Regression
|
1.000000
|
79.640152
|
79.640152
|
46.302727
|
0.000013
|
Residual
|
13.000000
|
22.359848
|
1.719988
|
|
|
|
Total
|
14.000000
|
102.000000
|
|
|
|
|
|
Coefficients
|
Standard Error
|
t Stat
|
P-value
|
Lower 95%
|
Upper 95%
|
Intercept
|
-1.731061
|
2.046120
|
-0.846021
|
0.412843
|
-6.151434
|
2.689313
|
X Variable 1
|
0.549242
|
0.080716
|
6.804611
|
0.000013
|
0.374866
|
0.723619
|
RESIDUAL OUTPUT
|
|
|
|
|
|
Observation
|
Predicted Y
|
Residuals
|
|
|
|
|
1.000000
|
12.000000
|
-2.000000
|
|
|
|
|
2.000000
|
10.901515
|
0.098485
|
|
|
|
|
3.000000
|
14.746212
|
-0.746212
|
|
|
|
|
4.000000
|
12.000000
|
0.000000
|
|
|
|
|
5.000000
|
9.253788
|
-1.253788
|
|
|
|
|
6.000000
|
16.393939
|
1.606061
|
|
|
|
|
7.000000
|
8.155303
|
0.844697
|
|
|
|
|
8.000000
|
9.803030
|
0.196970
|
|
|
|
|
9.000000
|
10.352273
|
-0.352273
|
|
|
|
|
10.000000
|
14.746212
|
0.253788
|
|
|
|
|
11.000000
|
12.549242
|
-1.549242
|
|
|
|
|
12.000000
|
12.549242
|
2.450758
|
|
|
|
|
13.000000
|
13.098485
|
-1.098485
|
|
|
|
|
14.000000
|
14.196970
|
-0.196970
|
|
|
|
|
15.000000
|
9.253788
|
1.746212
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||