Elemente de algebra booleana

Elemente de algebra booleana

Fisa de documentare 1 Proprietatile algebrei booleene. Functii booleene

In algebra booleana (logica) exista doua operatii: suma logica, simbolizata "+" ( se citeste SAU) si produsul logic, simbolizat "*" (se citeste SI).

 Proprietatile operatiilor din algebra booleana

• Comutativitatea

x + y = y + x

x * y = y * x

• Asociativitatea

( x + y )+z = x + ( y + z )

( x * y ) * z = x * ( y * z )

Distributivitatea

x *(y + z) = x * y + x * z

x+( y*z ) = ( x+y) * (x+z)

Algebra booleana contine numai doua elemente: 0 si 1, care sunt si elementele neutre ale operatiilor.

 Fiecarui element x din algebra i se asociaza un element numit inversul elementului x.

Cu fiecare element x din algebra si inversul sau se pot scrie doua relatii cunoscute sub numele de principii:

x + = 1, principiul tertului exclus

x * = 0 principiul contradictiei

Operatiile algebrei booleene si elementul invers au corespondent in electronica.

Tab.1 Denumirile si notatiile folosite in electronica pentru operatiile din algebra booleeana si pentru elementul invers

Algebra booleana este guvernata de un set de legi, principii si teoreme care constituie reguli de calcul in prelucrarea expresiilor logice.

Reguli de calcul in algebra booleana

• Principiul dublei negatii (Dubla negatie conduce la afirmatie)

• Legile de idempotenta

x + x + .+ x = x

x * x * * x = x

• Legile de absorbtie

x * ( x + y ) = x

x + x * y = x

• Legile lui 1 si 0

x + 0 = x             x + 1 = 1

x * 0 = 0            x * 1 = x

• Teoremele  lui De Morgan

= ;

=

Functiile din algebra booleana se numesc functii booleene sau functii logice.

O functie booleana (logica) este o functie de n variabile cu proprietatea ca atat variabilele cat si functia nu pot lua decat doua valori distincte, 0 sau 1.

Domeniul de definitie al unei functii logice de n variabile cuprinde 2ⁿ puncte, corespunzatoare tot atator combinatii distincte posibile care se pot realiza cu valorile variabilelor sale , care nu pot fi decat doua, 0 sau 1.

Domeniul in care functia ia valori este format din doua elemente: .

Functiile cele mai simple de una sau doua variabile, descrise prin suma logica, produs logic si/sau operatia de inversare se numesc functii elementare.

Tab. 2 Functii logice elementare

Se pot folosi diverse forme de exprimare a functiilor logice, din care trebuie sa rezulte ce valoare ia functia pentru toate punctele domeniului sau de definitie. Alegerea unei anumite forme de exprimare a functiei logice  depinde in mare parte de natura aplicatiei.

Forme de exprimare a functiilor logice

• Tabelul de adevar
• Forma canonica
• Diagrama Veitch-Karnaugh

Tabelul de adevar stabileste intr-un tabel corespondenta dintre valoarea de adevar a functiei logice si valorile de adevar ale variabilelor sale in toate punctele domeniului de definitie.

Exemplu:

Fig. 1 Functiile SAU si SAU EXCLUSIV reprezentate in tabel de adevar

Forma canonica este o reprezentare a functiei logice in care aceasta se scrie fie ca o suma de produse, fie ca un produs de sume.

Forma canonica in care functia se scrie ca o suma de termeni de tip produs se numeste forma canonica normala disjunctiva (f.c.n.d.).

Termenii produs (P) din f.c.n.d. se scriu pentru punctele din domeniul de definitie in care functia ia valoarea 1 ca produsul tuturor variabilelor acesteia, astfel: variabilele care au valoarea 0 se scriu negate, iar celelalte se scriu asa cum sunt. Ei se mai numesc si termeni minimali.

Exemplu:

Pentru o functie de 3 variabile, f(A,B,C), termenul P₆

Pentru o functie de 4 variabile, f(A,B,C,D), termenul P₁₂

Forma canonica in care functia se scrie ca un produs de termeni de tip suma se numeste forma canonica normala conjunctiva (f.c.n.c.).

Termenii suma (S) din f.c.n.c. se scriu pentru punctele din domeniul de definitie in care functia ia valoarea 0 ca suma tuturor variabilelor acesteia, astfel: variabilele care au valoarea 1 se scriu negate, iar celelalte se scriu asa cum sunt. Ei se mai numesc si termeni maximali.

Exemplu:

Pentru o functie de 3 variabile, f(A,B,C), termenul S₆

Pentru o functie de 4 variabile, f(A,B,C,D), termenul S₁₂

Diagrama Veitch-Karnaugh este o reprezentare grafica a formei canonice normale disjunctive.

Fiecare termen minimal din f.c.n.d. este reprezentat printr-o celula, celulele fiind asezate astfel incat doua celule alaturate sa reprezinte termeni minimali ce difera prin valoarea unei singure variabile.

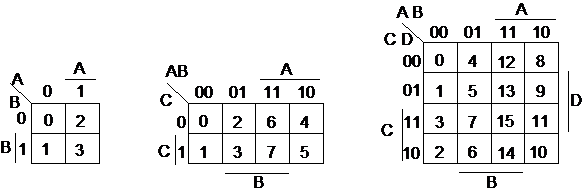
a) b) c)

Fig. 2 Ordinea termenilor minimali in diagrama Veitch-Karnaugh pentru functii

a) de 2 variabile ; b) de 3 variabile ; c) de 4 variabile

Diagrama se construieste introducand un 1 in celulele care reprezinta termenii din forma canonica normala disjunctiva a functiei si un 0 in restul celulelor.

Exemplu:

Fig. 3 Diagrama Veitch-Karnaugh asociata functiei f = P₀ + P₁ + P₄ + P₆  + P₇

Minimizarea este procedeul de obtinere a formei elementare (minime, simplificate) pentru o functie logica data in forma neelementara

Ea este obligatorie in implementarea functiilor logice cu anumite tipuri de circuite, deoarece intre gradul de complexitate al functiei si cel al circuitului care o descrie exista o stransa legatura.

Minimizarea se poate realiza prin :

• metoda analitica
• metoda diagramelor Veitch - Karnaugh

Minimizarea prin metoda analitica se realizeaza prin aplicarea regulilor de calcul din algebra booleana, operatie de multe ori dificila in cazul functiilor de mai multe variabile.

Minimizarea prin metoda diagramelor Veitch - Karnaugh presupune aplicarea regulilor de calcul ale algebrei booleene (distributivitatea si tertul exclus) pe reprezentarea functiei in diagrama Veitch - Karnaugh.

Termenii minimali din doua celule adiacente sunt identici cu exceptia unei singure variabile care intr-o celula apare complementata, iar in celula alaturata, necomplementata. Daca termenilor minimali din doua celule vecine li se aplica proprietatea de distributivitate si principiul tertului exclus, se elimina variabila care isi schimba valoarea. Pe diagrama Karnaugh acest lucru inseamna ca se scriu variabilele comune celor doua celule invecinate. Daca grupul de doua celule vecine este vecin la randul sau cu un alt grup de doua celule vecine, acestea se pot uni intr-un grup de patru celule vecine, ceea ce permite eliminarea a doua variabile.

Fiecare celula ocupata cu unitati trebuie sa faca parte cel putin dintr-o grupare, dar poate fi inclusa si in mai multe grupari, daca acest lucru contribuie la o minimizare eficienta.

Simplificarea este maxima atunci cand unitatile din diagrama sunt incluse intr-un numar cat mai mic de grupari, fiecare dintre acestea continand un numar maxim de unitati.

Pentru a se aplica succesiv proprietatea de distributivitate si principiul tertului exclus, numarul unitatilor dintr-o grupa trebuie sa fie o putere intreaga a lui 2 (doua, patru sau opt unitati).

Exemplu:

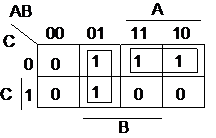
Fig. 4 Gruparea termenilor minimali pentru o functie F(A,B,C)

Gruparea celulelor care contin constituentii unitatii P₂ si P₃ conduce la expresia , iar gruparea celulelor vecine care contin constituentii unitatii P₄ si P₆ conduce la expresia . Forma minimizata a functiei se obtine ca suma logica a celor doua expresii:

F = +

Activitatea de invatare 1 Reguli de calcul in algebra booleana

Competenta:

Implementeaza functii binare simple cu circuite integrate logice

Obiective vizate:

sa identifici operatiile algebrei booleene

sa precizezi proprietatile operatiilor din algebra booleana

sa folosesti corect in aplicatii regulile de calcul din algebra booleana

Continutul: Reguli de calcul din algebra booleana

Obiectivul: Aceasta activitate va va ajuta sa folositi corect regulile de calcul in algebra booleana.

Enunt: Rezolvati sarcina care va revine prin rostogolirea aleatoare a cubului:

Descrie legile de idempotenta si legile lui 1 si 0

Compara legile absorbtiei cu proprietatea de distributivitate

Analizeaza principiul tertului exclus si principiul contradictiei

Asociaza intr-un tabel operatiile algebrei booleene si elementul invers cu denumirile si notatiile folosite in electronica

Aplica teoremele lui De Morgan pentru a demonstra egalitatea:

Argumenteaza principiul dublei negatii