Probleme distractive si sofisme matematice

Probleme distractive si sofisme matematice

Referatul este destinat prezentarii unor probleme distractive si sofisme matematice, in care pot fi descoperite proprietati surprinzatoare - pe cat de simple, pe atat de fermecatoare - ale unor concepte, relatii sau operatii matematice. Motivul pentru care am fost indemnati sa le prezentam este adevarul ca gandirea creatoare care se daruieste unor astfel de subiecte este de aceeasi natura cu tipul de gandire care conduce la descoperirea matematica, stiintifica - aceasta initiere in descoperire fiind un deziderat meritoriu inscris in sarcinile scolii de azi.

1. Calatorie temerara.

Doi baieti se gasesc la o distanta de 10 metri unul de altul, privind in sensuri opuse: unul catre est, celalalt catre vest. Ei se hotarasc sa faca ocolul Pamantului, pornind fiecare, in acelasi timp, in directia in care sunt indreptati. Ce distanta au de parcurs pana la intalnirea lor, admitand ca tinerii se aflau pe paralela terestra 45

R. Cei 10 m, caci baietii erau asezati fata-n fata.

2. Pescuit cu ghinion.

Un pescar amator - istet la matematica - se inapoia odata de la pescuit. Vazandu-l cam posomorat, fetita sa, Mirela, i-a iesit nerabdatoare in cale si   l-a intrebat:

- De ce esti suparat, tata?

- Cum sa nu fiu, ii raspunse el, cand stiu cati pesti am prins de asta data: 6 fara cap, 9 fara coada si 8 pe jumatate !

Cati pesti a prins acest sugubat pescar?

R. Din cele spuse de pescar reiese ca n-a fost prins nici un peste, pentru ca daca la cifrele 6, 9, 8 se inlatura "capul", "coada", respectiv, una dintre "jumatati", ramane mereu 0 (zero).

3. O socoteala ciudata.

Se poate arata ca: 45 - 45 = 45 (!)

Considerand egalitatea evidenta:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45,

diferenta 45 - 45 se scrie:

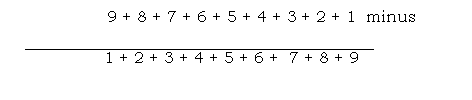
adica tot 45; bineinteles, scaderea s-a efectuat, cum scrie la carte, de la dreapta la stanga, iar cand numarul indicat de cifra scazatorului depaseste pe cel corespunzator de la descazut, s-a facut imprumut de la numarul indicat de cifra anterioara de la descazut ...

Asa sa fie oare?

R: Afirmatia paradoxala este cauzata de o eroare: acel imprumut de la numarul indicat de cifra anterioara a descazutului deoarece, asa cum sunt scrise, nu reprezinta cifre de ordin imediat superior intr-un numar scris in sistemul de numeratie zecimal, ci reprezinta doar simple unitati.

4. Pantofii si etatea.

La o sedinta a clubului "Micii matematicieni", Catalin a facut o mare senzatie, reusind sa ghiceasca varsta oricui dupa ... numarul ce-l poarta la pantofi. Procedeul sau este acesta: cere persoanei interesate sa scrie numarul de la pantofi (acesta trebuind sa fie un numar natural), sa-l dubleze, apoi sa adauge pe 35, iar rezultatul sa-l inmulteasca cu 50 si la produsul obtinut sa adauge numarul 241 (numarul acesta se va mari, an de an, cu o unitate; astfel se va folosi 242 in 1992, apoi 243 in 1993 s.a.m.d.) in fine, din suma rezultata sa scada anul nasterii. Solicitand sa i se spuna doar ultimul rezultat (sa presupunem, ca exemplu, 4261), Catalin declara: la pantofi purtati numarul 42 si aveti 61 de ani !

Puteti dezvalui secretul rationamentului sau?

R. Insemnand cu x numarul (natural) purtat la pantofi, suma dintre dublul acestuia si 35 inmultita cu 50 da:

(2x + 35) ^. 50 = 100x + 1750;

adunand, in continuare, la acest rezultat pe 241 (numarul care trebuie corelat mereu cu anul curent, ca diferenta dintre acesta si numarul ivit 1750), apoi scazand anul nasterii - pe care-l putem scrie ca diferenta dintre anul curent si varsta v - se obtine:

100x + 1750 + 241 - (1991 - v) =

= 100x + 1991 - 1991 + v = 100x + v.

Tinand cont ca numarul de la pantofi, ca si varsta, se exprima indeobste prin numere de cate doua cifre, numarul obtinut va avea patru cifre; primele doua cifre dau numarul de la pantofi, iar ultimele doua - etatea.

(Nota. Daca varsta celui interogat nu este implinita pana la data cand se fac aceste calcule, atunci din numarul corespunzator ei se scade o unitate).

5. Problema cu confidente.

Un profesor, trebuind sa dea un exemplu de polinom cu coeficienti intregi, , a facut in acelasi timp o confidenta elevilor: "Azi e ziua de nastere a fiicei mele. Daca dam lui X valoarea m egala cu a varstei ei atunci:

p(m) = m.

Precizez ca:

p(0) = n.

si n este un numar prim mai mare decat m.

Aflati pe baza acestor date, varsta fiicei mele si redati un polinom ca cel la care m-am gandit".

R Retinand faptul ca:

p(0) = n,

se intrezareste ca polinomul este de forma:

p(X) = X q(X) + n..

(unde q este un polinom cu coeficienti intregi). Atunci:

p(m) = mq(m) + n = m.

ceea ce denota ca m divide pe n [intrucat m = p(m) divide suma mq(m) + n si unul dintre termenii ei, mq(m)], si, cum n este numar prim, rezulta ca m = 1 (dat fiind ca un numar prim admite ca divizori pe el insusi si pe 1, iar m<n).

Deci varsta fiicei profesorului este 1 an, iar unul din infinitatea de polinoame, la care se poate gandi, este:

p(X) = X² - 2X + 2.

6. Imaginar sau real

Pentru a curma tacerea si (de ce nu !) chiar plictiseala tovarasilor de drum din compartimentul vagonului unde isi avea locul, Dan recurse la cateva probleme distractive, iar una dintre acestea o si schita pe o margine de ziar, astfel:

Se stie ca:

i⁴ = 1

(unde prin i s-a notat, conform uzantei,

Logaritmand ambele parti ale egalitatii, se obtine:

lg i⁴ = lg 1

sau:

4 lg i = lg 1 = 0

Deci:

lg i = lg 1,

de unde:

i = 1

Asadar, unitatea fiind imaginara, toate numerele formate cu ea ar fi imaginare . .

Desigur, avem dubiu asupra acestui fapt cauzat de o eroare; care-i aceasta?

R: Aici s-a operat cu logaritmul unui numar complex, care nu este definit ca in cazul numerelor reale pozitive.

Totusi, daca din:

4 lg i = lg 1

s-ar fi scris:

,

intrucat una dintre radacinile de ordinul patru al unitatii este i, aceste ultime egalitati pot exprima un adevar.