Calculul combinarilor

Calculul combinarilor

Atat in domeniul matematicii cat si in cel al informaticii se gasesc adesea probleme care folosesc notiuni de combinatorica. In cazul optimizarii unei astfel de probleme, ne punem  intrebarea 'cum calculam mai repede?'. In urmatoarele randuri voi prezenta raspunsul meu la aceasta intrebare.

Am folosit 3 programe distincte pentru a calcula pe care apoi le-am testat pentru diferite valori ale lui n si k. Pentru ca platforma Pascal produsa de Borland nu suporta lucrul cu valori intregi peste 2³¹ (longint), programele au fost compilate cu Free Pascal 0.9.2, pentru ca in acesta se poate folosi tipul de date pe 64 biti qword (numere pozitive pana la 2⁶⁴, cu o lungime de aproximativ 20 de cifre). Unul din procedeele de optimizare a programelor a fost formula combinarilor complementare: , adica pentru orice k > (n div 2) am calculat . Astfel, pentru un n natural, testul e maximal numai daca k = n div 2.

Primul program se bazeaza pe formula combinarilor, . Aceasta include calculul unor valori foarte mari si apoi impartirea lor. Insa, inainte de a efectua inmultirile, formula se poate simplifica: in loc sa calculeze n!, calculeaza numai produsul elementelor de la n-k+1 la n, apoi imparte la k!. Astfel se poate calcula pentru valori mai mari ale lui n. De exemplu, 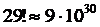, mai mult decat poate stoca qword, dar prin simplificari (k_max = 14), produsul numerelor de la 15 la 29 are 20 de cifre si poate fi retinut in qword. La testele de viteza, programul a fost eficient: pentru valori ale lui n cuprinse intre 10 si 20 si k = n div 2, timpul de executie a fost de 15-25ms, iar la valoarea maxima (n = 29, k = 14) nu a trecut de 30ms.

Al doilea program consta in calcularea combinarilor cu o formula recurenta: . Am folosit o procedura recursiva si asta implica un timp de executie considerabil, in ciuda optimizarilor facute. Pentru n20 si k = n div 2 programul a rulat in mai putin de 40ms, insa pentru 23n25 timpul de executie a ajuns la 100-140ms, iar pentru n=29 si k=14, 1sec 780ms. Spre deosebire de primul program, acesta poate calcula valoarea lui pentru n>29 insa timpul de executie devine mult prea mare. De exemplu, pentru n = 32 si k = 16, afisarea rezultatului a durat aproximativ 13sec.

Cu formula de recurenta avem posibilitatea de a implementa generarea triunghiului lui Pascal cu o matrice patratica de ordin n, insa pentru optimizare se pot folosi 2 vectori sau o matrice n2. Pentru n29 si k = n div 2, timpul de executie s-a incadrat in 30-40ms, dar valoarea maxima pe care o poate lua n este 68 (k = 34), altfel ar depasi 20 de cifre. In cazul testului cu n = 68 si k = 34, timpul de executie a fost tot 40ms.

Se observa ca cea mai rapida metoda de generare ramane construirea triunghiului lui Pascal, cu toate ca pe seturi mici de date se obtine un rezultat mai bun prin calcul direct.

Sistemul de evaluare a rulat pe un calculator cu procesor AMD Athlon XP Barthon 2500+, 768MB DDRAM. Sistemul de operare este Windows XP Professional SP2.