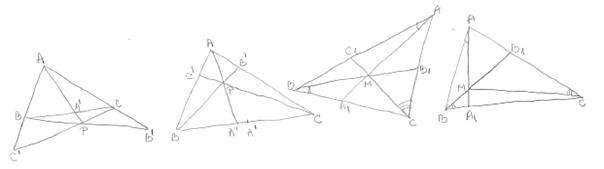
|
|
|
TEOREMA LUI CEVA
Se
considera un triunghi ABC si punctele 
, 
, 
. Daca dreptele 
, 
si 
sunt concurente
atunci:
(*) 
.
Demonstratie:
Fie 
.
Aplicam teorema lui Menelaus
pentru triunghiul 
si punctele
coliniare 
. Rezulta: 
.
Aplicam apoi teorema lui
Menelaus pentru triunghiul 
si punctele
coliniare 
. Rezulta: 
.
Inmultind ultimele doua
relatii se obtine .
(Vectorial): A, B, C necoliniare si 
astfel incat 
, 
si 
.
Sa
se arate ca , si sunt concurente
daca si numai daca 
.
Demonstratie:
Orice 
, 
sa
aratam ca sunt coliniare.
coplanare, unde 
.
, 
In triunghiul aplicam teorema
lui Menelaus si 
;
;
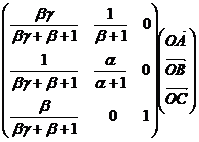= 0 
adica
Reciproca teoremei lui Ceva. Fie ABC un triunghi si punctele , , . Daca:
,
atunci dreptele , si sunt concurente.
Demonstratie:
Fie 
si fie 
Se aplica teorema lui Ceva
pentru triunghiul ABC si dreptele concurente 
si .
Rezulta: 
;
Din ultima egalitate si din relatia data in enunt se obtine:
. Deoarece 
si 
sunt puncte interioare
segmentului (BC) se obtine 
.
Observatie: Reciproca teoremei lui Ceva este
adevarata si in cazul in care unul din punctele 
se gaseste
pe o latura a triunghiului de exemplu apartine lui
(BC), iar celelalte doua puncte 
apartine dreptei
AC, 
apartine dreptei
AB si verifica conditia nu este paralel cu .
Forma trigonometrica a relatiei lui Ceva.
Fie triunghiul ABC si fie cevienele 
concurente in M. (
. Se noteaza 
si 
.
Din teorema sinusurilor in triunghiul AMB rezulta:
. Analog 
si 
.
Prin inmultirea lor se obtine:
(*) 
(relatia lui Ceva).
Reciproc, fie 
astfel incat sa
fie satisfacuta relatia (*), unde 
si 
.
Se demonsteaza ca
dreptele sunt concurente.
Se presupune ca unghiul ACB
este ascutit. Fie M punctul de intersectie a cevienelor 
si fie 
masura unghiului
ACM. Se va demonstra ca 
.
Deoarece cevienele AM, BM, CM sunt concurente rezulta relatia:
) 
.
Din (*) si (* ) se obtine: 
Se noteaza valoarea acestui
raport cu t. Deoarece unghiul ACB este unghi ascutit este suficient
sa se demonstreze ca ecuatia 
are solutie
unica 
.
Cum aceasta ecuatie are
obligatoriu solutia rezulta . Deci problema s-a redus la a arata ca
ecuatia are solutie in intervalul 
. Pentru aceasta se efectueaza calculele necesare
si se obtine:
t sin C cos x - (t cos C + 1) sin x = 0
Rezulta: 
. Dar 
, deci ecuatia considerata are solutie
unica ce apartine intervalului si cum era de asemenea
solutie cu aceasta proprietate rezulta , deci dreptele sunt concurente.
