
|
|
|
FUNCTII
Notiunea de functie
Vom trece succint in revista elementele teoretice, studiate in anul precedent, legate de conceptul de functie.
Definitie:
Fie doua multimi nevide A si B. Spunem ca am definit o
functie pe multimea A cu valori in multimea B daca
printr-un procedeu oarecare facem ca fiecarui
element ![]() sa-i
corespunda un singur element
sa-i
corespunda un singur element ![]()
O
functie definita pe A cu valori in B se noteaza ![]() sau
sau ![]() . Uneori o functie se noteaza simbolic
. Uneori o functie se noteaza simbolic ![]() ,
, ![]() , unde y este imaginea elementului x din A prin functia
f.
, unde y este imaginea elementului x din A prin functia
f.
In loc de functie se utilizeaza si termenul de aplicatie.
Trei elemente definesc o functie:
O functie ![]() se numeste numerica daca
se numeste numerica daca ![]() .
.
Graficul unei functii
Fie ![]() o functie.
o functie.
Definitie: Se numeste graficul functiei f multimea de cupluri.
![]()
Este usor de vazut ca ![]()
Daca f este o functie numerica,
atunci![]() .
.
Cum ![]() se poate reprezenta
geometric prin planul raportat la un reper cartezian, inseamna ca
graficul unei functii numerice se reprezinta geometric printr-o
submultime a planului. Numim aceasta submultime reprezentarea
geometrica a graficului functiei f sau pe scurt (prin abuz de limbaj)
graficul functiei f.
se poate reprezenta
geometric prin planul raportat la un reper cartezian, inseamna ca
graficul unei functii numerice se reprezinta geometric printr-o
submultime a planului. Numim aceasta submultime reprezentarea
geometrica a graficului functiei f sau pe scurt (prin abuz de limbaj)
graficul functiei f.
Functii egale
Definitie: Fie![]() doua functii.
doua functii.
Spunem ca functiile f,g sunt egale (si scriem f=g) daca:
1) A=C (domeniile lor sunt egale);
2) B=D (codomeniile lor sunt egale);
3)
![]() (punctual functiile
coincid)
(punctual functiile
coincid)
Operatii cu functii
Fie A o multime nevida si ![]() , doua functii reale.
, doua functii reale.
Definitie:
1)
Functia ![]() se numeste suma
dintre functia f si functia g.
se numeste suma
dintre functia f si functia g.
2)
Functia ![]() definita prin
definita prin ![]() se numeste
produsul functiilor f,g.
se numeste
produsul functiilor f,g.
3)
Functia ![]() definita prin
definita prin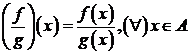 , unde
, unde ![]() se numeste catul
dintre functia f si functia g.
se numeste catul
dintre functia f si functia g.
Fie acum ![]() si
si ![]() .
.
Definitie: Functia ![]() definita prin
definita prin ![]() se numeste
compusa lui g cu f.
se numeste
compusa lui g cu f.
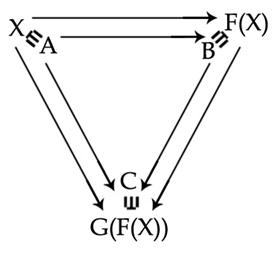
Compunerea functiilor este asociativa, adica ![]() astfel incat sa
aiba sens compunerea lor.
astfel incat sa
aiba sens compunerea lor.
In
general compunerea functiilor nu este comutativa, adica nu
pentru orice f,g doua functii pentru care are sens ![]() si
si ![]() ,
, ![]() .
.
Functia identica a unei multimi
Fie A o multime.
Definitie:
Functia ![]() definita prin
definita prin ![]() , se numeste aplicatia identica a
multimii A.
, se numeste aplicatia identica a
multimii A.
Daca
![]() este o functie oarecare, atunci
este o functie oarecare, atunci ![]() , iar daca
, iar daca ![]() este o functie oarecare atunci
este o functie oarecare atunci ![]() . Daca notam
. Daca notam ![]() atunci
atunci ![]()
In
acest ultim caz spunem ca ![]() este element neutru in
raport cu operatia de compunere a functiilor din
este element neutru in
raport cu operatia de compunere a functiilor din ![]() (Rol similar jucat de
numarul 0 pentru adunarea numerelor reale sau numarul 1 pentru
operatia de inmultire a numerelor reale).
(Rol similar jucat de
numarul 0 pentru adunarea numerelor reale sau numarul 1 pentru
operatia de inmultire a numerelor reale).
Imaginea si preimaginea unei functii
Fie ![]() o functie.
o functie.
Definitie:
Se numeste imaginea functiei f multimea notata ![]() si egala cu
si egala cu ![]() Uneori in loc de
Uneori in loc de ![]() se scrie
se scrie ![]() . Se numeste preimaginea functie f multimea
notata
. Se numeste preimaginea functie f multimea
notata ![]()
Daca
![]() atunci multimea elementelor
atunci multimea elementelor ![]() care sunt imaginea prin f a cel putin unui element x din
care sunt imaginea prin f a cel putin unui element x din
![]() se numeste
imaginea multimii
se numeste
imaginea multimii ![]() prin f si se
noteaza cu
prin f si se
noteaza cu ![]()
Deci
![]() .
.
Daca
![]() , atunci notam prin
, atunci notam prin ![]() (citim: f la minus 1 din
(citim: f la minus 1 din ![]() ) multimea
) multimea ![]() care se numeste imaginea reciproca a multimii
care se numeste imaginea reciproca a multimii ![]() prin f.
prin f.
Prezentam in continuare imaginile unor functii:
E: Fie ![]() Sa se determine
Sa se determine ![]() .
.
R. Avem ![]()
![]()
Din ![]() rezulta
rezulta ![]() si deci
si deci ![]() .
.
Cum ![]() Deci
Deci ![]()
Mai jos este redat graficul functiei f:
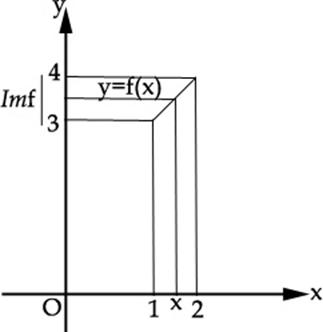
Pe axa Ox am marcat mai accentuat segmentul ![]() care este domeniul de definitie pentru functie, iar
pe axa Oy am accentuat segmentul care este
care este domeniul de definitie pentru functie, iar
pe axa Oy am accentuat segmentul care este ![]() .
.
E: Fie ![]() Sa se determine
Sa se determine ![]()
R. Fie ![]() Deci exista
Deci exista ![]() astfel incat
astfel incat ![]() , adica
, adica ![]() . De aici
. De aici ![]() si
si ![]() . Cum
. Cum ![]() se disting doua cazuri:
se disting doua cazuri:
1) ![]()
2) ![]()
Prin urmare daca ![]() atunci
atunci ![]() . Deci
. Deci ![]() . Graficul functiei este prezentat mai jos.
. Graficul functiei este prezentat mai jos.
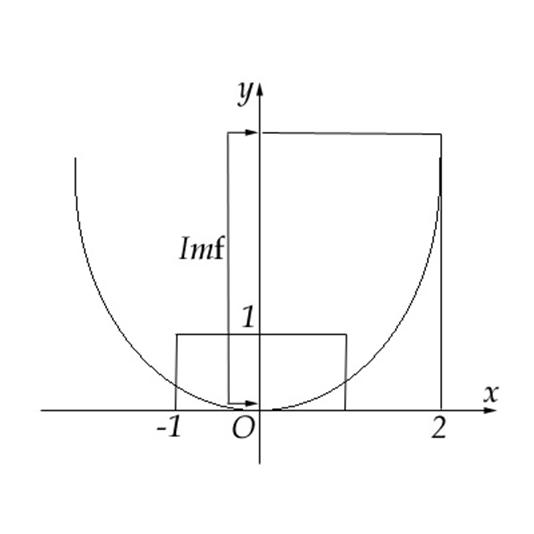
E: Se considera functia ![]() Se cere
Se cere ![]()
R. Fie ![]() Deci exista
Deci exista ![]() astfel incat
astfel incat ![]() , adica
, adica ![]() . De aici
. De aici ![]() . Cum
. Cum ![]() rezulta
rezulta ![]() . De aici si
. De aici si ![]() rezulta
rezulta![]() Asadar
Asadar ![]()
Graficul functiei este ilustrat mai jos.
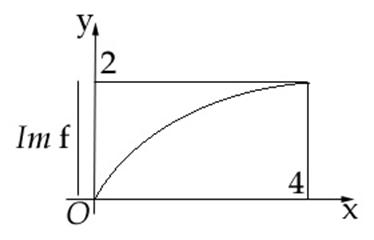
Probleme propuse
Determinati ![]() pentru urmatoarele functii:
pentru urmatoarele functii:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) 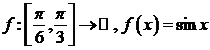
6) ![]()
7) 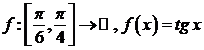
8) 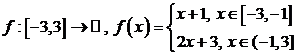
9) 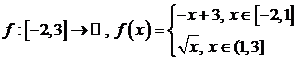
Prelungirea si restrictia unei functii
Daca ![]() si
si ![]() sunt doua
functii cu proprietatile:
sunt doua
functii cu proprietatile:
1) ![]()
2) ![]()
atunci f se numeste
prelungirea functiei g la A, in timp ce g este numita restrictia
lui f la ![]() .
.
Functii monotone
Fie ![]() , o functie de variabila reala si
, o functie de variabila reala si ![]()
Definitie:
1) Spunem ca functia f este strict crescatoare pe I daca:
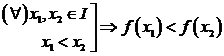
(Spunem ca functia f strict crescatoare "conserva" relatia de ordine dintre argumente si pentru valorile functiei in aceste puncte)
2) Spunem ca functia f este strict descrescatoare pe I daca:
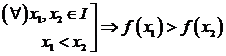
(Spunem ca functia f strict descrescatoare "schimba" relatia de ordine dintre argumente pentru valorile functiei)
O functie f strict crescatoare pe I sau strict descrescatoare pe I se numeste strict monotona pe I.
Definitie:
1) Spunem ca functia f este crescatoare pe I daca:
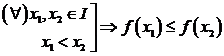
2) Spunem ca functia f este descrescatoare pe I daca:
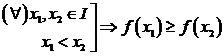
O functie f crescatoare pe I sau descrescatoare pe I se numeste monotona pe I.
Daca f este strict monotona (sau monotona) pe A (pe tot domeniul de definitie) spunem simplu ca functia f este strict monotona (sau monotona) fara a mai indica multimea.
A studia monotonia unei functii ![]() revine la a preciza
submultimile lui A pe care f este strict crescatoare (sau
crescatoare) si submultimile lui A pe care f este strict
descrescatoare (sau crescatoare).
revine la a preciza
submultimile lui A pe care f este strict crescatoare (sau
crescatoare) si submultimile lui A pe care f este strict
descrescatoare (sau crescatoare).
Pentru studiul monotoniei unei functii
numerice ![]() , s-a utilizat raportul
, s-a utilizat raportul 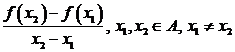 , numit raportul de variatie asociat functiei f
si argumentelor
, numit raportul de variatie asociat functiei f
si argumentelor ![]()
Diferenta ![]() se numeste
variatia argumentului, iar diferenta
se numeste
variatia argumentului, iar diferenta ![]() se numeste variatia functiei. Prin urmare
raportul de variatie asociat lui f si numerelor
se numeste variatia functiei. Prin urmare
raportul de variatie asociat lui f si numerelor ![]() este raportul dintre
variatia functiei si variatia argumentului.
este raportul dintre
variatia functiei si variatia argumentului.
Are loc urmatoarea:
Teorema: Fie![]() o functie numerica si
o functie numerica si ![]() . Atunci:
. Atunci:
1)
f este strict crescatoare (crescatoare) pe
I ![]()
![]()
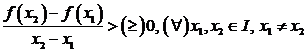
2)
f este strict descrescatoare (descrescatoare) pe
I![]()
![]()
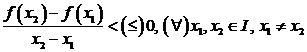
Functiile studiate anul trecut au fost (din tabelul de valori se extrag usor intervalele de monotonie: in dreapta tabelului am indicat forma graficului):
1)
Functia de
gradul intai:![]() . Daca
. Daca ![]() atunci f este strict crescatoare si am indicat
aceasta situatie in tabelul de valori astfel:
atunci f este strict crescatoare si am indicat
aceasta situatie in tabelul de valori astfel:
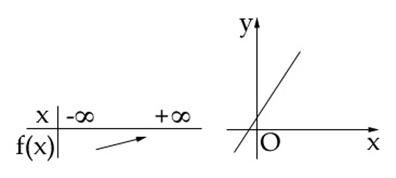
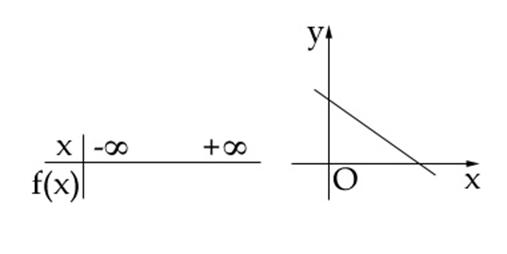
Daca ![]() atunci f este strict
descrescatoare si s-a indicat aceasta situatie in tabelul
de valori astfel:
atunci f este strict
descrescatoare si s-a indicat aceasta situatie in tabelul
de valori astfel:
2)
Functia de
gradul al doilea:![]()
![]()
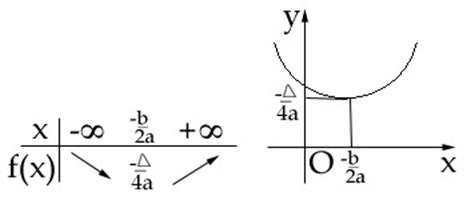
![]() . Intervalele de monotonie ale acestei functii sunt:
. Intervalele de monotonie ale acestei functii sunt: ![]() . Daca
. Daca ![]() atunci monotonia lui f este indicata in tabelul de
valori:
atunci monotonia lui f este indicata in tabelul de
valori:
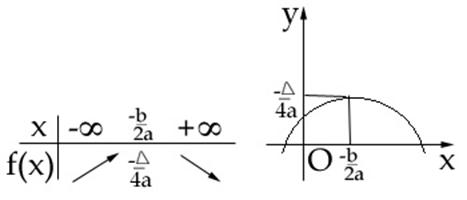
Daca ![]() atunci tabelul de valori are forma:
atunci tabelul de valori are forma:
3)
Functia
putere cu exponent natural: ![]() . Daca n este par, atunci tabelul de valori are forma:
. Daca n este par, atunci tabelul de valori are forma:
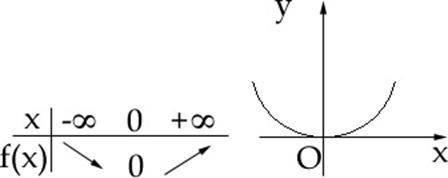
Daca n este impar, ![]() atunci tabelul de valori are forma:
atunci tabelul de valori are forma:
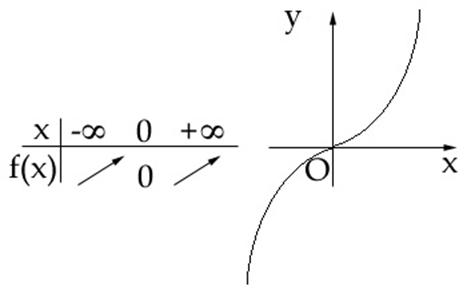
4) Functia radical de ordin n:
Daca n este par atunci functia![]() are tabelul de valori:
are tabelul de valori:
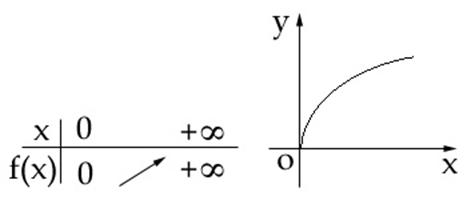
Daca n este impar atunci functia![]() are tabelul de valori:
are tabelul de valori:
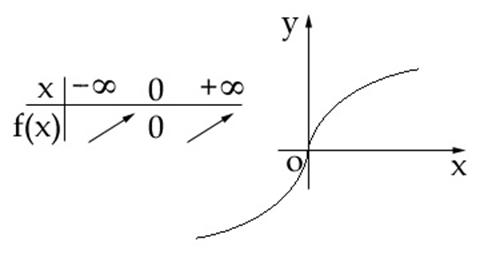
5)
Functia
sinus, notata ![]() este o functie
periodica de perioada principala
este o functie
periodica de perioada principala ![]() . Este suficient sa studiem monotonia acestei
functii pe un interval de lungimea unei perioade principale, de exemplu
. Este suficient sa studiem monotonia acestei
functii pe un interval de lungimea unei perioade principale, de exemplu ![]() .
.
Tabelul de valori este:
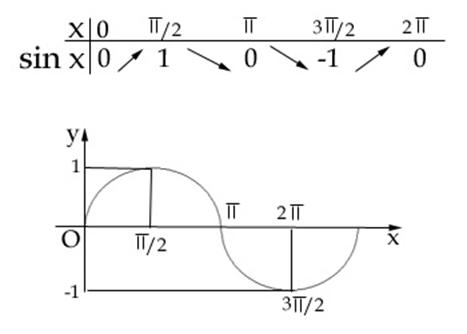
Deci functia sin este strict crescatoare pe intervalele ![]() si strict
descrescatoare pe intervalul
si strict
descrescatoare pe intervalul ![]() .
.
Monotonia functiei sin pe R se obtine adaugand la
capetele intervalelor de mai sus multiplu de perioada principala. Asadar
functia sin este strict crescatoare pe intervalele 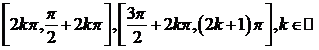 si strict descrescatoare
pe intervalele
si strict descrescatoare
pe intervalele 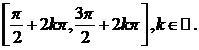
Particularizand k in fiecare din multimile de mai sus se
obtin intervale pe care functia este strict crescatoare sau
strict descrescatoare. De exemplu, pentru ![]() , functia sin este strict crescatoare pe
intervalele:
, functia sin este strict crescatoare pe
intervalele: 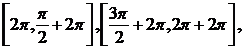 iar pe intervalul
iar pe intervalul 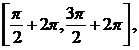 functia este strict descrescatoare.
functia este strict descrescatoare.
6)
Functia
cosinus, notata ![]() , este o functie de asemenea periodica de
perioada principala
, este o functie de asemenea periodica de
perioada principala ![]() .
.
Studiul acestei functii poate fi realizat pe ![]() .
.
Tabelul de valori este:
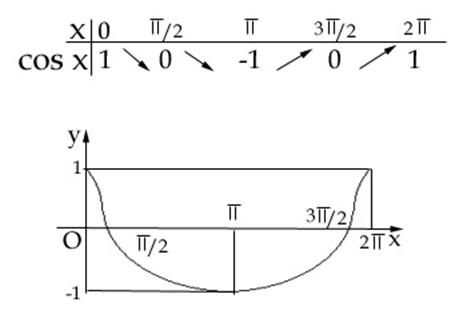
Deci functia cos este strict descrescatoare pe ![]() si strict
crescatoare pe
si strict
crescatoare pe ![]() .
.
Pentru a obtine intervalele de monotonie din R ale acestei functii se adauga la capetele intervalelor de mai sus multiplu de perioada principala.
Deci pe intervalele ![]() , functia cos este strict descrescatoare, iar pe
intervalele
, functia cos este strict descrescatoare, iar pe
intervalele![]() functia cos este strict crescatoare.
functia cos este strict crescatoare.
Prin particularizari ale lui ![]() se obtin
intervale din R pe care functia este strict crescatoare sau strict
descrescatoare.
se obtin
intervale din R pe care functia este strict crescatoare sau strict
descrescatoare.
7)
Functia
tangenta, notata ![]() este o functie
periodica de perioada principala
este o functie
periodica de perioada principala ![]() .
.
Prin urmare este suficient sa studiem comportarea functiei
pe un interval de lungimea unei perioade, de exemplu 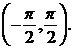
Tabelul de variatie este:
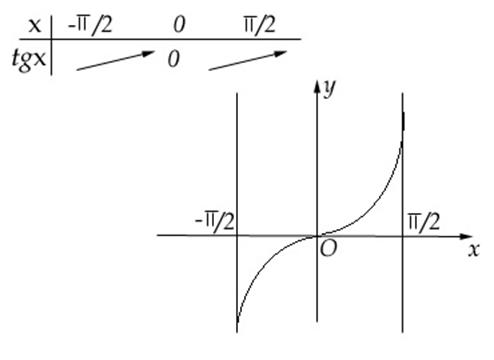
Functia ![]() este strict crescatoare pe
este strict crescatoare pe 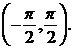
Intervalele din R pe care functia ![]() este strict crescatoare se obtin adaugand
capetelor intervalului de mai sus multiplu de perioada principlaa.
Obtinem intervalele
este strict crescatoare se obtin adaugand
capetelor intervalului de mai sus multiplu de perioada principlaa.
Obtinem intervalele ![]() .
.
8)
Functia
cotangenta, notata ![]() este o functie
periodica de perioada principala
este o functie
periodica de perioada principala ![]() .
.
Vom lua ca interval de studiu![]() . Tabelul de valori arata astfel:
. Tabelul de valori arata astfel:
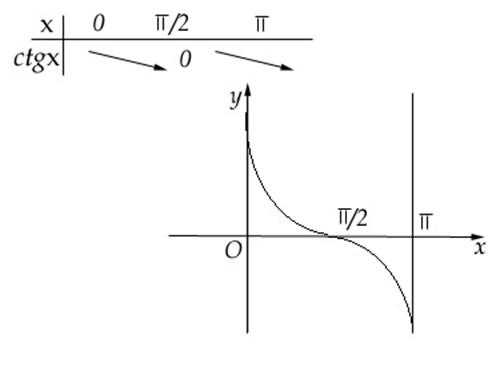
Functia ctg este strict descrescatoare pe ![]() .
.
Intervalele din R pe care functia este strict descrescatoare
sunt ![]()
O functie monotona pe o multime A ramane monotona pe orice submultime a sa.
Daca o functie![]() este strict crescatoare pe
este strict crescatoare pe ![]() si pe
si pe ![]() , nu rezulta neaparat ca f este strict
crescatoare pe R (adica pe intreaga multime).
, nu rezulta neaparat ca f este strict
crescatoare pe R (adica pe intreaga multime).
De exemplu, fie ![]() definita prin:
definita prin: 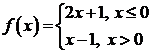
Cum functiile ![]() sunt strict
crescatoare pe R, atunci ele raman la fel si pe intervalele
sunt strict
crescatoare pe R, atunci ele raman la fel si pe intervalele ![]() si respectiv
si respectiv ![]() .
.
Deci f este strict crescatoare pe ![]() ,
, ![]() , fara a fi strict crescatoare pe R, deoarece
pentru
, fara a fi strict crescatoare pe R, deoarece
pentru ![]() avem
avem ![]() .
.
Asadar nu pentru orice ![]() rezulta
rezulta ![]() .
.
Graficul functiei f este cel din figura.
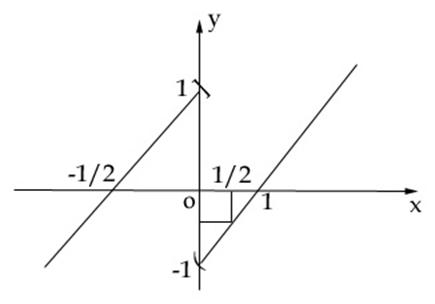
Conditia de functie strict crescatoare pe R a fost verificata pentru:
1) ![]()
2) ![]()
Mai ramane de aratat ca are loc si:
3) ![]() (evident
(evident ![]() ) sa avem
) sa avem ![]() .
.
In cazul functiei de mai sus tocmai aceasta conditie nu a avut loc.
In general pentru a arata ca o functie multiforma (cu doua forme) este strict crescatoare trebuie verificate 1,2,3 (unde in loc de zero poate fi orice numar real).
Utilizand graficul putem stabili daca functia este strict crescatoare.
Graficele de mai jos indica functii strict crescatoare.
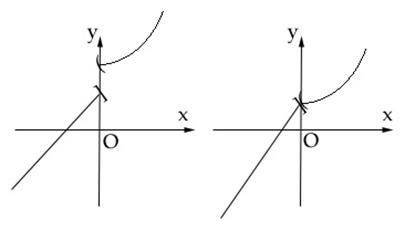
Se observa ca ambele ramuri "urca", iar ramura din dreapta trebuie sa "plece" cel putin din punctul in care se termina ramura din stanga.
Graficele de mai jos indica functii strict descrescatoare.
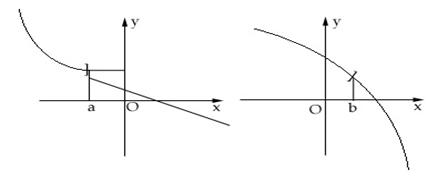
Sa observam ca ambele ramuri "coboara", iar ramura din dreapta trebuie sa "plece" cel mult din punctul in care se termina ramura din stanga.
Problema se extinde usor la functiile cu mai mult de doua ramuri.
Exercitii propuse
Stabiliti daca functia ![]() este strict
monotona pe
este strict
monotona pe ![]() , in cazurile:
, in cazurile:
1) 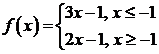
2) 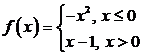
3) 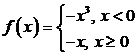
4) 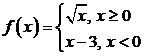
5) 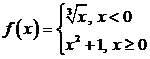
6) 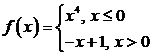
Operatii cu functii strict monotone
Fie ![]()
Teorema:
1) Daca f este strict crescatoare (strict descrescatoare) atunci (-f) este strict descrescatoare (strict crescatoare).
2) Daca f,g sunt strict crescatoare (strict descrescatoare) atunci f+g este strict crescatoare (strict descrescatoare). Suma a doua functii strict crescatoare (strict descrescatoare) este o functie strict crescatoare (strict descrescatoare).
3)
Daca f si g sunt strict crescatoare (sau
strict descrescatoare), atunci ![]() este strict crescatoare. Compunerea a doua
functii de aceeasi monotonie da o functie strict
crescatoare.
este strict crescatoare. Compunerea a doua
functii de aceeasi monotonie da o functie strict
crescatoare.
4)
Daca f si g au monotonii diferite, atunci![]() este strict descrescatoare.
este strict descrescatoare.
5)
Fie f inversabila. Daca f este strict
crescatoare (sau strict descrescatoare), atunci ![]() este strict crescatoare
(sau strict descrescatoare).
este strict crescatoare
(sau strict descrescatoare).
Demonstratie:
1)
Presupunem ca f este strict crescatoare. Sa
probam ca (-f) este strict descrescatoare. Deci sa
aratam ca: ![]()
![]() .
.
Ori ![]() , adevarat daca tinem seama ca f este
strict crescatoare.
, adevarat daca tinem seama ca f este
strict crescatoare.
2)
Fie f,g strict crescatoare. Sa aratam
ca f+g are aceeasi calitate. Fie ![]() Atunci
Atunci ![]() si
si ![]() De aici prin adunarea
acestor inegalitati rezulta
De aici prin adunarea
acestor inegalitati rezulta ![]() sau
sau ![]() .
.
Recapituland, avem ![]() care reprezinta
cerinta ca f+g sa fie strict crescatoare.
care reprezinta
cerinta ca f+g sa fie strict crescatoare.
Analog se procedeaza si in cazul functiilor strict descrescatoare.
3)
Presupunem ca f si g sunt strict
crescatoare. Fie ![]() Atunci (g strict
crescatoare)
Atunci (g strict
crescatoare) ![]() , iar din f strict crescatoare se deduce
, iar din f strict crescatoare se deduce ![]() sau
sau ![]() . Asadar
. Asadar ![]() , am obtinut
, am obtinut ![]() , ceea ce arata ca
, ceea ce arata ca ![]() este strict crescatoare.
este strict crescatoare.
Analog se procedeaza pentru functiile f si g strict descrescatoare.
4)
Fie f strict crescatoare, g strict
descrescatoare. Sa aratam ca ![]() este strict descrescatoare. Fie
este strict descrescatoare. Fie ![]() . Din g strict descrescatoare se deduce
. Din g strict descrescatoare se deduce ![]() , iar din f strict crescatoare avem:
, iar din f strict crescatoare avem: ![]() sau
sau ![]() .
.
Deci ![]() , ceea ce ne arata ca
, ceea ce ne arata ca ![]() este strict descrescatoare.
este strict descrescatoare.
5)
Fie ![]() inversabila
strict crescatoare si
inversabila
strict crescatoare si ![]() inversa. Fie
inversa. Fie ![]() si
si ![]() . Atunci exista
. Atunci exista ![]() astfel incat
astfel incat ![]() . Deci
. Deci ![]() . Cum f este strict crescatoare deducem
. Cum f este strict crescatoare deducem ![]() , adica
, adica ![]() . Asadar din
. Asadar din ![]() , adica
, adica ![]() este strict
crescatoare.
este strict
crescatoare.
Observatii:
1)
Daca ![]() si
si ![]() este strict
crescatoare (strict descrescatoare), atunci
este strict
crescatoare (strict descrescatoare), atunci ![]() este strict crescatoare (strict
descrescatoare).
este strict crescatoare (strict
descrescatoare).
2) O suma finita de functii strict crescatoare (strict descrescatoare) pe o multime este o functie strict crescatoare (strict descrescatoare) pe acea multime.
Probleme Rezolvate
Sa se stabileasca monotonia functiilor urmatoare:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
R. a) Functia f este
suma de doua functii strict crescatoare pe R, ![]() si deci este o
functie strict crescatoare.
si deci este o
functie strict crescatoare.
b) Punand ![]() , doua functii strict crescatoare pe
, doua functii strict crescatoare pe ![]() fiind suma a doua
astfel de functii.
fiind suma a doua
astfel de functii.
c) Daca ![]() functii strict crescatoare pe
functii strict crescatoare pe ![]() , atunci
, atunci ![]() fiind suma a doua
functii strict crescatoare, este de asemenea strict crescatoare
fiind suma a doua
functii strict crescatoare, este de asemenea strict crescatoare
d) Luand ![]() , functii strict crescatoare, se deduce ca
, functii strict crescatoare, se deduce ca ![]() are aceeasi
calitate.
are aceeasi
calitate.
e) In acest
caz functiile ![]() sunt strict
descrescatoare, iar
sunt strict
descrescatoare, iar ![]() este de asemenea
strict descrescatoare
este de asemenea
strict descrescatoare
f) Functiile ![]() sunt strict descrescatoare
si deci
sunt strict descrescatoare
si deci ![]() are aceeasi
proprietate pe
are aceeasi
proprietate pe ![]()
Probleme propuse
Stabiliti monotonia functiilor urmatoare:
1)
![]()
2)
![]()
3)
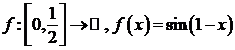
4)
![]()
5)
![]()
6)
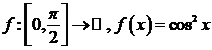
7)
![]()
8)
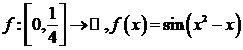
9)
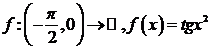
10) 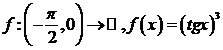
Functii convexe (si concave)
Dupa clasa functiilor monotone (crescatoare sau descrescatoare) pe o multime, trebuie subliniata clasa asa numitelor functii convexe si concave.
Atragem atentia ca abordarea riguroasa a unor concepte din acest paragraf va fi realizata in cadrul cursului de analiza matematica.
(Presupunem ca in fiecare punct al graficului se poate construi tangenta la grafic).
Incepem pregatirea acestui paragraf prin cateva remarci:
1)Fie o portiune din graficul functiei ![]() si A,B doua puncte de pe acest grafic.
Consideram coarda AB de panta
si A,B doua puncte de pe acest grafic.
Consideram coarda AB de panta ![]()
Grafic
Daca se "coboara" aceasta coarda pastrand
panta ![]() a dreptei
initiale AB, punctele A, B se vor "apropia" pe grafic din ce in ce mai
mult pana coincid in punctul T. Spunem ca dreapta devine tangenta
in punctul T la graficul functiei. In aceasta situatie graficul
este situat "deasupra" tangentei (prima figura). In a doua figura,
graficul este situat sub tangenta in T la grafic.
a dreptei
initiale AB, punctele A, B se vor "apropia" pe grafic din ce in ce mai
mult pana coincid in punctul T. Spunem ca dreapta devine tangenta
in punctul T la graficul functiei. In aceasta situatie graficul
este situat "deasupra" tangentei (prima figura). In a doua figura,
graficul este situat sub tangenta in T la grafic.
2) O functie poate fi strict crescatoare in doua moduri (figurile de mai jos).
Grafic
In figura din stanga, graficul se afla sub tangenta in fiecare punct al sau, iar in cazul figurii din dreapta, graficul se afla deasupra fiecarei tangente in fiecare punct al sau.
De asemenea o functie poate fi strict descrescatoare in doua moduri (figurile de mai jos).
Grafic
Aceleasi observatii de la functia strict crescatoare privind pozitia graficului in raport cu tangentele in punctele sale se pot face si aici.
Definitie: Fie functia
![]() I interval. Se spune
ca functia f este convexa
pe I daca
I interval. Se spune
ca functia f este convexa
pe I daca ![]() si
si ![]() avem
avem ![]() (1)
(1)
Functia f se numeste concava
pe I daca ![]() si
si ![]() avem:
avem: ![]() . (2)
. (2)
Observatii:
1) Daca in inegalitatile (1) si (2) avem inegalitate stricta se spune ca functia f este strict convexa si respectiv strict concava pe I.
2) Notiunea de
functie convexa (concava) a fost introdusa de Jensen, care
a pornit de la o relatie mai particulara decat (1) sau (2) si
anume 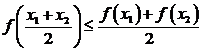 si respectiv
si respectiv 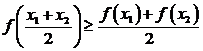 care corespunde lui
care corespunde lui ![]() .
.
Pentru functiile pe care le analizam ![]()
![]() ,
, ![]() (
(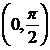 de exemplu),
de exemplu), ![]() , (
, (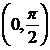 de exemplu), aceasta definitie este
echivalenta cu cea data in text.
de exemplu), aceasta definitie este
echivalenta cu cea data in text.
3) Daca f este convexa
pe I, atunci ![]() este concava pe I.
este concava pe I.
4) Daca punem ![]() , atunci
, atunci ![]() cu
cu ![]() , iar (1) si (2) se scriu:
, iar (1) si (2) se scriu: ![]() (1
(1
![]() (2
(2
Interpretare geometrica
Sa consideram punctele ![]() apartinand graficului functiei
apartinand graficului functiei ![]() , I = interval si punctul
, I = interval si punctul ![]() . Acest punct parcurge intervalul
. Acest punct parcurge intervalul ![]() cand
cand ![]() .
.
Intr-adevar trebuie sa aratam ca: ![]() .
.
Prima inegalitate se scrie echivalent ![]() evident.
evident.
Analog, a doua inegalitate devine: ![]()
![]() , adevarat deoarece
, adevarat deoarece ![]() si
si ![]()
Grafic
Dreapta AB are ecuatia (determinata de doua puncte):
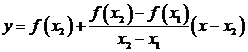
Fie punctul C de abscisa ![]() care are ordonata:
care are ordonata:
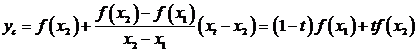
Punctul C de pe graficul
functiei are abscisa ![]() si ordonata
si ordonata ![]() . Pentru forma graficului prezentata in figura avem:
. Pentru forma graficului prezentata in figura avem:![]() sau
sau ![]() , ceea ce corespunde functiei convexe.
, ceea ce corespunde functiei convexe.
Semnificatia inegalitatii ![]() , in cazul functiei convexe este:
, in cazul functiei convexe este:
Graficul functiei convexe intre doua puncte ale graficului este situat sub coarda determinata de cele doua puncte.
- sau, daca tinem seama de remarcile prezentate la inceput -
Graficul functiei convexe este situat deasupra oricarei tangente duse intr-un punct al graficului.
Semnificatia inegalitatii ![]() , in cazul functiei concave este:
, in cazul functiei concave este:
Graficul functiei concave intre doua puncte ale graficului este situat deasupra coardei determinate de cele doua puncte.
- sau -
Graficul functiei concave este situat sub orice tangenta dusa intr-un punct al graficului.
Se mai spune despre functia convexa ca are graficul o curba convexa iar despre functia concava ca are graficul o curba concava.
Un punct al graficului in care se schimba forma convexa cu concava sau concava cu convexa se numeste punct de inflexiune al graficului.
In limbajul trivial spunem despre graficul convex, avand forma sectiunii unui vas cu gura in sus, ca "tine apa", in timp ce graficul concav "nu tine apa".
Exemple de functii studiate
1)
Functia de
gradul intai, ![]() este atat convexa cat si concava deoarece
(pentru
este atat convexa cat si concava deoarece
(pentru ![]() ) avem:
) avem: ![]()
![]()
2)
Functia de
gradul al doilea, f![]()
![]()
3)
Functia cubica,
![]() este concava pe
este concava pe ![]() si convexa pe
si convexa pe ![]() , ceea ce arata ca
, ceea ce arata ca ![]() este punct de
inflexiune pentru graficul functiei. In general
este punct de
inflexiune pentru graficul functiei. In general ![]() este concava pe
este concava pe ![]() si convexa pe
si convexa pe ![]() .
.
4)
Functia
radical de ordin 2, ![]() este concava deoarece
este concava deoarece ![]() avem:
avem: ![]()
![]()
![]()
![]() , adevarat (inegalitatea mediilor pentru doua
numere pozitive).
, adevarat (inegalitatea mediilor pentru doua
numere pozitive).
5)
Functia
radical de ordin 3,![]() este convexa pe
este convexa pe
![]() si concava pe
si concava pe ![]() Punctul
Punctul ![]() este punct de inflexiune pentru graficul functiei.
este punct de inflexiune pentru graficul functiei.
6)
Functia
sinus, ![]() . Pentru aceasta functie precizam convexitatea
pe un interval de lungimea unei perioade principale
. Pentru aceasta functie precizam convexitatea
pe un interval de lungimea unei perioade principale ![]() . Pe
. Pe ![]() functia este concava, iar pe intervalul
functia este concava, iar pe intervalul ![]() functia este convexa. Deci punctul
functia este convexa. Deci punctul ![]() este punct de inflexiune al functiei.
Pentru
este punct de inflexiune al functiei.
Pentru ![]() avem: pe intervalele
avem: pe intervalele ![]() , functia este concava, iar pe intervalele
, functia este concava, iar pe intervalele ![]() , functia este convexa. Punctele
, functia este convexa. Punctele ![]() , sunt puncte de inflexiune pentru functie.
, sunt puncte de inflexiune pentru functie.
7)
Functia
cosinus, ![]() . Pentru intervalul
. Pentru intervalul ![]() avem: pe
avem: pe ![]() , functia este concava;
pe
, functia este concava;
pe 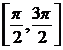 functia este convexa; pe
functia este convexa; pe 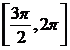 functia este concava.
functia este concava.
Deci punctele ![]() si
si ![]() sunt puncte de
inflexiune pentru functia cosinus.
sunt puncte de
inflexiune pentru functia cosinus.
Extinderea acestor rezultate pe ![]() este imediata. Din forma graficelor functiilor
este imediata. Din forma graficelor functiilor ![]() pe intervalul
pe intervalul 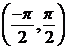 si
si ![]() pe
pe ![]() precizati
intervalele de convexitate (concavitate) si punctele de inflexiune.
precizati
intervalele de convexitate (concavitate) si punctele de inflexiune.
Observatie: Se poate demonstra prin inductie matematica
(inegalitatea lui Jensen): ![]() daca f este convexa (concava),
daca f este convexa (concava), ![]()
Probleme rezolvate
1. a) Sa se arate ca produsul dintre o functie convexa si o functie constanta pozitiva este o functie convexa.
b) Sa se arate ca o suma de functii convexe este o functie convexa.
c) Daca ![]() g convexa iar f
convexa si crescatoare, atunci
g convexa iar f
convexa si crescatoare, atunci ![]() este convexa.
este convexa.
d) Daca f si g sunt functii reciproce, atunci au loc afirmatiile:
![]() . f convexa, crescatoare
. f convexa, crescatoare ![]() g concava,
crescatoare
g concava,
crescatoare
![]() . f convexa, descrecatoare
. f convexa, descrecatoare ![]() g convexa,
descrescatoare
g convexa,
descrescatoare
e) Daca ![]() , I interval, este o functie neconstanta si
convexa, atunci f nu-si poate atinge valoarea cea mai mare in
interiorul intervalului.
, I interval, este o functie neconstanta si
convexa, atunci f nu-si poate atinge valoarea cea mai mare in
interiorul intervalului.
R.
a) Fie ![]() , I interval, f convexa si
, I interval, f convexa si ![]() . Trebuie probat ca
. Trebuie probat ca ![]() este convexa,
adica
este convexa,
adica ![]()
![]()
Cum f este convexa rezulta: ![]() .
.
Inmultind aceasta inegalitate prin ![]() se obtine
relatia dorita.
se obtine
relatia dorita.
b) Probam
afirmatia pentru doua functii convexe ![]() Fie
Fie ![]()
Scriem ca f,g sunt convexe, adica: ![]()
![]()
Adunam aceste inegalitati, membru cu membru, si obtinem:
![]() ceea ce arata
ca
ceea ce arata
ca ![]() este convexa.
este convexa.
c) Din g
convexa pe I rezulta: ![]()
![]() De aici rezulta
(f crescatoare, combinata
cu f convexa):
De aici rezulta
(f crescatoare, combinata
cu f convexa): ![]() ceea ce arata ca
ceea ce arata ca ![]() este convexa (de
observat momentul in care a intervenit faptul ca f este crescatoare - deci de retinut
ca f,g convexe nu implica
este convexa (de
observat momentul in care a intervenit faptul ca f este crescatoare - deci de retinut
ca f,g convexe nu implica ![]() convexa!).
convexa!).
d) Vom demonstra doar ![]()
Fie![]() I si J intervale din R si
I si J intervale din R si ![]() inversa lui f.
Daca f este crescatoare, atunci am vazut (la functii
monotone) ca g este crescatoare. Sa aratam ca g
este concava, adica
inversa lui f.
Daca f este crescatoare, atunci am vazut (la functii
monotone) ca g este crescatoare. Sa aratam ca g
este concava, adica ![]() .
. ![]()
Pentru ![]() exista
exista ![]() astfel incat
astfel incat ![]() Din f convexa rezulta:
Din f convexa rezulta: ![]()
Dar f este crescatoare si de aici avem: ![]() sau
sau ![]() .
.
e) Prin reducere la absurd. Presupunem ca f
isi atinge cea mai mare valoare in ![]() din interiorul
intervalului I. Deci exista
din interiorul
intervalului I. Deci exista ![]() astfel incat
astfel incat ![]() De aici
De aici![]() Punem
Punem ![]() si inmultim
prima egalitate cu
si inmultim
prima egalitate cu ![]() si a doua cu t
si le adunam, cand avem:
si a doua cu t
si le adunam, cand avem: ![]() relatie ce contrazice convexitatea lui f.
relatie ce contrazice convexitatea lui f.
2. Sa se arate
ca intr-un triunghi ABC avem: ![]() .
.
R. Functia ![]() este concava. Conform
inegalitatii lui Jensen
este concava. Conform
inegalitatii lui Jensen 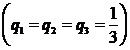
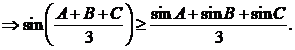 Cum
Cum ![]() inegalitatea se
rescrie:
inegalitatea se
rescrie: ![]() .
.
Functii injective, surjective, bijective
Definitia functiei injective. Proprietati
Fie o functie ![]() .
.
Definitie: Functia f se numeste injectiva (sau inca injectie)
daca: 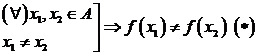
Asadar o functie f este injectiva daca la
argumente diferite ![]() le corespund prin f
imagini diferite
le corespund prin f
imagini diferite ![]()
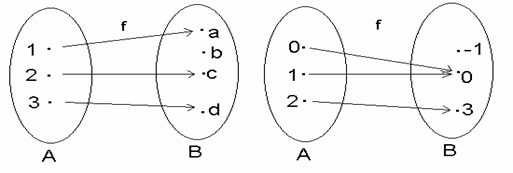
Functia f este injectiva Functia f nu este injectiva
Analizand functiile prezentate mai sus prin "diagrame" constatam ca o functie f este injectiva daca la elementele codomeniului ajunge celmult o "sageata". Functia f nu este injectiva daca cel putin la un element al codomeniului ajung cel putin doua "sageti".
De obicei pentru a proba ca o functie este injectiva se
utilizeaza negatia reciprocei implicatiei ![]() .
.
Mai precis are loc urmatoarea:
Propozitie: Functia ![]() este injectiva daca
este injectiva daca 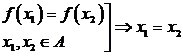 .
.
Demonstratia propozitiei este imediata.
Pentru a proba ca o functie
nu este injectiva se gasesc doua elemente ![]() astfel incat
astfel incat ![]() .
.
De exemplu, functia ![]()
![]() nu este injectiva
deoarece exista
nu este injectiva
deoarece exista ![]() pentru care
pentru care![]()
Monotonie si injectivitate
Are loc urmatoarea:
Propozitie: Orice functie strict monotona este injectiva.
Demonstratie: Fie ![]() strict
crescatoare (analog se procedeaza daca este strict
descrescatoare). Sa aratam ca f este injectiva
adica daca
strict
crescatoare (analog se procedeaza daca este strict
descrescatoare). Sa aratam ca f este injectiva
adica daca ![]()
Din ![]() sau
sau ![]() . Daca
. Daca ![]() , atunci
, atunci ![]() , adica
, adica ![]() .
.
La fel din ![]() rezulta
rezulta ![]() , adica
, adica ![]()
Operatia de compunere si functiile injective
Daca ![]() sunt doua
functii injective. Ce se poate spune despre functia
sunt doua
functii injective. Ce se poate spune despre functia ![]() Este oare de asemenea injectiva?
Raspunsul este afirmativ dat de urmatoarea:
Este oare de asemenea injectiva?
Raspunsul este afirmativ dat de urmatoarea:
Propozitie: Daca ![]() sunt functii injective atunci
sunt functii injective atunci ![]() este o functie
injectiva. (Compunerea a doua functii injective este tot o
functie injectiva).
este o functie
injectiva. (Compunerea a doua functii injective este tot o
functie injectiva).
Demonstratie: Trebuie
aratat ca daca ![]() , atunci
, atunci ![]() . Din
. Din ![]() Cum g este
injectiva de aici rezulta
Cum g este
injectiva de aici rezulta ![]() . In fine, cum si f este injectiva deducem ca
. In fine, cum si f este injectiva deducem ca ![]() .
.
Observatie: Aratati
ca daca ![]() este injectiva, atunci f este
injectiva.
este injectiva, atunci f este
injectiva.
Exemple studiate de functii injective
1) Functia de gradul intai
![]() este injectiva.
este injectiva.
Intr-adevar aratam ca daca ![]() , atunci
, atunci ![]() Din
Din ![]() rezulta
rezulta ![]() sau
sau ![]() . Cum
. Cum ![]() de aici rezulta
de aici rezulta ![]()
Observatie: Functia de gradul intai fiind strict monotona este injectiva.
2) Functia cubica ![]() este injectiva.
este injectiva.
Fie ![]() . De aici
. De aici ![]() . Produsul este zero daca cel putin unul din
factori este zero. Deci
. Produsul este zero daca cel putin unul din
factori este zero. Deci ![]() , adica
, adica ![]() sau
sau ![]() Ultima egalitate este imposibila deoarece gandita
ca o ecuatie de gradul al doilea in
Ultima egalitate este imposibila deoarece gandita
ca o ecuatie de gradul al doilea in ![]() (sau
(sau![]() ) aceasta nu are radacini reale pentru ca
discriminantul ei este negativ. Ramane deci
) aceasta nu are radacini reale pentru ca
discriminantul ei este negativ. Ramane deci ![]() . Daca
. Daca ![]() , atunci
, atunci ![]() .
.
Prin urmare daca ![]() se obtine
se obtine ![]() , ceea ce arata ca f este injectiva.
, ceea ce arata ca f este injectiva.
Observatie: Functia cubica fiind strict crescatoare este injectiva.
3) Functia radical de
ordin 2, ![]() este injectiva,
deoarece din
este injectiva,
deoarece din ![]() rezulta
rezulta ![]() sau
sau![]() .
.
Analog ![]() este injectiva.
este injectiva.
Observatii: Aceasta functie fiind strict crescatoarea este injectiva.
4) Functia radical de
ordin 3, ![]() este injectiva.
In general
este injectiva.
In general ![]() este injectiva.
este injectiva.
Observatii: Aceasta functie fiind strict crescatoare este injectiva.
Daca functiei f i se cunoaste graficul, atunci se poate preciza daca functia f este sau nu injectiva.
Pentru a stabili rezultatul se impun cateva precizari.
Daca ![]() este o functie
numerica
este o functie
numerica ![]() , atunci in trasarea graficului in reperul cartezian
, atunci in trasarea graficului in reperul cartezian ![]() se pun in
evidenta puncte
se pun in
evidenta puncte ![]() unde
unde ![]() .
.
Grafic
Multimii A ii corespund puncte de pe axa ![]() iar multimii B puncte de pe axa
iar multimii B puncte de pe axa ![]() (vezi figura). Am
marcat mai ingrosat aceste multimi pe fiecare axa.
(vezi figura). Am
marcat mai ingrosat aceste multimi pe fiecare axa.
Este clar ca ![]()
Daca functia este injectiva, atunci la un element ![]() ajunge prin f cel mult
un element
ajunge prin f cel mult
un element ![]() , adica
, adica ![]() . Sa retinem si aceasta ultima
formulare care ofera un alt mod de a stabili daca o functie este
injectiva.
. Sa retinem si aceasta ultima
formulare care ofera un alt mod de a stabili daca o functie este
injectiva.
Dar ![]() reprezinta
ecuatia unei drepte paralele cu axa
reprezinta
ecuatia unei drepte paralele cu axa ![]() . Pentru a vedea daca exista
. Pentru a vedea daca exista ![]() astfel incat
astfel incat ![]() , dreapta
, dreapta ![]() ar trebui sa
intersecteze graficul functiei. Acest punct (sau puncte) de
intersectie are abscisa (abscisele)
ar trebui sa
intersecteze graficul functiei. Acest punct (sau puncte) de
intersectie are abscisa (abscisele) ![]() pentru care
pentru care ![]() .
.
Acum este usor de stabilit urmatoarea:
Regula: Functia ![]() este injectiva daca orice paralela
este injectiva daca orice paralela ![]() dusa printr-un
punct al codomeniului la axa
dusa printr-un
punct al codomeniului la axa ![]() intersecteaza
graficul in cel mult un punct.
intersecteaza
graficul in cel mult un punct.
Functia f nu este
injectiva, daca exista cel putin o paralela
dusa printr-un punct al codomeniului la axa ![]() care intersecteaza graficul in cel putin doua
puncte.
care intersecteaza graficul in cel putin doua
puncte.
Grafic
Al treilea mod de abordare al injectivitatii unei
functii utilizeaza o idee pe care am prezentat-o mai sus:
functia f este injectiva daca la un elemnt ![]() , ajunge prin f cel mult un element
, ajunge prin f cel mult un element ![]() , adica
, adica ![]() are cel mult o
solutie.
are cel mult o
solutie.
Revenim asupra exemplelor analizate.
1) Functia de gradul intai: ![]() este injectiva
deoarece pentru
este injectiva
deoarece pentru ![]() , arbitrar ales ecuatia
, arbitrar ales ecuatia ![]() (are cel mult o
solutie). Intr-adevar
(are cel mult o
solutie). Intr-adevar ![]() reprezinta
solutia unica a ecuatiei.
reprezinta
solutia unica a ecuatiei.
2) Functia cubica ![]() este
injectiva pentru ca ecuatia
este
injectiva pentru ca ecuatia ![]() arbitrar (fixat) are cel mult o solutie (chiar o
solutie). Din
arbitrar (fixat) are cel mult o solutie (chiar o
solutie). Din ![]() rezulta
rezulta ![]() , cu unica solutie reala
, cu unica solutie reala ![]()
3) Functia radical de ordin 2, ![]() este injectiva
deoarece pentru orice
este injectiva
deoarece pentru orice ![]() ecuatia
ecuatia ![]() are cel mult o
solutie
are cel mult o
solutie ![]() Avem
Avem ![]()
4) Functia radical de ordin 3, ![]() este injectiva
pentru ca ecuatia
este injectiva
pentru ca ecuatia ![]() , arbitrar fixat are cel mult o solutie
, arbitrar fixat are cel mult o solutie ![]() . Intr-adevar din
. Intr-adevar din ![]()
Exemple de functii care nu sunt injective
1) ![]() Pentru
Pentru ![]() arbitrar fixat,
ecuatia
arbitrar fixat,
ecuatia ![]() are mai mult de o
solutie. Intr-adevar din
are mai mult de o
solutie. Intr-adevar din ![]()
2) ![]() Pentru
Pentru ![]() , ecuatia
, ecuatia ![]() .
.
3) ![]() Pentru
Pentru ![]() ecuatia
ecuatia ![]() are cel putin
solutiile
are cel putin
solutiile ![]()
4) ![]() Pentru
Pentru ![]() ecuatia
ecuatia ![]() are cel putin
solutiile
are cel putin
solutiile ![]()
Observatie: Daca 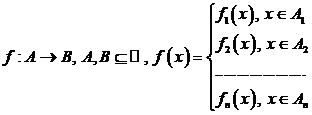
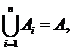
![]() si
si ![]() ,
, ![]() atunci faptul ca
f este injectiva se poate proba aratand ca
atunci faptul ca
f este injectiva se poate proba aratand ca ![]() Multimile
Multimile ![]() sunt situate pe axa
sunt situate pe axa ![]()
Definitia functiei surjective. Proprietati
Fie o functie ![]() .
.
Definitie: Functia f
se numeste surjectiva (sau
inca surjectie) daca
pentru orice ![]() exista cel putin un element
exista cel putin un element ![]() astfel incat
astfel incat ![]()
Cu alte cuvinte functia f este surjectiva daca orice
element (y) al codomeniului (B) este imaginea prin f a cel putin unui
element (x) din domeniul (A) al functiei. Functia f nu este surjectiva daca
exista cel putin un element y al codomeniului astfel incat ![]() sa rezulte
sa rezulte ![]()
Iata doua functii definite prin "diagrame".
Grafic
Daca functia f este definita printr-o diagrama, atunci f este surjectiva daca la fiecare element al codomeniului ajunge cel putin o "sageata".
Functia f nu este surjectiva daca exista cel putin un element al codomeniului la care nu ajunge nici o "sageata".
Observatie
importanta: Elementul ![]() care apare in
definitie se obtine rezolvand ecuatia
care apare in
definitie se obtine rezolvand ecuatia ![]()
Tehnicile de lucru prin care am probat ca f este injectiva se aplica si pentru o functie surjectiva cu anumite corectii impuse de definitia functiei surjective. Mai precis are loc urmatoarea:
Regula: Functia ![]() este surjectiva daca orice
paralela
este surjectiva daca orice
paralela ![]() dusa printr-un
punct al codomeniului la axa
dusa printr-un
punct al codomeniului la axa ![]() intersecteaza
graficul in cel putin un punct.
intersecteaza
graficul in cel putin un punct.
Functia f nu este surjectiva daca
exista cel putin o paralela dusa printr-un punct al
codomeniului la axa ![]() care nu
intersecteaza graficul in nici un punct.
care nu
intersecteaza graficul in nici un punct.
Dupa cum se poate constata, functiile analizate cu ajutorul graficelor la functiile injective sunt si surjective.
Functia ![]() nu este
surjectiva deoarece pentru
nu este
surjectiva deoarece pentru ![]() o paralela
dusa prin acest punct al codomeniului la
o paralela
dusa prin acest punct al codomeniului la ![]() nu taie graficul in
nici un punct.
nu taie graficul in
nici un punct.
Grafic
Dar functia ![]() este surjectiva.
este surjectiva.
Alt mod de a proba surjectivitatea functiei ![]() este de a arata
ca ecuatia in x,
este de a arata
ca ecuatia in x, ![]() are cel putin o
solutie
are cel putin o
solutie ![]() .
.
Sa reluam exemplul de mai sus. Fie ![]()
Pentru ![]() ecuatia
ecuatia ![]() adica
adica ![]() evident nu are
solutie. Deci f nu este surjectiva.
evident nu are
solutie. Deci f nu este surjectiva.
Observatie: Daca 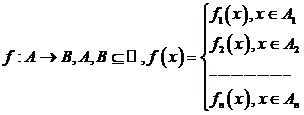 ,
, 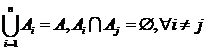 si
si ![]() , atunci faptul ca f este surjectiva se poate proba
aratand ca
, atunci faptul ca f este surjectiva se poate proba
aratand ca 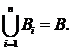 Multimile
Multimile ![]() sunt situate pe axa
sunt situate pe axa ![]()
Compunere si surjectivitate
Legat de compunerea a doua functii surjective are loc urmatoarea:
Propozitie. Daca ![]() sunt doua functii surjective, atunci si
functia
sunt doua functii surjective, atunci si
functia ![]() este surjectiva.
este surjectiva.
Grafic
Demonstratie: Sa aratam ca pentru orice ![]() exista cel
putin un element
exista cel
putin un element ![]() astfel incat
astfel incat ![]() Fie deci
Fie deci ![]() Cum functia g
este surjectiva exista cel putin un element
Cum functia g
este surjectiva exista cel putin un element ![]() astfel incat
astfel incat ![]() .
.
Functia f fiind de asemenea surjectiva pentru ![]() (gasit mai sus)
exista
(gasit mai sus)
exista ![]() astfel incat
astfel incat 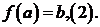
Din (1) si (2) rezulta ![]() sau
sau ![]() .
.
Observatie: Aratati
ca daca ![]() este surjectiva, atunci g este surjectiva.
este surjectiva, atunci g este surjectiva.
Definitia functiei bijective. Proprietati.
Fie o functie ![]() .
.
Definitie: Functia f se numeste bijectiva (sau inca bijectie) daca f este atat injectiva cat si surjectiva.
Tinand seama de cele spuse la functia injectiva cat si surjectiva, functia f este bijectiva daca orice element (y) al codomeniului (B) este imaginea prin f a unui singur element (x) din domeniul (A) al functiei.
Altfel spus:
Functia f este bijectiva daca pentru orice ![]() ecuatia
ecuatia ![]() are o unica
solutie in A.
are o unica
solutie in A.
Daca este dat graficul functiei f, atunci:
Regula: Functia ![]() este bijectiva daca orice
paralela
este bijectiva daca orice
paralela ![]() dusa printr-un
punct al codomeniului la axa
dusa printr-un
punct al codomeniului la axa![]() intersecteaza graficul in exact un punct.
intersecteaza graficul in exact un punct.
O functie bijectiva se mai numeste si corespondenta "one to one", adica o corespondenta "unu la unu".
Daca functia este data printr-o diagrama, atunci ea este bijectiva daca la orice element din codomeniu soseste o singura sageata.
Grafic
Functia f este bijectiva.
Exemple studiate de functii bijective
1)
Functia de
gradul intai ![]() este bijectiva
deoarece este atat injectiva cat si surjectiva.
este bijectiva
deoarece este atat injectiva cat si surjectiva.
2)
Functia
cubica ![]() fiind atat
injectiva cat si surjectiva este bijectiva.
fiind atat
injectiva cat si surjectiva este bijectiva.
3)
Functia
radical de ordin 2 ![]() este bijectiva fiind
injectiva si surjectiva
este bijectiva fiind
injectiva si surjectiva
4)
Functia
radical de ordin 3 ![]() este bijectiva
deoarece este injectiva si surjectiva
este bijectiva
deoarece este injectiva si surjectiva
5)
Functia
sinus restrictionata la 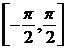 pe care o
notam tot
pe care o
notam tot 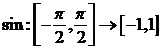 este bijectiva,
avand graficul redat mai jos. Se constata ca orice dreapta
este bijectiva,
avand graficul redat mai jos. Se constata ca orice dreapta ![]() taie graficul in exact
un punct.
taie graficul in exact
un punct.
Grafic
6)
Functia
cosinus restrictionata la ![]() si
notata tot
si
notata tot ![]() este de asemenea bijectiva.
este de asemenea bijectiva.
Grafic
7)
Functia
tangenta restrictionata la 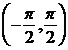 si
notata tot
si
notata tot 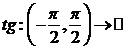 este bijectiva.
este bijectiva.
Grafic
8)
Functia
cotangenta restrictionata la ![]() si
notata tot
si
notata tot ![]() este bijectiva
este bijectiva
Grafic
Compunere si bijectivitate
Tinand seama de comportarea functiilor injective si surjective in raport cu operatia de compunere se stabileste usor urmatoarea:
Propozitie: Daca ![]() sunt doua
functii bijective, atunci functia
sunt doua
functii bijective, atunci functia ![]() este bijectiva.
este bijectiva.
Conditia necesara si suficienta ca o functie sa fie inversabila
Daca A este o multime, atunci
functia ![]() se numeste
functia identica a multimii A.
se numeste
functia identica a multimii A.
Reamintim definitia pentru o functie inversabila.
Definitie:
O
functie ![]() se numeste inversabila
se numeste inversabila