Camp de evenimente. camp de probabilitate. scheme probabilistice clasice

CAMP DE EVENIMENTE. CAMP DE PROBABILITATE. SCHEME PROBABILISTICE CLASICE

&1.Evenimente. Categorii de evenimente

Lucrurile, fiintele sau fenomenele care printr-o proprietate comuna pot fi considerate impreuna constituie o multime, o colectivitate, o populatie. Fiintele sau fenomenele care constituie o colectivitate sunt numite elementele colectivitatii.

Fie data o colectivitate (populatie) E, cu elementul generic e. Elementele colectivitatii E poseda sa nu poseda anumite proprietati rezultate din studiul ei. Proprietatea considerata constituie criteriul de cercetare a multimii respective. Realizarea practica a complexului de conditii corespunzatoare criteriului de cercetare este numita experienta. Aplicarea experientei asupra unui element al populatiei este numita proba. Rezultatul unui experiment (realizarea unui anumit criteriu in urma unei probe) este numit eveniment (in teoria probabilitatilor, notiunea de eveniment este o notiune primara). Este evident, ca un eveniment poate sau nu poate avea loc.

Fie o anumita experienta care ne poate da un anumit rezultat A_i dintr-o multime finita de rezultate posibile ,i=1,2,,n;evenimentul A_i care poate fi realizat de o proba si numai de una, se numeste eveniment elementar. Restul evenimentelor se numesc evenimente compuse.

Vorbind de o colectivitate E, totdeuna suntem pusi in fata criteriului de cercetare care a permis constituirea colectivitatii respective, numit criteriul fundamental, care determina relatia de apartenenta e I E. Corespunzator acestui criteriu fundamental se ataseaza evenimentul sigur, E, deoarece in experienta respectiva (constituirea colectivitatii), proba realizeaza totdeuna criteriul de apartenenta.

Fie dat evenimentul sigur E corespunzator multimii E, ale carei elemente sunt supuse unor criterii de cercetare care duc la considerarea unor evenimenete . Sa notam cu X un anumit eveniment sicu X multimea elementelor e din E care satisfac acestui eveniment. In acest mod este realizata urmatoarea dubla corespondenta biunivoca (intre elemente si multimi corespunzatoare): E E , X X.

Deoarece intre multimile E si X exista relatia de incluziune, X E, definim o relatie analoaga pentru evenimentele X si E, numita relatia de implicatie, pe care o scriem: X E, citind, 'evenimentul X este implicat in evenimentul sigur E'.

Aceasta relatie de implicatie, poate prezenta urmatoarele situatii:

1) X=E sau X=I, cand toate elementele e din E satisfac criteriul care determina evenimentul X; in acest caz X=E, adica in orice proba are loc evenimentul X. Numim acest eveniment X eveniment cert (sigur);

2) X E, cand unele elemente e din E satisfac criteriul care determina evenimentul X, altele nu; in aces caz, notam X E, ceea inseamna ca in unele probe are loc evenimentul X, in altele nu.Numim in acest caz evenimentul X eveniment intamplator sau eveniment aleator sau inca eveniment stocastic.

3) X=F, cand nici un element e din E nu satisface criteriul care determina evenimentulX; in acest caz, vom nota X=F, ceea ce inseamna ca in nici o proba nu are loc evenimentul X. Numim acest eveniment X eveniment imposibil.

Fie evenimentul sigur E, si evenimentul A. Numim eveniment contrar al evenimentului A, evenimentul notat A (sau A^C,sau inca CA), care consta in nerealizarea evenimentului considerat A (A este evenimentul care se produce ori de cate ori nu se produce A).

In particular, E = F F = E.

Dat fiind corespondenta biunivoca dintre multime si eveniment, in continuare nu vom face distinctie in notatie, intre multime si eveniment.

Problema compararii evenimentelor X,Y intre ele are sens atata timp cat X E si Y E.Distingem:

1) Evenimentul X implica evenimentul Y, (X Y) sau evenimentul Y este implicat de evenimentul X, daca evenimentul Y se realizeaza de fiecare data cand se realizeaza evenimentul X (multimile corespunzatoare sunt in aceeiasi relatie de incluziune). In particular: F X E.

2) Doua evenimente se numesc echivalente (evenimente echialeatoare), (X = Y),daca evenimentul X implica evenimentul Y si in acelasi timp evenimentul Y implica evenimentul X (multimile corespunzatoare sunt egale).

Proprietati ale relatiei de implicatie intre evenimente:

a) A B si B C T A C, tranzitivitatea relatiei

b) A B si B A A=B, antisimetria relatiei

c) a A, reflexivitatea relatiei

d) Nu pentru orice A,B avem: A B sau B A.

Fiind date mai multe evenimente, realizarea lor ne conduce a le privi sub diverse aspecte: realizarea sau nerealizarea lor impreuna, realizarea unora este conditionata sau nu de realizarea celorlalte evenimente. In functie de aceste consideratii, distingem urmatoarele categorii de evenimente:

1) Doua sau mai multe evenimente se numesc incompatibile daca producerea unuia dintre ele, exclude posibilitatea producerii celorlalte in aceeasi proba; in caz contrar, cand se pot realiza simultan sunt numite evenimente compatibile.

2) Doua evenimente se numesc independente, daca realizarea unuia nu influenteaza realizarea celuilalt; in caz contrar, cand realizarea unui eveniment influenteaza realizarea altui eveniment, ele sunt numite evenimente dependente.

3) Daca A si B sunt doua evenimente dependente si daca realizarea evenimentului B este conditionata de realizarea evenimentului A, atunci vom nota B/A intelegand ca 'evenimentul B are loc numai daca are loc evenimentul A' si vom citi 'B conditionat de A'.

Observatie.

Problema compatibilitatii sau a incompatibilitatii a doua evenimente A si B este pusa, presupunand indeplinita relatia de implicatie a acestor evenimente fata de un acelasi eveniment sigur E.

Problema dependentei evenimentelor A si B necesita implicatia lor fata de un acelasi eveniment eveniment sigur,pe cand problema independentei nu necesita implicatia fata de un acelasi eveniment sigur.

&2. Operatii cu evenimente

Pornind de la analogia dintre multime si eveniment, operatiile intre multimi permit definirea unor operatii analoage intre evenimente.

1) Fie A si B doua evenimente. Notam S = A B si vom numi evenimentul S suma sau reuniunea lor, evenimentul care se produce daca se produce evenimentul A, sau evenimentul B, sau se produc ambele evenimente A si B (evenimentul A B se mai citeste 'A sau B' ).

In cazul unui sistem de n evenimente: A_i,i=1,2,,n atunci vom nota reuniunea lor prin

A₁ A₂ A_n = ,

si este evenimentul care se realizeaza atunci cand se realizeaza cel putin unul din ele.

Observatie. Daca sunt toate rezultatele posibile ale unei experiente, atunci:

E = A₁ A₂ A_n .

2) Fiind date doua evenimente A si B, vom numi produsul sau intersectia lor, evenimentul notat A B, care se produce daca se produce atat evenimentul A cat si evenimentul B (evenimentul A B se mai citeste 'A si B' ).

In cazul unui sistem de n evenimente: A_i ,i=1,,n intersectia lor se scrie :

A₁ A₂ A_n =

si acest eveniment se realizeaza atunci cand se realizeaza simultan evenimentele A₁,,A_n.

Observatii.

a) Doua evenimente A si B sunt disjuncte daca A B=F. Aceasta proprietate este caracteristica evenimentelor

incompatibile.

b) Operatia de reuniune a evenimentelor are sens pentru evenimente incompatibile si compatibile; operatia de intersectie a evenimentelor are sens pentru evenimente independente si dependente.

c) A = E si A = F

3) Diferenta evenimentelor A si B, este evenimentul notat A-B, care se produce atunci si numai atunci, cand se produce evenimentul A, dar nu se produce evenimentul B.

Din definitie,deducem:

a) A - B = A ;

b) , (inductiv)

deci orice reuniune de evenimente se poate scrie ca o reuniune de evenimente incompatibile.

Operatiile cu evenimente, analoage operatiilor cu multimi, au urmatoarele proprietati care se verifica folosind definitiile date:

1. comutativitatea: A B=B A,

A B=B A;

2. asociativitatea: (A B) C=A (B C),

(A B) C=A (B C);

3.Operatiile si intre ele sunt distributive:

A (B C)=(A B) (A C);

A (B C)=(A B) (A C);

4. A E=A , A E =E;

5. A F=A , A F F

6. daca A B, atunci: A B=B, A B=A;

7. daca A C, B C, atunci: A B C, A B C;

8. A A=A, A A=A;

9. absorbtie: (A B) B=B, A (A B)=A.

&3. Camp de evenimente

Multimea tuturor evenimentelor legate de o experienta inclusiv evenimentul sigur si evenimentul imposibil,formeaza un camp de evenimente.

Daca de exemplu,E= ,reprezinta multimea evenimentelor elementare generate de o experienta oarecare, atunci evenimentele care constituie campul de evenimente sunt:

F .. in numar de

A₁,A₂, , A_n .. in numar de   

A_i A_j , (i j) in numar de

A_i A_j A_k , (i j k) . in numar de

A₁ A₂ A_n=E . in numar de .

In total: evenimente care compun campul de evenimente.

Daca E= , evenimentul sigur cu A_i, i=l,,n multimea tuturor evenimentelor posibile legate de o anumita experienta, atunci campul de evenimente corespunzator va fi notat E,K , unde K = P(E), multimea tuturor partilor multimii E.

Observatie. Un camp de evenimente este o multime partial ordonata. Un camp de evenimente este finit daca multimea E este o multime finita. In caz contrar, campul de evenimente este infinit.

Prin definitie, evenimentele A₁,A₂,,A_n formeaza un sistem complet de evenimente daca un experiment conduce la unul si numai unul dintre aceste evenimente, adica:

1.A_i A_j= F, (i j);

2.A₁ A₂ A_n = E.

Observatie. Evenimentele A si ; E si F formeaza un sistem complet de evenimente.

Fie dat intr-un camp de evenimente E,K un sistem de evenimente: si un eveniment A I E,K astfel incat:

1.A_i A_j = F , i j ; i,j = 1,2,,m;

2.A = A₁ A₂ A_m .

In acest caz se spune ca sistemul de evenimente dat reprezinta o desfacere sau partitie a evenimentului A.

In particular,considerand evenimentul sigur EI E,K , atunci un sistem complet de evenimente: determina o partitie sau o desfacere a evenimentului sigur.

Observatie. Din XI E,K si X E,deducem ca orice eveniment X al campului de evenimente, poate fi scris ca o reuniune de evenimente elementare, adica:

X = A₁ A₂ A_k , k n.

&4. Axiomele campului de evenimente

Un camp de evenimente poate fi caracterizat ca fiind o multime de evenimente ce satisface urmatoarele proprietati, numite axiomele campului de evenimente E,K

A₁. daca X E, atunci evenimentele X,I E,K

A₂. daca X,YI E,K , atunci X YI E,K

Consecinte.

1) Evenimentul sigur EI E,K

In adevar, daca XI E,K , atunci I E,K (ax.A₁) si X =EI E,K , (ax.A₂).

2) Evenimentul imposibil FI E,K

In adevar, din EI E,K obtinem =FI E,K

3) Daca A_iI E,K , i=1,2,,p atunci si evenimentul

B_p = (A₁ A₂ A_p)I E,K

Justificarea se face folosind inductia matematica.

Pentru doua evenimente, proprietatea este adevarata (ax.A₂). In ipoteza, ca proprietatea este adevarata pentru p-1 evenimente, adica evenimenteul B_p-1I E,K , atunci evenimentul B_p = B_p-1 A_pI E,K , (ax.A₂, pentru B_p-1 si A_p).

4) Oricare ar fi evenimentele X,Y din E,K , avem ca evenimentul X YI E,K

In adevar, din X,YI E,K T I E,K T I E,K T = X YI E,K

5) In multimea de evenimente ale campului de evenimente E,K , exista o submultime , numita multimea evenimentelor elementare, cu proprietatile:

a) A_i F , i=1,2,,n;

b) A_i A_j = F, i j ; i,j=1,2,,n;

c) A₁ A₂ A_n = E;

d) in campul de evenimente E,K exista cel putin un eveniment oarecare A care nu este elementar, (A A_i , i= 1, 2,,n) in asa fel ca pentru cel putin un i avem A_i A. De aici, rezulta ca oricare eveniment al campului este o reuniune de evenimente elementare. In particular, proprietatea este adevarata si pentru evenimentul sigur E.

6) Pentru doua evenimente A ,BI E,K , are loc una din: A B, A = B, A B.

Prin definitie, o multime nevida B are o structura de algebra Boole, daca s-au definit doua operatii algebrice binare (reuniunea si intersectia) si o operatie algebrica unara (complementarierea) peste tot definite pe B, satisfacand axiomele:

B₁: comutativitatea reuniunii si intersectiei;

B₂: asociativitatea reuniunii si intersectiei;

B₃. absorbtie;

B_4. distributivitatea reuniunii fata de intersectie si invers;

B₅. complementarietate.

7)Campul de evenimente are o structura de algebra Boole.

&5. Marimi si masura lor

O anumita proprietate care are diferite forme de prezentare, notate A,B,C, este considerata marime daca in multimea formelor de existenta a acestei proprietati sunt satisfacute urmatoarele proprietati, numite axiome ale marimii:

A₁. Ax. identitatii. Intotdeuna are loc A = A;

A₂. Ax. reflexivitatii. Relatia A=B este tot una cu B=A;

A₃. Ax.compararii. Intre elementele multimii proprietatii considerate exista o relatie de ordine pe care o notam simbolic cu ' < ' sau ' > ', iar intre doua elemente oarecare A si B exista una din relatiile:

A < B , A = B , A > B ;

A₄. Ax.tranzitivitatii. Pentru oricare din semnele ' < , = , > ' s ' , avem: A B si B C T A C;

A₅. Proprietatea considerata este omogena si aditiva, adica exista A,B,C astfel ca: A + B = B + A = C.

Masura unei marimi este o functie de proprietatea care constituie marimea respectiva, care la randul ei satisface anumitor proprietati pe care le numim, axiomele masurii:

Fie X marimea considerata si m(X) functia masura.

A₁. m(X) 0 ,oricare ar fi X;

A₂. m(F) = 0 ;

A₃. masura este aditiva, adica daca:

, X_i X_j =F , i j ; i,j=1,2,,n avem:

m(X) =

Observatie. Functia masura m(X) se alege de obicei prin raportarea masurii la o masura etalon.

&6. Masura realizarii evenimentelor. Probabilitate.

Definitia clasica a probabilitatii. Frecvente

Fie dat un camp de evenimente E,K

Numim probabilitatea unui eveniment X o functie de eveniment care masoara realizarea lui, pe care o notam P(X).

Evenimentul etalon, va fi luat evenimentul sigur E, considerand P(E) = 1.

Probabilitatea P(X) a unui eveniment XI E,K este o functie care, conform proprietatilor generale ale masurii, indeplineste urmatoarele conditii, numite axiomele probabilitatii si anume :

P₁. daca XI E,K , atunci P(X) 0 ;

P₂. P(E) = 1 ;

P₃. daca X,YI E,K , X Y = F , atunci

P(X Y) = P(X) + P(Y).

Consecinte.

1. P(X) + P() = 1, (X =E , X =F

2. P()=1-P(X). In particular, P(F)=1-P(E)=0;

3. daca XI E,K T 0 P(X) 1;

4. Daca X₁,X₂,,X_n este un sistem de evenimente, astfel incat: X_kI E,K , k=1,2,,n; X _i X_j = F, i j ;i,j=1,,n atunci:

P(B_n) = P(

In adevar,proprietatea fiind adevarata pentru n=2 (ax.P₃), in ipoteza ca este adevarata si pentru n-1,avem:

P(B_n)=P(B_n-1 X_n)=P(B_n-1)+P(X_n) T

P(B_n)=

Fie dat in campul E,K un sistem de evenimente elementare: , E_kI E,K , k=1,2,,n ; E_i E_j = F, i j, i,j=1,2,,n care reprezinta o desfacere a evenimentului sigur E.

Deoarece realizarea oricarui eveniment elementar E_k, k=1,2,,n duce la realizarea evenimentului sigur E, evenimentele E_k , k=1,,n mai sunt numite evenimente posibile sau cazuri posibile. Admitem ca toate evenimentele posibile E_k sunt echiprobabile (egal posibile sau au aceeasi sansa de a se realiza), adica avem: P(E_k)=p ,k=1,2,,n .

Din relatia

P( adica probabilitatea realizarii unui eveniment elementar, cand toate evenimentele elementare sunt egal posibile, este 1/n (n reprezinta numarul evenimentelor posibile).

Fie un eveniment oarecare X I E,K

In acest caz, evenimentul X poate fi exprimat printr-o desfacere de x evenimente alementare E_k, x n , adica avem:

X = , (sau X =

unde prin F s-a notat x indici din cei n indici ai evenimentelor elementare prin realizarea carora se realizeaza evenimentul X.

Deoarece:

P(X) = P(P(X)=x.p

(deoarece sunt x termeni). Apoi,p=1/n, de unde P(X)=x/n.

Acest rezultat, cunoscut sub denumirea de definitia clasica a probabilitatii, poate fi formulata astfel:

Probabilitatea realizarii unui eveniment X este data de raportul dintre numarul cazurilor favorabile realizarii evenimentului X si numarul cazurilor posibile,toate cazurile fiind considerate egal posibile.

Observatie. Functia P(X)=x/n, implica indeplinirea conditiilor: n numarul cazurilor posibile si x numarul cazurilor favorabile sa fie finite.

Tinand cont ca la acest rezultat s-a ajuns respectand axiomele probabilitatii, trebuie atunci scos in evidenta alt sens al numerelor n si x, decat acela dat prin particularizarea facuta cand am fost condusi la definitia clasica a probabilitatii.

Mai general, daca: m(E), masura multimii care corespunde evenimentului sigur E si m(X), masura multimii care corespunde evenimentului X E, atunci:

P(X) =

rezultat care constituie expresia generala a probabilitatii :

Probabilitatea realizarii unui eveniment X E este data de raportul dintre masura multimii ce realizeaza evenimentul considerat X si masura multimii ce realizeaza evenimentul sigur E.

Observatii.

1) Definitia clasica devine un caz particular al acesteia, luand m(X) = x , m(E) = n .

2) Expresia generala a functiei de probabilitate da posibilitatea sa se inlature greutatile care survin in cazul colectivitatilor infinite, atat cele discrete cat si cele continue, bineinteles cu precautia de a determina masura multimilor cu care lucram. De exemplu, daca marimile sunt continue si au imagini geometrice, ca segmente de dreapta, figuri plane sau corpuri, atunci se va lua ca masura lungimea, aria sau volumul multimii respective.

In cazul cand ne indreptam atentia spre studiul unui eveniment, numarand de cate ori s-a realizat acest eveniment, in probele efectuate, obisnuim a spune ca exprimam frecventa

absoluta a evenimentului respectiv.

Astfel frecventa absoluta atasata unui eveniment X E este acelasi lucru cu masura multimii discrete si finite corespunzatoare evenimentului X.

Considerand frecventele absolute ale evenimentelor X si E, se numeste frecventa relativa a evenimentului X E, notata cu f, raportul frecventelor absolute corespunzatoare, adica f=x/n .

Importanta notiunii de frecventa relativa se pune in evidenta atunci cand colectivitatea studiata nu este cunoscuta in totalitatea ei si suntem nevoiti a face cercetari partiale studiind subcolectivitati pentru care determinam frecventele relative ale evenimentului studiat.

&7. Probabilitati conditionate

Prin definitie, probabilitatea conditionata a evenimentului B de catre evenimentul A, notata P(B/A)=P_A(B), este probabilitatea evenimentului B in ipoteza ca evenimentul A s-a produs si

P_A(B) = .

Justificarea o vom face folosind definitia clasica a probabilitatii. Daca vom nota: cu n, numarul cazurilor posibile ale experimentului in urma caruia se pot produce evenimentele A si B; cu m, numarul cazurilor favorabile producerii evenimentului A, (m n); si cu m', numarul cazurilor favorabile producerii evenimentului B/A, (m' m), atunci:

Folosind si P_B(A),vom obtine:

,

adica probabilitatea producerii simultane a doua evenimente dependente este egala cu produsul dintre probabilitatea unuia dintre evenimente si probabilitatea conditionata a celuilalt eveniment, calculata in ipoteza ca primul eveniment a avut loc.

Observatii.

1) Calculul probabilitatii conditionate a unui eveniment, se face in ipoteza ca: A,B F

2) Daca avem n evenimente dependente A₁ ,,A_n atunci, folosind metoda inductiei matematice, obtinem:

P(B_n)=P(A₁)..

Relatia fiind adevarata pentru n=2,in ipoteza ca ea este adevarata pentru n-1,avem:

P(B_n) = P(B_n-1 A_n) = P(B_n-1)

=

&8. Probabilitatea evenimentelor rezultate din               operatii cu evenimente

A.Probabilitatea evenimentului suma

Reamintim ca operatia de adunare a evenimentelor are sens, pentru evenimente incompatibile si evenimente compatibile. Distingem:

a)Termenii sumei sunt evenimente incompatibile

In acest caz problema este rezolvata de axioma (P₃) a prbabilitatii pentru n=2, si de consecinta 4 a axiomelor probabilitatii pentru n termeni:

, A_i A_j = F , i j; i,j=1,,n .

Ne propunem sa verificam acest rezultat (pentru n=2), folosind definitia clasica a probabilitatii sau expresia generala a probabilitatii.

a₁) Fie

P(A) = , P(B) = .

Daca tinem cont pe de o parte ca la fiecare caz favorabil al evenimentului A corespund n' cazuri favorabile ale evenimentului A B (dupa definitia a reuniunii a doua evenimente, este indiferent ce se intampla cu B) adica m'n' cazuri favorabile, iar pe de alta parte, la fiecare caz favorabil al evenimentului B corespunde n' cazuri favorabile ale evenimentului A B, adica m'n' cazuri favorabile, deducem ca sunt m'n'+m'n' cazuri favorabile producerii evenimentului A B (nu putem avea cazuri favorabile comune caci A, B sunt evenimente incompatibile).

Un rationament analog, ne conduce la n'n' cazuri posibile realizarii evenimentului A B. Deci:

P(A B)=, sau

a₂) Folosind expresia generala a probabilitatii, fie A si B doua evenimente: A E, B E, A B=F T

m(A B) = m(A) + m(B) si

adica

P(A B) = P(A) + P(B) .

b) Termenii sumei sunt evenimente compatibile

b₁) Fie A si B doua evenimente compatibile: A E, B E si A B F. Deoarece A B F T

m(A B) = m(A) + m(B) - m(A B) , de unde

, adica

P(A B) = P(A) + P(B) - P(A B), sau

b₂) Din relatiile:

A = (A - B) (A B) si (A - B) (A B) = F

deducem

P(A) = P(A - B) + P(A + B) ,

de unde

P(A - B) = P(A) - P(A B).

In cazul particular, cand B A T P(B) P(A), (deoarece P(A - B) 0).

Cu aceasta, verificand ca au loc:

A B=A (B-A B) si A (B-A B) = F

deducem

P(A B) = P(A) + P(B-A B) =P(A) + P(B) -P(A B) deoarece A B B .

Mai general:

b₃) Daca A_i, i=1,2,,n sunt evenimente compatibile, atunci:

+

+ ,

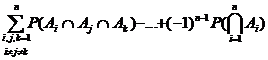(formula lui Poincaré).

Folosind metoda inductiei matematice, observam ca relatia este adevarata pentru n=2, din b₂). In ipoteza ca relatia este adevarata pentru n-1, obtinem:

= . Apoi,

- ,

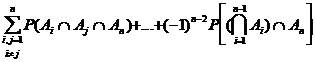care adaugata la relatia precedenta dupa care folosim ipoteza inductiva, ne va conduce la relatia ceruta.

Observatie. In particular, daca evenimentele A_k, k=1,,n sunt intre ele incompatibile: A_i A_j = F, A_i A_j A_k = F etc., atunci obtinem relatia cazului a) cand termenii sumei sunt evenimente incompatibile.

B. Probabilitatea evenimentului produs

Pentru evenimentul produs vom distinge situatiile dupa care evenimentele factori sunt evenimente independente, evenimente dependente sau evenimente oarecare (nu se stie daca sunt sau nu independente sau dependente).

a) Factorii produsului sunt evenimente independente

Fie A,B evenimente independente. Atunci

P(A B) = P(A).P(B),

adica probabilitatea producerii simultane a evenimentului A si B, este egala cu produsul probabilitatilor acestor evenimente.

In adevar,fie:

P(A) = m/n , P(B) = m'/n', (m n , m' n'), adica de exemplu n reprezinta numarul cazurilor incompatibile egal posibile ale experimentului in urma caruia poata sa se produca evenimentul A, etc.

Daca la fiecare din cele n cazuri egal posibile ale producerii evenimentului A, asociem cele n' cazuri posibile ale producerii evenimentului B, obtinem nn' cazuri posibile in care pot sa apara evenimentele: sau A si , sau A si B, sau si .

Numarul cazurilor favorabile este egal cu mm', deoarece la fiecare din cele m cazuri favorabile producerii evenimentului A, asociem m' cazuri favorabile producerii evenimentului B. Deci

P(A B) = .

Prin definitie, mai multe evenimente sunt independente in totalitatea lor, (mutual independente), atunci cand fiecare dintre ele si orice intersectie a lor (toate sau numai o parte), sunt evenimente independente.

Daca A_i , i=1,2,,n sunt evenimente independente in totalitatea lor, atunci:

=P(A₁).P(A₂) P(A_n) = .

Observatii.

1) Daca evenimentele A_i , i=1,,n sunt independente in totalitatea lor, atunci din formula lui Poincaré, obtinem:

+

+ =

= 1 - 1-P(A₁) 1-P(A₂) 1-P(A_n)

= .

2) La ultima forma a formulei precedente se poate ajunge si fara a face apel la formula lui Poincaré.

Fie evenimentele A_i, i=1,2,,n independente.

Evenimentul are loc cand are loc cel putin unul dintre evenimente, iar evenimentul , are loc daca au loc toate evenimentele , deci nu are loc nici un eveniment A_i. In acest caz, evenimentele si sunt evenimente contrarii, deci:

=

= 1 - ,

caci si sistemul evenimentelor contrarii , sunt evenimente independente.

3) Daca mai multe evenimente sunt independente doua cate doua, aceasta nu implica independenta in totalitatea lor.

b) Factorii produsului sunt evenimente dependente

Daca A si B sunt doua evenimente dependente, aceasta inseamna ca au loc evenimentele conditionate A/B sau B/A. In acest caz, vom folosi rezultatele gasite la probabilitatile conditionate.

c) Inegalitatea lui Boole

Fie evenimentele A_i, i=1,2,,n despre care nu cunoastem daca sunt independente sau dependente. In acest caz se poate demonstra o inegalitate, care da o limita inferioara a probabilitatii evenimentului produs:

In adevar, din relatia:

P(A B) = P(A) + P(B) - P(A B) si 0 P(A B) 0 deducem

P(A B) P(A) + P(B) -1 ,

adica inegalitatea data este adevarata pentru doua evenimente.

In ipoteza ca inegalitatea este adevarata pentru n-1 evenimente, obtinem:

Folosind ipoteza inductiva, avem:

Observatie. Pentru evenimentul suma (, se poate obtine o inegalitate care da valoarea maxima a evenimentului. Cand nu stim daca evenimentele sunt incompatibile sau nu, in ipoteza ca suma probabilitatilor evenimentelor este mai mica decat unitatea avem:

adica probabilitatea producerii a cel putin unui din evenimentele unui sistem , nu depaseste suma probabilitatilor acestor evenimente.

&9. Formula probabilitatii totale.Formula probabilitatii cauzelor (Bayes)

a) Fie A_i ,i=1,2,,n un sistem complet de evenimente.

Sa presupunem ca un eveniment oarecare XI E,K poate sa se produca conditionat de unul dintre evenimentele A_i, i=1,2,,n adica:

X=X E=(A₁ X) (A₂ X) (A_n X) .

Deoarece (A_i X) (A_j X)=F, i j; i,j=1,2,,n, adica evenimentele (A_i X ) si (A_j X), i j sunt incompatibile, vom putea scrie:

P(X)= ,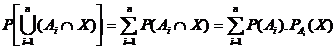

rezultat cunoscut sub numele de formula probabilitatii totale.

b) In aceleasi conditii ale sistemului de evenimente de la punctul a), fixandu-ne atentia asupra unui eveniment A_i , vom putea sa scriem:

P(A_i X)=P(A_i).,

de unde, obtinem o formula cunoscuta sub numele de formula probabilitatilor cauzelor sau formula lui Bayes (Th.Bayes -m.1763-, matematician englez. Paralel cu J.Bernoulli s-a ocupat de probabilitatea aposteriori, rezolvand pentru prima data aceasta problema fundamentala pentru aplicatii), care da probabilitatea evenimentului A_i in ipoteza ca evenimentul X s-a produs:

,

cu P(X) determinat la punctul a).

&10. Camp de probabilitate

Fie campul de evenimente E,K . Realizarea oricarui eveniment X E, deci X din E,K , este masurata de prbabilitatea P(X) (definita prin axiomele P₁-P₃, cunoscute de axiomele lui Kolmogorov). Deci, functia de eveniment P(X) are domeniul de definitie campul de evenimente E,K , iar drept multime a valorilor o multime pe care o numim camp de probabilitate, notat E,K;P

Observam ca pentru campul de probabilitate, functia P(X)I E,K;P indeplineste conditiile:

1. 0 P(X) 1, pentru orice X din E,K

2. P(X) P(Y), daca X Y cu x,yI E,K

Fiecare in parte, campul de evenimente E,K si campul de probabilitate E,K;P pot fi finite sau infinite. Dat fiind ca E,K;P este subordonat lui E,K , nu pot avea loc decat urmatoarele situatii:

&11. Scheme probabilistice clasice

Colectivitatile studiate in practica au caracteristici care duc la evenimente ce se realizeaza dupa scheme teoretice asemanatoare, grupandu-se in tipuri de scheme probabilistice. Intalnim:

a) Schema urnei cu bila nerevenita

Fie o urna in care sunt a bile albe si b bile negre. Din urna se extrag succesiv n bile, fara a pune bila extrasa inapoi in urna (rezultatul experientei este acelasi daca s-ar lua n deodata).

Se cere sa se determine probabilitatea P a evenimentului ca din cele n bile extrase, u bile extrase sa fie albe si v bile sa fie negre .

Pentru a calcula probabilitatea evenimentului cerut,vom aplica defintia clasica a probabilitatii.

Numarul cazurilor posibile, este egal cu numarul grupelor ce se pot forma cu cele a+b bile, adica grupe.

Cate cazuri favorabile sunt ?

Numarul de grupe care sa contina u bile albe, respectiv v bile negre sunt , respectiv . Deoarece pentru fiecare grupa din ,avem grupe favorabile, rezulta ca in total avem grupe favorabile, de unde

P_n(a,b;u,v) = .

Generalizand: fie o urna in care sunt a_k bile de culoarea k, k=1,2,,s; sa se determine probabilitatea evenimentului ca luand deodata n bile sa avem din fiecare culoare u_k ,k=1,,s bile.

Printr-un rationament analog celui facut in cazul a doua culori, se gaseste:

P_n(a₁,,a_s;u₁,,u_s) = .

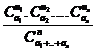b) Schema urnei cu bila revenita (binomiala sau Bernoulli)

Sa presupunem ca intr-o urna sunt bile de doua culori: albe si negre. Fie A, evenimentul de a extrage o bila alba cu probabilitatea P(A)=p; , evenimentul de a extrage o bila neagra cu probabilitatea P() =q = 1 - p .

Facandu-se n extractii succesive, introducandu-se de fiecare data in urna bila extrasa, sa se calculeze probabilitatea evenimentului X, ca din cele n bile extrase, k bile sa fie albe si n-k bile sa fie negre.

Sa notam cu A_k, evenimentul compus care consta in faptul ca in cele n probe evenimentul A se produce de k ori si evenimentul de n-k ori, adica:

A_k= cu P(A_k)=p^k.q^n-k .

Evenimentul X este o reuniune de evenimente incompatibile A_k, in numar de , deci:

P(X) = .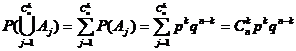

Pentru a pune in evidenta parametrii acestei probabilitati, vom scrie:

f_n(k,p) =

c) Schema polinomiala

Sa consideram acum cazul mai general, cand in urna sunt bile de s culori si se fac n extractii succesive, punand de fiecare data bila scoasa inapoi in urna.

Cunoscand ca probabilitatea evenimentului A_i, i=1,2,,s de a scoate o bila de culoarea i, este P(A_i)=p_i, se cere sa se determine probabilitatea evenimentului ca din cele n bile extrase, evenimentul A_i, i=1,,s sa se produca de k_i ori (sa apara de k_i ori bila de culoare i , i=1,2,,s).

Un rationament analog cu cel facut in cazul schemei urnei in care se afla bile de doua culori, ne conduce la relatia:

f_n(k₁,,k_s;p₁,,p_s) =

unde p₁+p₂+ +p_s = 1 si k₁ + k₂ + + k_s = n.

d) Schema urnelor Poisson

O urna Bernoulli este careacterizata prin aceea ca probabilitatea p pentru realizarea evenimentului dorit A, in timpul celor n extractii succesive este constanta (deoarece bila extrasa se pune din nou in urna). Schema lui Bernoulli, poate fi prezentata sub forma a n urne identice din care se scoate cate o bila, de unde se obtine ca probabilitatea ca din cele n bile extrase, k sa fie albe, este data de f_n(x,p).

Schema urnelor Poisson (S.D.Poisson,1781-1840, matematician francez, s-a ocupat cu analiza matematica, mecanica si probabilitati), generealizeaza schema urnei cu bila revenita considerand n urne U_i cu bile albe si negre, iar evenimentul A_i de a scoate o bila alba din urna U_i, are probabilitatea P(A_i)=p_i iar P(=q_i .

Scotandu-se din fiecare urna cate o bila, se cere sa se determine probabilitatea evenimentului X, ca din cele n bile extrase, x bile sa fie albe si n-x bile sa fie negre.

Daca se noteaza cu:

h₁ , h₂ , , h_x si k₁ , k₂ , , k_n-x

grupuri de x, respectiv n-x numere din sirul 1,2,,n, atunci un eveniment care realizeaza evenimentul cert, va fi de forma:

A_h,k =

si are probabilitatea:

P(A_h,k) =

Evenimentele A_h,k sunt grupe distincte de x evenimente A_h si n-x evenimente permutate intre ele, deci evenimentul cerut:

X =

are probabilitatea:

P_n(X) =

si se observa ca termenii sumei precedente sunt produse partiale ale dezvoltarii:

(p₁+q₁)(p₂+q₂) (p_n+q_n),

care contine x factori p_h si n-x factori q_k .

Daca se considera polinomul in t:

(p₁t+q₁)(p₂t+q₂) (p_nt+q_n) ,

atunci probabilitatea P_n(X) este tocmai coeficientul lui t^x din dezvoltarea acestui polinom.