
|
|
|
Emanoil Arghiriade - 2 ianuarie 1903
Nicolae Cioranescu - 28 martie 1903
Miron Nicolescu - 14/27 august 1903
A. N. Kolmogorov (membru de onoare al Academiei Romane) - 1903
Beniamino Segre (prieten al matematicienilor romani) - 1903
John von Neumann (cu familie avand ramificatii la Timisoara) - 1903
Gheorghe Titeica - 1873
Dimitrie Pompeiu - 1873
T. Levi-Civita (profesor al unor mari matematicieni romani) - 1873
180 de ani de la moartea lui Gh. Lazar
190 de ani de la moartea lui Lagrange
210 ani de la nasterea lui N. Lobacevski
110 ani de la nasterea lui Petre Sergescu
80 de ani de la nasterea lui C. T. Ionescu-Tulcea
70 de ani de la nasterea lui: Nicu Boboc, Aurel Cornea, Ciprian Foias, Kostake Teleman, Radu Theodorescu, Dragos Vaida
40 de ani de la moartea lui Jacques Hadamard
Articolul de fata isi propune sa aduca in fata cititorilor o problema data la faza locala in anul 1985. Deoarece aceasta inegalitate are spectru larg de aplicatii, o prezentam in continuare ca pe o lema fundamentala in rezolvarea unor probleme de geometrie elementara.
Lema (Ion Cucurezeanu). In orice triunghi ascutitunghic are loc urmatoarea inegalitate:
![]() .
.
Demonstratie. Avem ![]()
![]()
![]() , care este echivalenta cu inegalitatea din enunt.
, care este echivalenta cu inegalitatea din enunt.
Iata in continuare cateva aplicatii:
1. Sa se demonstreze ca in orice triunghi ABC are loc urmatoarea inegalitate:
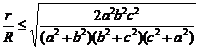 .
.
(Tudorel Lupu si Dumitru Anton, locala 1988)
Solutie. Scriind lema
de mai sus precum si inegalitatile omoloage si inmultindu-le
avem: ![]() , care inmultita cu 4R conduce la aplicatia 1.
, care inmultita cu 4R conduce la aplicatia 1.
2. Sa se arate ca in orice triunghi ascutitunghic are loc inegalitatea:
![]() .
.
(Cezar Lupu si Ovidiu Jianu)
Solutie. Aplicand ![]() si analoagele,
inegalitatea devine:
si analoagele,
inegalitatea devine: ![]() Dar tinand cont de
lema din enunt obtinem:
Dar tinand cont de
lema din enunt obtinem:
![]() , care este echivalenta cu
, care este echivalenta cu ![]() Scriind si
analoagele si adunandu-le, vom obtine ca
Scriind si
analoagele si adunandu-le, vom obtine ca ![]() , cunoscuta si sub denumirea de inegalitatea lui Hadwiger.
, cunoscuta si sub denumirea de inegalitatea lui Hadwiger.
3. In orice triunghi ascutitunghic are loc inegalitatea:
![]() .
.
(Cezar Lupu si Tudorel Lupu)
Solutie. Aplicand lema din enunt, inegalitatea de demonstrat devine:
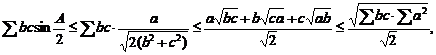 dupa care,
aplicand binecunoscuta inegalitate
dupa care,
aplicand binecunoscuta inegalitate ![]() , obtinem enuntul.
, obtinem enuntul.
4. Sa se demonstreze ca in orice triunghi ascutitunghic are loc inegalitatea:
![]() .
.
(Cristian Grecu, G.M., 1994)
Solutie. Din 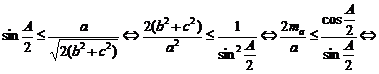
![]() , care este echivalenta in cele din urma cu ma R(1 + cos A)
, care este echivalenta in cele din urma cu ma R(1 + cos A) ![]() . Scriind si analoagele si adunandu-le, vom
obtine:
. Scriind si analoagele si adunandu-le, vom
obtine:
![]() . Aplicand si inegalitatea
. Aplicand si inegalitatea ![]() , obtinem inegalitatea dorita.
, obtinem inegalitatea dorita.
5. Sa se demonstreze ca in orice triunghi ascutitunghic are loc inegalitatea:
![]() .
.
(Dorel Mihet, R.M.T., 1985)
Solutie. Avem 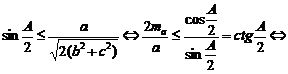
2![]() . Scriind si analoagele si adunandu-le, vom
obtine:
. Scriind si analoagele si adunandu-le, vom
obtine:
![]() inegalitatea din
enunt.
inegalitatea din
enunt.
6. In orice triunghi ascutitunghic are loc inegalitatea:
![]() . (***)
. (***)
Solutie. Avem 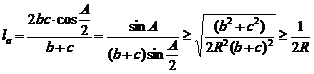 . Scriind si analoagele si adunandu-le, obtinem
enuntul.
. Scriind si analoagele si adunandu-le, obtinem
enuntul.
7. In orice triunghi ascutitunghic avem inegalitatea urmatoare:
![]() .
.
(J. M. Child, A.M.M., 1939)
Solutie. Aplicand inegalitatea lui Cauchy-Schwarz, vom obtine:
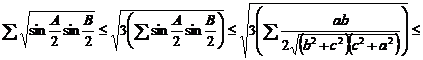
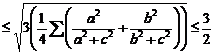 , unde am aplicat inegalitatea cunoscuta
, unde am aplicat inegalitatea cunoscuta
![]() .
.
8. Sa se arate ca in orice triunghi ABC ascutitunghic, in care I este centrul cercului inscris si R raza cercului circumscris triunghiului ABC, are loc inegalitate:
AI + BI + CI < 4R.
(C. Caragea, etapa judeteana, 1992)
Solutie. Se stie
ca 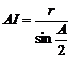 si analoagele.
Insa tinand cont ca
si analoagele.
Insa tinand cont ca ![]() vom obtine
ca
vom obtine
ca ![]()
= ![]() , q.e.d.
, q.e.d.
In continuare, vom da alte doua aplicatii pe care le lasam la indemana cititorului.
9. In orice triunghi ascutitunghic are loc urmatoarea inegalitate:
![]() .
.
(Cezar Lupu)
10. In orice triunghi ascutitunghic are loc inegalitatea urmatoare:
![]() .
.
(Cezar Lupu)
In incheiere, putem spune ca inegalitatea domnului profesor Ion Cucurezeanu are o aplicabilitate larga in ceea ce priveste relatiile ce au loc intr-un triunghi, in cazul nostru ascutitunghic.O generalizare a acestei leme este urmatoarea:
"In orice triunghi ascutitunghic ABC are loc inegalitatea:
![]() cu t I (0, 1) sau t = 2".
cu t I (0, 1) sau t = 2".
Aceasta generalizare apartine lui Ballieu. Ramane ca problema deschisa daca ea este adevarata pentru t I (1, 2).
Scopul acestei notei matematice este acela de a defini triunghiurile si suprafetele coparalele si de a prezenta unele proprietati ale acestora.
Doua triunghiuri ABC si A1B1C1 sunt coparalele daca AA1 BB1 CC1.
Doua suprafete triunghiulare ABC si A1B1C1 sunt coparalele daca pot fi
pozitionate in plan astfel incat![]() .
.
Daca ABC este un triunghi oarecare si M un punct arbitrar pe dreapta BC, atunci exista relatia
![]() , (1)
, (1)
unde d este distanta dintre paralelele la AM duse prin B si C.
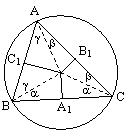
Demonstratie. Fie B si C proiectiile punctelor B si C pe dreapta AM (fig. 1).
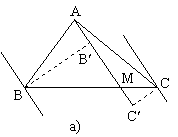 |
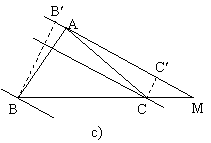
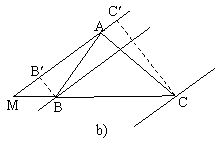
Figura 1
Daca ![]() , figura 1-a), avem:
, figura 1-a), avem:
![]() ,
,
iar daca ![]() , figurile 1-b) si 1-c), avem:
, figurile 1-b) si 1-c), avem:
![]() .
.
Fie ABC
si A1B1C1 doua triunghiuri coplanare coparalele.
Daca inaltimile varfurilor A
si A1 ale celor
doua triunghiuri sunt necongruente (![]() ), atunci exista punctele M I BC si
), atunci exista punctele M I BC si ![]() astfel incat
astfel incat
![]() (2)
(2)
si ![]() (3)
(3)
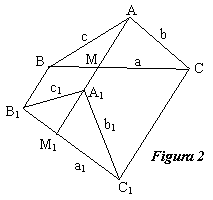
Demonstratie. Cazurile AA1 BC si AA1 B1C1
sunt excluse, deoarece fiecare dintre ele implica
![]() . Notand atunci
. Notand atunci ![]() si
si
![]() (fig. 2), din BB1 MM1 CC1
(fig. 2), din BB1 MM1 CC1
rezulta ![]() , adica relatia (2).
, adica relatia (2).
In conformitate cu lema 1, avem ![]()
si ![]() , deci
, deci ![]() ,
,
adica relatia (3).
Daca doua triunghiuri ABC si A1B1C1 sunt coplanare si coparalele, atunci
![]() , (4)
, (4)
unde a, b, c
si ![]() ,
, ![]() ,
, ![]() sunt respectiv
lungimile laturilor celor doua triunghiuri,
sunt respectiv
lungimile laturilor celor doua triunghiuri, ![]() si
si ![]() .
.
Demonstratie. Cazul ![]() . Tinand seama de lema 2, vom nota cu x valoarea rapoartelor egale din
relatia (2). Aplicand teorema lui
Stewart in triunghiul ABC (fig. 2),
avem
. Tinand seama de lema 2, vom nota cu x valoarea rapoartelor egale din
relatia (2). Aplicand teorema lui
Stewart in triunghiul ABC (fig. 2),
avem
![]() ,
,
de unde, inlocuind pe BM
si MC respectiv cu ![]() si
si ![]() , obtinem
, obtinem
![]() .
.
Tinand seama si de relatia analoaga
![]() ,
,
din (3), prin ridicare la patrat, obtinem urmatoarea ecuatie in x:
![]() . (5)
. (5)
Ecuatia (5) are radacinile reale daca si numai daca
![]()
![]() .
.
Din
aceasta inegalitate, tinand seama de relatiile: ![]() si
si ![]() , se obtine imediat inegalitatea (4).
, se obtine imediat inegalitatea (4).
Cazul ![]() . Din considerente de simetrie, inegalitatea (4) este
adevarata si in cazurile
. Din considerente de simetrie, inegalitatea (4) este
adevarata si in cazurile ![]() si
si ![]() . Ramane atunci de studiat cazul
. Ramane atunci de studiat cazul ![]() ,
, ![]() ,
, ![]() . In acest caz, cele doua triunghiuri sunt congruente,
iar inegalitatea (4) este verificata ca egalitate.
. In acest caz, cele doua triunghiuri sunt congruente,
iar inegalitatea (4) este verificata ca egalitate.
Inegalitatea (4) este adevarata si in cazul a doua triunghiuri coparalele necoplanare.
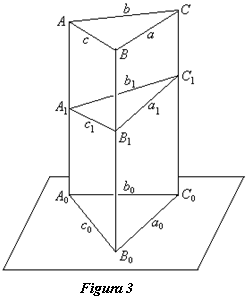 Demonstratie. Un plan perpendicular pe dreptele paralele
Demonstratie. Un plan perpendicular pe dreptele paralele ![]() ,
, ![]() ,
, ![]() (figura 3),
intersecteaza aceste drepte respectiv in punctele
(figura 3),
intersecteaza aceste drepte respectiv in punctele ![]() ,
, ![]() ,
, ![]() . Notand cu
. Notand cu ![]() ,
, ![]() ,
, ![]() lungimile laturilor
triunghiului
lungimile laturilor
triunghiului ![]() , avem:
, avem:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Scriem aceste relatii sub forma:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
unde ![]() ,
, ![]() . Utilizand aceste relatii, formula ariei unui triunghi
in functie de lungimile laturilor si notatia
. Utilizand aceste relatii, formula ariei unui triunghi
in functie de lungimile laturilor si notatia ![]() , avem:
, avem:
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
Din aceste trei relatii, rezulta
![]()
![]() .
.
Mai departe, efectuand inlocuirile ![]() si
si ![]() , obtinem
, obtinem
![]()
![]() ,
,
adica inegalitatea ceruta.
Lasam in seama cititorilor demonstrarea urmatorului rezultat important:
Doua suprafete triunghiulare ABC si A1B1C1 sunt coparalele daca si numai daca se verifica inegalitatea (4) de la teorema 1.
Doua suprafete triunghiulare cu aceeasi arie sunt coparalele.
Demonstratie. Pentru S = S1, inegalitatea (4) se transforma in cunoscuta inegalitate a lui Pedoe
![]() .
.
10. Doua suprafete triunghiulare ABC si A1B1C1 cu BC = B1C1 sunt coparalele.
Indicatie. Se aduce inegalitatea (4) la forma ![]() .
.
20. Doua suprafete triunghiulare ABC si A1B1C1 cu ![]() sunt coparalele.
sunt coparalele.
Indicatie. Se aduce inegalitatea (4) la forma ![]() , unde D si D1 sunt picioarele
inaltimilor din A si A1 in cele doua
triunghiuri, sau se pozitioneaza cele doua suprafete
triunghiulare astfel incat dreptele BC
si B1C1 sa coincida, iar
punctele A si A1 sa fie de
aceeasi parte.
, unde D si D1 sunt picioarele
inaltimilor din A si A1 in cele doua
triunghiuri, sau se pozitioneaza cele doua suprafete
triunghiulare astfel incat dreptele BC
si B1C1 sa coincida, iar
punctele A si A1 sa fie de
aceeasi parte.
30. Suprafata
triunghiulara ABC cu m( A) = ![]() si suprafata
triunghiulara A1B1C1 sunt coparalele daca si numai daca
si suprafata
triunghiulara A1B1C1 sunt coparalele daca si numai daca
![]() .
.
40. Suprafata triunghiulara ABC si suprafata triunghiulara echilaterala A1B1C1 cu lungimea laturilor l1 sunt coparalele daca si numai daca
![]() .
.
50. Suprafata
triunghiulara ABC si
suprafata triunghiulara echilaterala A1B1C1 cu lungimea laturilor ![]() sau
sau ![]() sunt coparalele.
sunt coparalele.
60. Suprafata triunghiulara ABC si suprafata triunghiulara A1B1C1 cu
![]() ,
, ![]() ,
, ![]()
sunt coparalele (ma, mb, mc fiind lungimile medianelor triunghiului ABC).
La inceputul secolului al XX-lea, intreaga evolutie anterioara a analizei a permis introducerea si dezvoltarea puternica a teoriei spatiilor metrice, ale carei notiuni fundamentale au fost formulate in 1906 in [4] de catre matematicianul francez M. Fréchet. Cf. Dieudonné [2], "pentru a desprinde proprietatile legate de obiectele studiate, Fréchet a avut ideea geniala de a nu specifica neaparat natura acestor obiecte, ci de a studia o anumita multime, pe care este definita o functie distanta intre doua elemente arbitrare, cu valori nenegative si verificand trei dintre proprietatile clasice ale distantei euclidiene".
O multime E se numeste spatiu metric daca fiecarei perechi de elemente x, y I I E i s-a asociat un numar real d(x, y) astfel incat sunt indeplinite conditiile:
1) d(x, y) 0 pentru orice x, y I E si d(x, y) = 0 daca si numai daca x = y;
2) d(x, y) = d(x, y) pentru orice x, y I E (proprietatea de simetrie);
3) d(x, z) d(x, y) + d(y, z) pentru orice x, y, z I E (inegalitatea triunghiului).
Functia d : E E R se numeste metrica, iar d(x, y) semnifica distanta intre punctele x si y.
Exemple: (i) Orice multime E de pe axa reala R este un spatiu metric in raport cu distanta d(x, y) = x - y In mod analog, orice submultime E a spatiului euclidian Rn poate fi privita ca spatiu metric inzestrat cu "metrica euclidiana"
d(x, y)
= ![]() ,
,
unde x = (x1, x2, ., xn), y = (y1, y2, ., yn).
(ii) Cercul S1 = este un spatiu metric, distanta dintre doua puncte fiind cea mai mica dintre lungimile arcelor determinate de cele doua puncte de pe cerc.
Majoritatea multimilor de functii intalnite in problemele de analiza pot fi inzestrate cu "distante" definite in concordanta cu problemele studiate. De pilda, multimea C[0, l] a tuturor functiilor continue u : [0, l] R este un spatiu metric, distanta dintre functiile u si v fiind definita prin
(1) d(u,
v) = ![]() u(t)
- v(t)
u(t)
- v(t)
In lucrarile legate de problemele de tip Sturm-Liouville sau in studiile de teoria probabilitatilor este mai utila metrica
d(u, v) = ![]()
care defineste un alt spatiu functional deosebit de important, notat cu L2(0,1).
Daca (E, d)
este un spatiu metric, se numeste bila deschisa de raza r > 0 si centru x0 I E multimea B(x0 r) = . Notinea
corespunzatoare de bila
inchisa ![]() x0 r) de raza r > 0 si centru x0 se obtine inlocuind in
definitia bilei deschise semnul "<" cu " ". O multime A E este deschisa daca pentru orice x0 I A exista o bila deschisa centrata in x0 si continuta in A.
O multime A E este inchisa daca complementara sa
este deschisa. O multime A dintr-un
spatiu metric (E, d) se numeste densa daca orice bila deschisa centrata
intr-un punct din E contine cel
putin un punct din A. De
pilda, multimea numerelor rationale este densa in
multimea R a numerelor reale,
iar multimea (r1, ., rn) a punctelor de coordonate
rationale este densa in spatiul euclidian n-dimensional.
x0 r) de raza r > 0 si centru x0 se obtine inlocuind in
definitia bilei deschise semnul "<" cu " ". O multime A E este deschisa daca pentru orice x0 I A exista o bila deschisa centrata in x0 si continuta in A.
O multime A E este inchisa daca complementara sa
este deschisa. O multime A dintr-un
spatiu metric (E, d) se numeste densa daca orice bila deschisa centrata
intr-un punct din E contine cel
putin un punct din A. De
pilda, multimea numerelor rationale este densa in
multimea R a numerelor reale,
iar multimea (r1, ., rn) a punctelor de coordonate
rationale este densa in spatiul euclidian n-dimensional.
Notiunile fundamentale de convergenta, continuitate etc., stabilite pentru axa reala, se transpun corespunzator in contextul mai general al spatiilor metrice. Vom reaminti doar definitiile si proprietatile de care vom avea nevoie in vederea enuntarii si demonstrarii rezultatului principal al acestei note.
Fie (E, d)
un spatiu metric. Un sir (xn) de puncte din E se numeste convergent catre
un punct x I E daca pentru orice e > 0 exista un numar natural Ne astfel incat
pentru orice n > Ne are loc inegalitatea d(x, xn) e Daca (E, d1) si (F, d2) sunt
spatii metrice, atunci o functie u
: E F se
numeste continua in punctul x0 I E daca
pentru orice e > 0 exista d > 0 astfel incat din conditia d1(x, x0) < d sa rezulte
d2( f (x), f (x0)) < e O functie continua in orice punct din E se numeste continua pe E. Una dintre cele mai simple functii
continue este aplicatia u : E R
definita prin u(x)
= d(x, x0), unde (E, d) este un spatiu
metric si x0 I E. Acest lucru rezulta cu usurinta din
inegalitatea triunghiului.
Sirul (xn) din spatiul metric (E,
d) se numeste sir fundamental (sir Cauchy) daca pentru orice e > 0
exista un numar natural Ne astfel incat pentru orice n Ne si
m Ne are loc inegalitatea d(xn, xm) e Folosind inegalitatea triunghiului, deducem ca orice
sir convergent este un sir fundamental. Reciproca acestei
proprietati nu este adevarata. Intr-adevar, fie
multimea E = (0, 1)
inzestrata cu metrica uzuala a axei reale. In acest spatiu
metric, sirul xn = ![]() (n 1) este un
sir fundamental care nu este convergent. Acest exemplu impune introducerea
urmatoarei clase importante de spatii metrice. Un spatiu metric
(E, d) se numeste complet daca orice sir
fundamental din E este convergent
catre un element din E. Spatiile
metrice complete sunt caracterizate de urmatoarea proprietate a bilelor inchise, cunoscuta sub numele de principiul lui Cantor, un spatiu
metric este complet daca si numai daca orice sir descendent
de bile inchise nevide, de diametru tinzand catre zero, are un punct
comun.
(n 1) este un
sir fundamental care nu este convergent. Acest exemplu impune introducerea
urmatoarei clase importante de spatii metrice. Un spatiu metric
(E, d) se numeste complet daca orice sir
fundamental din E este convergent
catre un element din E. Spatiile
metrice complete sunt caracterizate de urmatoarea proprietate a bilelor inchise, cunoscuta sub numele de principiul lui Cantor, un spatiu
metric este complet daca si numai daca orice sir descendent
de bile inchise nevide, de diametru tinzand catre zero, are un punct
comun.
O proprietate foarte interesanta a spatiilor metrice complete, cu implicatii profunde in multe directii, este o teorema demonstrata independent in 1898 de Osgood pentru axa reala si in 1899 de catre Baire [1] pentru Rn: daca (E, d) este un spatiu metric complet si (Un) este un sir de multimi deschise si dense in E, atunci intersectia lor este, de asemenea, densa in E. In contextul general al spatiilor metrice complete, aceasta proprietate este cunoscuta sub numele de lema lui Baire. O frumoasa aplicatie a acestui rezultat a fost gasita in 1931 de catre Banach, care a aratat ca "majoritatea" functiilor continue u : [0, 1] R nu au derivata la dreapta in nici un punct. Intr-adevar, observam ca multimea C[0, 1] devine un spatiu metric complet in raport cu distanta definita in relatia (1). Pentru orice intreg n l, fie Fn multimea functiilor u : [0, 1] R cu proprietatea ca exista x (care depinde de u) astfel incat
0 x 1 - ![]() si u(x ) - u(x) n(x - x), x x x +
si u(x ) - u(x) n(x - x), x x x + ![]() .
.
Multimea Fn este inchisa in C[0, 1], deci complementara sa Un
este deschisa. In plus, multimea Un este densa. Aceasta rezulta din faptul
ca pentru orice u I C[0, 1] si pentru orice M > 0 si e > 0,
exista o functie v I C[0, 1] astfel incat d(u, v)
< e, iar derivata la dreapta a lui v exista in orice punct si este cel putin M in valoare absoluta. Pentru
aceasta e suficient sa luam o curba tip dinti de fierastrau, al carei grafic este
situat intr-o banda de latime e in jurul graficului lui u, iar numarul de "dinti" sa fie suficient de mare
astfel incat fiecare segment ce compune graficul sa aiba o panta
mai mare ca M sau mai mica decat
-M. Conform lemei lui Baire,
multimea U = ![]() este densa in C[0,
1]. Folosind acum definitia multimilor Fn, rezulta ca orice functie u I U nu poate avea
derivata la dreapta finita in nici un punct din intervalul [0,1]. In
1881 Volterra a demonstrat un rezultat in aceeasi directie ca acela
al lui Baire si Osgood. Mai precis, Volterra a aratat ca
daca doua functii definite pe R cu valori reale sunt continue pe submultimi dense ale lui R, atunci multimea punctelor
comune de continuitate este densa in R.
Acest rezultat a fost publicat in [6], iar demonstratia sa este
reamintita in [3]. Scopul acestei note este de a prezenta o generalizare a
rezultatului lui Volterra in contextul spatiilor metrice complete,
aratand in plus ca multimea
punctelor comune de continuitate nu este numarabila. In
particular, o functie u : R R nu poate fi
continua doar in punctele rationale. Mai precis, vom demonstra
urmatorul rezultat.
este densa in C[0,
1]. Folosind acum definitia multimilor Fn, rezulta ca orice functie u I U nu poate avea
derivata la dreapta finita in nici un punct din intervalul [0,1]. In
1881 Volterra a demonstrat un rezultat in aceeasi directie ca acela
al lui Baire si Osgood. Mai precis, Volterra a aratat ca
daca doua functii definite pe R cu valori reale sunt continue pe submultimi dense ale lui R, atunci multimea punctelor
comune de continuitate este densa in R.
Acest rezultat a fost publicat in [6], iar demonstratia sa este
reamintita in [3]. Scopul acestei note este de a prezenta o generalizare a
rezultatului lui Volterra in contextul spatiilor metrice complete,
aratand in plus ca multimea
punctelor comune de continuitate nu este numarabila. In
particular, o functie u : R R nu poate fi
continua doar in punctele rationale. Mai precis, vom demonstra
urmatorul rezultat.
Fie (E, d1) un spatiu metric complet si (F, d2) un spatiu metric. Fie doua aplicatii u, v : E F. Notam cu Cu si Cv multimile punctelor de continuitate ale lui u si v si presupunem ca aceste multimi sunt dense in E. Atunci Cu Cv este o multime densa in E. In plus, daca E nu este o multime numarabila, atunci Cu Cv este nenumarabila.
O conditie suficienta ca un spatiu metric complet (E, d) sa nu fie numarabil (a se vedea Silov [5]) este ca multimea E sa fie fara puncte izolate. Reamintim ca un punct x0 se numeste izolat daca exista o bila centrata in xq care sa nu contina nici un punct al multimii E diferit de x0. Rezultatul de mai sus afirma in particular ca daca multimea punctelor de continuitate ale unei functii u : R R este densa in R, atunci aceasta multime nu este numarabila. Gandul ne poarta aici catre functia lui Riemann care este continua pe multimea numerelor irationale.
Demonstratia teoremei. Fie C = o submultime numarabila arbitrara a lui E. Observam ca, pentru a incheia demonstratia, este suficient sa aratam ca
(2) B(a, r) Cu Cv C
pentru orice a I E si orice r > 0, unde B(a, r) semnifica bila deschisa din E cu centrul a si de raza r. Intr-adevar, daca (2) este indeplinita, atunci B(a,r) Cu Cv deci Cu Cv este o submultime densa a lui E. Relatia (2) implica si faptul ca multimea Cu Cv nu este numarabila. Intr-adevar, presupunand contrariul, putem alege C = Cu Cv, deci B(a, r) Cu Cv C = , ceea ce contrazice (2). Pentru a I I E si r > 0 fixati, fie a0 = a si r0 = r. Definim inductiv sirurile (an)n 0 > 0 E si (rn)n 0 R+ cu urmatoarele proprietati:
(i) ![]() (an+1, rn+1) B(an, rn), pentru orice n 0;
(an+1, rn+1) B(an, rn), pentru orice n 0;
(ii) cn B(an, rn), pentru orice n > 1;
(iii) daca n este impar, atunci d2(u(x), u(y)) < l/n, pentru orice x, y I B(an, rn);
(iv) daca n 2 este par, atunci d2(v(x), v(y)) < l/n, pentru orice x, y I B(an, rn).
Aceste
siruri sunt construite astfel: am definit deja a0 si r0.
Presupunem ca am definit ak
si rk, pentru orice k < n. Daca n este impar, alegem an
I B(an-1, rn-1) Cu.
Observam ca un asemenea element exista intrucat multimea Cu este densa in E. Folosind acum continuitatea lui u in an,
exista d > 0 astfel incat d2(u(x), u(an)) <
< ![]() , daca d1(x,
an) < d Alegand acum rn > 0
astfel incat
, daca d1(x,
an) < d Alegand acum rn > 0
astfel incat
rn < min![]() , rezulta ca daca x, y I B(an, rn),
atunci
, rezulta ca daca x, y I B(an, rn),
atunci
d2(u(x),
u(y)) d2(u(x), u(an)) + d2(u(an), u(y)) < ![]() .
.
Observam, de asemenea,
ca ![]() (an, rn) B(an-1, rn-1).
Intr-adevar, daca d1(x, an) rn, atunci
(an, rn) B(an-1, rn-1).
Intr-adevar, daca d1(x, an) rn, atunci
d1(x, an-1) d1(x, an) + d1(an, an-1) rn + d1(an, an-1) < rn-1,
adica x I B(an-1,
rn-1).
Daca n este par, construim
similar an si rn, cu singura
observatie ca inlocuim u
(resp. Cu) cu v (resp. Cv). Deoarece E
este spatiu complet si (rn)
este un sir convergent la zero, putem aplica principiul lui Cantor.
Asadar, exista
b I ![]() . Mai mult,
deoarece
. Mai mult,
deoarece ![]() (an+1, rn+1) B(an, rn), deducem ca b
I I B(an, rn), pentru orice n 0.
(an+1, rn+1) B(an, rn), deducem ca b
I I B(an, rn), pentru orice n 0.
Aratam in continuare ca functiile u si v sunt continue in b, adica b I Cu Cv. Pentru e > 0 fixat, alegem un intreg impar N astfel incat 1/N < e Folosind (iii), rezulta ca daca d < rN - d1(b, aN), atunci d2(u(x), u(b)) < 1/N < e, daca d1(x, b) < d Aceasta probeaza continuitatea lui u in b. In mod similar deducem ca b I Cv. Deoarece b I B(an, rn) si cn B(an, rn), pentru orice n l, rezulta ca b C, adica relatia (2) este demonstrata. Cu aceasta, demonstratia teoremei este incheiata.
[1] R. Baire, Sur les fonctions de variables réelles, Annali di Mat. 3(III) (1899), 1-123.
[2] J. Dieudonné, Abregé d'histoire des mathématiques, Hermann, Paris, 1986.
[3] W. Dunham, A historical gem from Vito Volterra, Math. Magazine 63 (1990), 234-237.
[4] M. Frechét, Sur quelques points du calcul fonctionnel, Rend. Circ. Mat. Palermo XXII (1906), 1-74.
[5] G. E. Silov, Analiza matematica, Editura Stiintifica si Enciclopedica, Bucuresti, 1989.
[6] V. Volterra, Alcune osservasioni sulle funzioni punteggiate discontinue, Giornale di Matematiche 19 (1881), 76-86.
Tratam
in aceasta nota o serie de proprietati ale sirului an =![]() pentru an = n2
+ n. Fie deci a1 =
pentru an = n2
+ n. Fie deci a1 = ![]() si an =
si an = ![]() pentru n 2 vom arata ca:
pentru n 2 vom arata ca:
1) [an] = n, unde [x] reprezinta partea intreaga a lui x;
2) an este strict crescator si ![]() an =
an =
3) n 1 este convergent, unde reprezinta partea fractionara a lui x;
4) ![]() = 1;
= 1;
5) ![]() = 0.
= 0.
Solutie 1) Vom arata ca: n an < n + 1,
n I N* prin inductie. Pentru n = 1 obtinem
1 ![]() < 2. Presupunem ca n - 1 an-1 < n
si aratam ca n an < n + 1. Din an-1 n - 1,
< 2. Presupunem ca n - 1 an-1 < n
si aratam ca n an < n + 1. Din an-1 n - 1,
adunand n2 + n, obtinem: n2 + n + an-1 n2 + 2n - 1 > n2 si deci an =
=![]() n; analog din an-1
< n obtinem n2 + n + an-1
< n2 + 2n < n2 + 2n + 1
si deci an < n + 1, adica am aratat ca
[an] = n.
n; analog din an-1
< n obtinem n2 + n + an-1
< n2 + 2n < n2 + 2n + 1
si deci an < n + 1, adica am aratat ca
[an] = n.
2)
Din an n obtinem ![]() an = , iar din sirul de inegalitati n an < n + 1 an+1
< <
n + 2 deducem ca (an)n 1 este strict
crescator.
an = , iar din sirul de inegalitati n an < n + 1 an+1
< <
n + 2 deducem ca (an)n 1 este strict
crescator.
3)
Din
inegalitatea n an < n + 1 obtinem 0 an - n < 1, adica sirul este marginit. Aratam
ca sirul n 1 este strict crescator, adica > 0. Avem urmatorul sir de
echivalente: > 0 an+1
- (n + 1) - an + n > 0 ![]() > an
+ 1 n2 + 3n + 2 + an
>
> an
+ 1 n2 + 3n + 2 + an
> ![]() + 2an +
1
+ 2an +
1 ![]() + an - n2
- 3n - 1 < 0; aceasta
inseamna ca an
este intre radacini si cum an
> 0 ramane sa aratam ca: an <
+ an - n2
- 3n - 1 < 0; aceasta
inseamna ca an
este intre radacini si cum an
> 0 ramane sa aratam ca: an < ![]() . Vom arata acest fapt prin inductie
matematica. Pentru n = 1
obtinem:
. Vom arata acest fapt prin inductie
matematica. Pentru n = 1
obtinem: ![]()
![]() + 1 <
+ 1 <
<![]() , care este adevarata. Presupunem
, care este adevarata. Presupunem ![]() si arat
ca
si arat
ca
![]() . La presupunerea facuta adunam n2 + n si apoi trecand la radical obtinem:
. La presupunerea facuta adunam n2 + n si apoi trecand la radical obtinem: 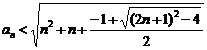 . Vom arata ca:
. Vom arata ca:
![]() . Prin ridicare la patrat si aducere la
acelasi numitor obtinem:
. Prin ridicare la patrat si aducere la
acelasi numitor obtinem: ![]() < 4n + 4, care se obtine adunand
inegalitatile evidente:
< 4n + 4, care se obtine adunand
inegalitatile evidente: ![]() < 2n + 1 si
< 2n + 1 si
![]() < 2n + 3. Am aratat ca sirul
n 1 este strict crescator.
< 2n + 3. Am aratat ca sirul
n 1 este strict crescator.
4) Din an n
obtinem an-1
n - 1; adunam n2 + n,
extragem radicalul, apoi scadem n
si avem: ![]() si trecand la
limita
si trecand la
limita ![]() 1; dar < 1 si deci
1; dar < 1 si deci ![]() = 1.
= 1.
5) ![]()
= ![]() ; dar n an
< n + 1 si adunand n + 1 apoi inversand obtinem:
; dar n an
< n + 1 si adunand n + 1 apoi inversand obtinem: ![]() , adica:
, adica: ![]() si trecand la
limita
si trecand la
limita ![]() = 0.
= 0.
Observatie: Avand
sirul ![]() pentru a = k(k + 1), k I N*
sau a =
pentru a = k(k + 1), k I N*
sau a =
= n2, n I N*
regasim problemele propuse de prof. Maria Mihet si prof. univ. dr. Laurentiu
Panaitopol din [1].
[1]. R.M.T. nr. 4/2002
[2]. Revista "Arhimede", Nr. 1-8/2002
[3]. Ion Chitescu, Petrus Alexandrescu, Marius Radulescu, Sorin Radulescu, Analiza matematica. Clasa a XI-a; Clasa a XII-a, Editura Paralela 45.
In numarul 1-2/2003 al revistei am publicat programa oficiala pentru pregatirea examenului de definitivare in invatamant, obtinerea gradului didactic II si a concursul de titularizare a profesorilor. Mentionam ca temele marcate cu * reprezinta continuturi obligatorii pentru gradul didactic II si concursul de titularizare. Toate celelalte teme sunt comune.
In acest numar publicam un model de astfel de test, in conformitate cu actualele cerinte, si care se va dovedi deosebit de util celor care pregatesc examenele sus-mentionate.
prof. Dorin Popovici, prof. Costel Chites, prof. Gabriela Streinu-Cercel
1. Fie E = si k
numarul de triplete (A, B, C)
pentru care A B
C =
= E. Atunci:
a) k = 3n - 2; b) k = 32n - 2; c) k = 7n; d) k = 6n + 1.
2. Se considera functiile f, g : R R, f (x) = x3 + 3x,
g(x) = ![]() . Atunci:
. Atunci:
a) g nu este surjectiva; b) g nu este injectiva; c) f o g g o f ; d) f o g = g o f.
3. Fie l = ![]() . Atunci:
. Atunci:
a) 2; b) + ; c) ![]() ; d) 1.
; d) 1.
4. Numarul structurilor de grup pe o multime cu 4 elemente este:
a) 2; b) 4; c) 12; d) 16.
5. Care dintre perechile de grupuri sunt izomorfe:
a) (Q![]() , )
si (Z[X], +); b) (Z[X],
+) si (Q[X], +); c) (Z[X],
+) si (Z, +);
, )
si (Z[X], +); b) (Z[X],
+) si (Q[X], +); c) (Z[X],
+) si (Z, +);
d) (Q, +) si (Q[X], +).
6. Afirmatia adevarata este:
a) Exista grupuri finite ce contin elemente de ordin infinit.
b) Nu exista grupuri infinite cu elemente de ordin finit.
c) Exista grupuri infinite in care orice element este de ordin finit.
d) Orice grup infinit contine elemente de ordin finit 2.
7. Fie l = ![]() . Atunci:
. Atunci:
a) l = 1; b) l = 0; c) l = ln 2; d) l
8. Fie f, g I C[X], f = X91 - 1, g = X143 - 1. Atunci d = (f, g) = cel mai mare divizor comun al polinoamelor f si g este:
a) X - 1; b) 1; c) f g; d) X13 - 1.
9. Fie f,
g : R R functii
ce admit ca primitive pe F respectiv G cu proprietatile: f = ![]() (G + g), g =
(G + g), g = ![]() (F + f ), f (0) = 0, g(0) = 2. Atunci f (1) + g(1) are valoarea: a) 2; b) 1; c) 4; d) 2e.
(F + f ), f (0) = 0, g(0) = 2. Atunci f (1) + g(1) are valoarea: a) 2; b) 1; c) 4; d) 2e.
10. Fie functia f : R R ce verifica conditia f 3(x) + f (x) = x, x I R. Atunci:
a) f nu este integrabila pe intervalul
[0, 2]; b) ![]() ;
;
c) f este nemonotona; d) nu exista functii cu proprietatea din enunt.
11. Fie m, n
I N*
si ![]() . Atunci S este:
. Atunci S este:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() .
.
12. Fie 1, e1 e2 en-1
radacinile ecuatiei Xn
= 1 si ![]() . Atunci:
. Atunci:
a) T = ![]() ; b) T =
; b) T = ![]() ; c) T =
; c) T = ![]() ; d) T =
; d) T = ![]() .
.
13. Proiectia punctului A(2, 1, 1) pe planul de ecuatie x + y + 3z + 5 = 0 este:
a) (1, 0, -2); b) (-11, 0, 2); c) (-9, 1, 1); d) (-7, -1, 1).
14. Sistemul: 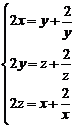 admite in R:
admite in R:
a) 4 solutii; b) o unica solutie; c) 2 solutii; d) 6 solutii.
15. Se considera multimea A = . Atunci:
a) A este nemarginita; b) inf A
= 0; c) max A = ![]() ; d) min A = 1.
; d) min A = 1.
16. Se considera a, b I R si functia continua f : R R ce verifica relatia:
f (a - x) + f (a + x) = 2b, x I R. Daca I = ![]() , atunci:
, atunci:
a) I = a
b; b) I
= 2ab; c) I
= 4ab; d) I
= ![]() .
.
17. Valoarea reala a lui a I R pentru care ecuatia diferentiala y - 5y + 6y =
= a [x] + x2 admite cel putin o
solutie y: [-1, 3] R este:
a) 0; b) 1; c) -1; d) 2.
18. Fie a = ![]() . Gradul minim al unui polinom nenul f I Z[X] ce admite pe a ca radacina este:
. Gradul minim al unui polinom nenul f I Z[X] ce admite pe a ca radacina este:
a) 12; b) 9; c) 6; d) 3.
19. Fie functia f : [0, 4] R, f (x) = ![]() . Atunci:
. Atunci:
a) f este strict monotona; b) f este strict descrescatoare pe [0, 2] si strict crescatoare pe [2, 4]; c) f este strict crescatoare pe [0, 2] si strict descrescatoare pe [2, 4]; d) f este derivabila.
20. In multimea Z Z ecuatia x(x - 1) + y(y + 3) = 10 are:
a) o infinitate de solutii; b) 4 solutii; c) 8 solutii; d) 12 solutii.
21. Fie a si b solutiile ecuatiei x2 + 3x + 1 = 0. Atunci a8 b8 are valoarea:
a) 1207; b) 2209; c) 209; d) 2207.
22. Fie a
> 0 fixat, xn > 0, n 1 astfel incat ![]() . Valorile pe care seria
. Valorile pe care seria ![]() le poate lua sunt:
le poate lua sunt:
a) (0, a); b) (0, a2); c) (a, a2); d) (0, a2].
23. Se considera planele de ecuatii: x + 2y - 2z + 3 = 0; 3x + 4y + 12z - 1 = 0. Atunci cosinusul unghiului diedru format de cele doua plane este egal cu:
a) ![]() ; b) -
; b) -![]() ; c)
; c) ![]() ; d) -
; d) -![]() .
.
24. Se considera multimea A = . Atunci numarul de elemente este:
a) 100; b) 98; c) 99; d) 97.
25. Fie d
= 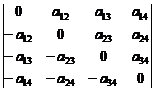 . Atunci exista aij
I Z astfel
incat:
. Atunci exista aij
I Z astfel
incat:
a) d = 7; b) d = 6; c) d = 8; d) d = 25.
26. Ecuatia planului care trece prin intersectia planelor x - 2y - 3z + 2 = 0;
4x + y + 5z + 1 = 0 si este paralel cu Oz este:
a) 17x - 7y + 13 = 0; b) x - y + 5 = 0; c) 2x + y - 7 = 0; d) 17x + 7y - 13 = 0.
27. Intr-un reper ![]() din spatiu se
considera vectorii
din spatiu se
considera vectorii 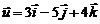 si
si ![]() , atunci proiectia lui
, atunci proiectia lui ![]() pe directia
vectorului
pe directia
vectorului ![]() este egala cu:
este egala cu:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() .
.
28. Numarul de generatori distincti ai grupului (Z14, +) este:
a) 7; b) 6; c) 13; d) 2.
29. Fie functiile f, g : [a, b] R. Atunci:
a) Daca f este integrabila si ![]() = 0, atunci f = 0.
= 0, atunci f = 0.
b) Daca f este integrabila si ![]() > 0 T f (x) 0, x I [a, b].
> 0 T f (x) 0, x I [a, b].
c) Daca f este continua, f 0 si ![]() = 0, atunci f = 0.
= 0, atunci f = 0.
d) Daca f este integrabila, atunci f este integrabila.
30. Numarul de automorfisme al corpului (C, +, ) este:
a) 1; b) 4; c) 2; d) o infinitate.
1. c); 2. d); 3. c); 4. d); 5. a); 6. c); 7. c); 8. d) 9. d); 10. b); 11. a); 12. b); 13. a);
14. c); 15. c); 16. b); 17. a); 18. c) 19. c); 20. d); 21. d); 22. b); 23. b); 24. c); 25. d); 26. a); 27. c); 28. b) 29. c); 30. c).
1.
k
= ![]() ; 2. Se arata ca f este bijectiva si ca g = f
-1;
; 2. Se arata ca f este bijectiva si ca g = f
-1;
3.
![]() 4. G = 4 T G
j Z4 sau G j K;
4. G = 4 T G
j Z4 sau G j K;
Aut k = 6, iar Aut Z4 = 2. Deci numarul de structuri este ![]() ; 6. D
=
; 6. D
= ![]() este un grup infinit
in care orice element este de ordin finit; 7. l =
este un grup infinit
in care orice element este de ordin finit; 7. l = ![]()
- ![]() ; 0
; 0 ![]() . Deci l = ln 2; 8. U91 U143 =
. Deci l = ln 2; 8. U91 U143 =
= U13; 9. f + g = F + G T f
(x) + g(x) = kex T k
= 2; f (1) + g(1) = 2e; 10. Fie f (x) < f (y)
T x < y T f este monotona T f
integrabila pe [0, 2]. Fie g(x) = x3
+ x, g : R R,
g este bijectiva; g( f
(x)) = x T f
(g(x)) = x. Notam x3 + x = t; ![]()
![]()
= ![]() ; 11. Se integreaza in doua moduri I =
; 11. Se integreaza in doua moduri I = ![]() ; 12. Fie g =
; 12. Fie g =
= xn-1 + xn-2 + . + x + 1 = ![]() . Deci T =
. Deci T = ![]() ; 14. Doua solutii: (
; 14. Doua solutii: (![]() si
si ![]() ; 16.
; 16. ![]() ; in prima integrala facem substitutia y = a - x, iar in a doua t = a + x T I
= 2ab; 20. Ecuatia
data reprezinta un cerc de centru C
; in prima integrala facem substitutia y = a - x, iar in a doua t = a + x T I
= 2ab; 20. Ecuatia
data reprezinta un cerc de centru C![]() si raza R
=
si raza R
= ![]() . Fie ABCD
patratul circumscris cercului care are laturile paralele cu axa de
coordonate;
. Fie ABCD
patratul circumscris cercului care are laturile paralele cu axa de
coordonate; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Solutiile se afla pe suprafata
patratica A B C D , unde A (4, 2), B (-3, 2), C (-3, -5), D (4, -5). Se verifica doar 12
solutii;
. Solutiile se afla pe suprafata
patratica A B C D , unde A (4, 2), B (-3, 2), C (-3, -5), D (4, -5). Se verifica doar 12
solutii;
22. 0 < ![]() < (x1 + x2 + . + xn)2
< (x1 + x2 + . + xn)2
![]() . Reciproc, fie x1
= q x0,
x2 = q2 x0,
., xn = qn x0,
q < 1;
. Reciproc, fie x1
= q x0,
x2 = q2 x0,
., xn = qn x0,
q < 1; ![]() ;
; ![]()
![]() . Deci
. Deci ![]() ;
;
23. j = ![]() ; 25. d
= (a12 a34
+ a13 a24
+ a14 a23)2
pentru
; 25. d
= (a12 a34
+ a13 a24
+ a14 a23)2
pentru
a42 = -a24. Pentru a12 = a13 = a14
= 1, a34 = a23 = 2 si a24 = -1 se obtine d = 25; 26. Planul cautat este
de forma: x - 2y - 3z + 2 + l(4x +
y + 5z + 1) = 0. Pentru ca el
sa fie paralel cu Oz,
coeficientul lui z trebuie sa
fie nul T -3 + 5l = 0 T l = ![]() . Ecuatia cautata va fi:
. Ecuatia cautata va fi:
17x - 7y + 13 = 0; 28.
Generatorii sunt numere intregi prime cu 14 in Z: 1, 3, 5, 9, 11, 13; 30. f
(x) = x, x I R;
f (a + bi) = f (a) + f
(i) f
(b) = a + b f (i); f (i2) = ( f (i))2 = f (-1) =
= -1 T f (i)
I . Deci f (a + bi) = a + bi sau f (a + bi) = a - bi, adica f (z) = z,
z I C
sau f (z) = ![]() , z I C.
, z I C.
1. Proiectarea unei unitati de invatare presupune parcurgerea, intr-o succesiune logica, a unui set de intrebari caruia ii corespunde un set de elemente ale procesului didactic:
A. In ce scop voi face?
1. Identificarea obiectivului de referinta/ competentelor specifice.
B. Ce voi face?
2. Selectarea continutului.
C. Cu ce voi face?
3. Analiza resurselor.
D. Cum voi face?
4. Determinarea activitatilor de invatare.
E. Cat s-a realizat?
5. Stabilirea instrumentelor de evaluare.
Care este corespondenta corecta intre cele doua coloane?
a. A1, B2, C3, D4, E5;
b. A1, B3, C4, D2, E5;
c. A5, B4, C1, D2, E3;
d. A4, B2, C3, D1, E5.
2. Competentele generale se definesc pe obiect de studiu si se formeaza pe durata:
a. invatamantului liceal;
b. unui an scolar;
c. unui semestru;
d. invatamantului obligatoriu.
3. Competentele specifice se definesc pe obiect de studiu si se formeaza pe durata:
a. invatamantului liceal;
b. unui an scolar;
c. unui semestru;
d. invatamantului obligatoriu.
4. Precizati ordinea in care
apar in programa scolara pentru clasele V-IX
urmatoarele componente:
A. Continuturi; B. Nota de prezentare;
C. Obiectivele de referinta; D. Obiectivele cadru;
E. Exemple de activitati de invatare.
a. A, B, C, D, E;
b. B, A, C, D, E;
c. B, D, C, E, A;
d. B, C, D, E, A.
5. Cele trei tipuri de programe: M1, M2 si M3 isi propun formarea:
a. unor competente generale diferite;
b. acelorasi competente generale diferite;
c. acelorasi competente specifice;
d. acelorasi competente.
6. Tema "Lecturi grafice" se studiaza la:
a. M1;
b. M1, M2 si M3;
c. M2, M3;
d. M3.
7. Alege itemii duali dintre urmatorii itemi:
a. Daca rezultatul este adevarat incercuieste litera A, in caz contrar, incercuieste litera F.
xn - l = (x - 1)(xn-1 + xn-2 + . + x + 1) A F
b. Inscrie in spatiul din fata fiecarui numar din
coloana I, litera din coloana II
care indica formula corecta:
I II
1) Aria dreptunghiului A. 2(L + l)
2) Perimetrul dreptunghiului B. (a + b) / 2
3) Media aritmetica a doua numere C. ![]()
4) Media proportionala a doua numere D. L l
c. Se considera numarul real x = ![]() . Atunci:
. Atunci:
i) x I N;
ii) x I Z - N;
iii) x I Q Z;
iv) x I R Q.
Alege raspunsul corect.
d. Completeaza spatiile punctate astfel incat afirmatiile sa fie adevarate:
A. Orice subsir al unui sir ce are limita are
B. Daca un sir contine doua subsiruri ce au limite diferite, atunci
C. Orice sir monoton si marginit este
8. Alege itemii perechi dintre urmatorii itemi:
a. Daca rezultatul este adevarul incercuieste litera A, in caz contrar, incercuieste litera F.
xn - l = (x - 1)(xn-1 + xn-2 + . + x + 1) A F
b. Inscrie in spatiul din fata fiecarui numar din
coloana I, litera din coloana II
care indica formula corecta:
I II
1) Aria dreptunghiului A. 2(L + l)
2) Perimetrul dreptunghiului B. (a + b) / 2
3) Media aritmetica a doua numere C. ![]()
4) Media proportionala a doua numere D. L l
c. Se considera numarul real x = ![]() . Atunci:
. Atunci:
i) x I N;
ii) x I Z - N;
iii) x I Q Z;
iv) x I R Q.
Alege raspunsul corect.
d. Completeaza spatiile punctate astfel incat afirmatiile sa fie adevarate:
A. Orice subsir al unui sir ce are limita are
B. Daca un sir contine doua subsiruri ce au limite diferite, atunci
C. Orice sir monoton si marginit este
9. Gaseste itemii cu alegeri multiple dintre urmatorii itemi:
a. Daca rezultatul este adevarul incercuieste litera A, in caz contrar, incercuieste litera F.
xn - l = (x - 1)(xn-1 + xn-2 + . + x + 1) A F
b. Inscrie in spatiul din fata fiecarui numar din
coloana I, litera din coloana II
care indica formula corecta:
I II
1) Aria dreptunghiului A. 2(L + l)
2) Perimetrul dreptunghiului B. (a + b) / 2
3) Media aritmetica a doua numere C. ![]()
4) Media proportionala a doua numere D. L l
c. Se considera numarul real x = ![]() . Atunci:
. Atunci:
i) x I N;
ii) x I Z - N;
iii) x I Q Z;
iv) x I R Q.
Alege raspunsul corect.
d. Completeaza spatiile punctate astfel incat afirmatiile sa fie adevarate:
A. Orice subsir al unui sir ce are limita are
B. Daca un sir contine doua subsiruri ce au limite diferite, atunci
C. Orice sir monoton si marginit este
10. Alege itemii cu raspuns scurt de completare dintre urmatorii itemi:
a. Daca rezultatul este adevarat, incercuieste litera A, in caz contrar, incercuieste litera F.
xn - l = (x - 1)(xn-1 + xn-2 + . + x + 1) A F
b. Inscrie in spatiul din fata fiecarui numar din
coloana I, litera din coloana II
care indica formula corecta:
I II
1) Aria dreptunghiului A. 2(L + l)
2) Perimetrul dreptunghiului B. (a + b) / 2
3) Media aritmetica a doua numere C. ![]()
4) Media proportionala a doua numere D. L l
c. Se considera numarul real x = ![]() . Atunci:
. Atunci:
i) x I N;
ii) x I Z - N;
iii) x I Q Z;
iv) x I R Q.
Alege raspunsul corect.
d. Completeaza spatiile punctate astfel incat afirmatiile sa fie adevarate:
A. Orice subsir al unui sir ce are limita are
B. Daca un sir contine doua subsiruri ce au limite diferite, atunci
C. Orice sir monoton si marginit este
Raspunsuri: l. a; 2. a, 3. b, 4. c, 5. a, 6. b, 7. a, 8. b, 9. c, 10. d.
1. a) Sa se arate ca daca x este un numar real astfel incat x16 si x9 sunt numere rationale, atunci x este numar rational.
b) Sa se arate ca ![]() Z, a, b I Z, b 2.
Z, a, b I Z, b 2.
2. Fie x ![]()
![]() +
+ ![]()
![]() + +
+ + ![]() -
- ![]() si
si
y 1 - ![]() +
+ ![]() -
- ![]() + +
+ + ![]()
![]() .
.
a) Calculati media aritmetica a numerelor x si y.
b) Demonstrati ca x < ![]() < y.
< y.
3. In triunghiul ABC se considera bisectoarea BE, unde E I (AC), un punct P I I (BE) si punctul N astfel incat CP AB . Sa se arate ca daca:
![]() 2
2 ![]() 1, atunci triunghiul ABC
este isoscel.
1, atunci triunghiul ABC
este isoscel.
4. Pe latura [AC]
a triunghiului echilateral ABC se iau
punctele E si F astfel incat AE EF FC ![]() si punctul D pe latura [BC] astfel incat BD CD. Sa se arate ca m( BED) + m( BFD) < 60
si punctul D pe latura [BC] astfel incat BD CD. Sa se arate ca m( BED) + m( BFD) < 60
Solutii si barem de corectare:
1. a) Daca x = 0, afirmatia este evident adevarata. (1p)
Daca x 0, x16 I Q T x80 I Q; x9 I Q T x81 I Q. Deci x = x81 : x80 I Q. (3p)
b) b3 b b(b 1)(b + 1) 3 (1p)
a2 + 1 3, pentru orice a I Z (3p)
Finalizare (1p)
Total 10p
2.
a) ![]()
![]() (2p)
(2p)
b) x ![]() +
+ ![]() + . +
+ . + ![]() (1001 termeni);
(1001 termeni);
y ![]() +
+ ![]() + . +
+ . + ![]() (1001 termeni).
(1001 termeni).
Din ![]() <
< ![]() ,
, ![]() <
< ![]() , .,
, ., ![]() <
< ![]() rezulta x < y. (5p)
rezulta x < y. (5p)
Demonstratia
x < ![]() < y (2p)
< y (2p)
(1p din oficiu)
Total 10 p
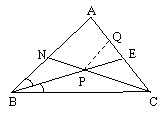 3. Ducem
PQ AN.
Aplicam teorema lui Thales in DACN
si DAEB.
Relatia data
este echivalenta cu:
3. Ducem
PQ AN.
Aplicam teorema lui Thales in DACN
si DAEB.
Relatia data
este echivalenta cu: ![]() -
- ![]() 1 CQ
2EQ = QA CE =
AE T BE mediana si
bisectoare in DABC T [AB]
s [BC]
1 CQ
2EQ = QA CE =
AE T BE mediana si
bisectoare in DABC T [AB]
s [BC]
Total 10p
Observatie: Se poate utiliza teorema lui Menelaus.
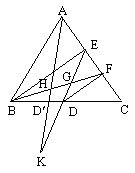 4. Fie D I [BC]
astfel incat BD
4. Fie D I [BC]
astfel incat BD ![]() si = AD BF,
si = AD BF,
BF ED; DBHD A DBFC T BD H s BFC T
T m( BHD m( C 60 (5p)
DF BE T m( EBF s m( BFD) si
m( BGD m( BED) + m( BFD
Dar m( BHK m( BGD) + m( K) = 60 T
m( BED) + m( BFD) < 60 (4p)
(1p din oficiu)
Total 10p
Observatie: Aplicand teorema cosinusului, putem arata ca GE > EF, GF > EF T in DGEF, EF este latura cea mai mica T m( EGF) < 60
1. Daca A si B , demonstrati ca A B
2. a) Aratati ca 3(a2 + b2 + c2) (a + b + c)2, pentru a, b, c I R.
b) Fie a, b, c > 0 numere reale cu a b c 1. Sa se arate ca:
![]() +
+ ![]() +
+ ![]() a + b + c + 3.
a + b + c + 3.
3. Fie ABCD si ABEF romburi situate in plane perpendiculare. Daca m( BAD
= m( FAB 60 aflati:
a) distanta dintre dreptele AB si FD in functie de a AB
b) distanta dintre dreptele FD si BE.
4. Un heptagon inscriptibil are trei unghiuri de masura 120 . Sa se arate ca heptagonul are doua laturi egale.
Solutii si barem de corectare:
1.
Fie x I A
B T x
I A si x I B. Din x I A T ![]() p
I Z T x
p
I Z T x
![]() (3p)
(3p)
Deoarece x I B,
rezulta ![]() I Z
T p 1.
I Z
T p 1.
Deci x ![]()
![]() I A
B si astfel A B (6p)
I A
B si astfel A B (6p)
(1p din oficiu)
Total 10p
2. a) (a b)2 + (b c)2 + (c a)2 0, a, b, c I R. (3p)
b) Inegalitatea este echivalenta cu: ![]() +
+ ![]() +
+ ![]()
2(a + b + c) + 3. Din a2 + b2 + c2
![]() T (a2
+ b2 + c2)
T (a2
+ b2 + c2) ![]()
![]() (a +
b + c)
(a +
b + c) ![]()
![]() 9 3(a
+ b + c). Din a b c
1 T
9 3(a
+ b + c). Din a b c
1 T
T a + b + c 3. Rezulta (a2 + b2
+ c2)![]() 2(a + b + c) + (a + b + c)
2(a + b + c) + (a + b + c)
2(a + b + c) + 3. (6p)
(1p din oficiu)
Total 10p
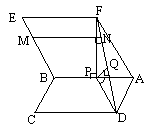 3. a) Fie FP
BA si DP AB T AP
AF cos 60 si
3. a) Fie FP
BA si DP AB T AP
AF cos 60 si
AP AD cos 60 T AP AP T P P T BP (FPD).
Construim PQ FD care este distanta dintre AB si FD T
T PQ ![]() . (4p)
. (4p)
b) (BEC) (FAD); Fie MN BE, M I BE, MN FD, N I FD T
T MN (AFD) T MN distanta dintre planele (BEC) si (FAD);
 MN = d(E,
(FAD)). Notam cu h inaltimea din E in tetraedrul EFAD si se determina cu ajutorul volumului tetraedrului: h SFAD
SEFA DP T h
MN = d(E,
(FAD)). Notam cu h inaltimea din E in tetraedrul EFAD si se determina cu ajutorul volumului tetraedrului: h SFAD
SEFA DP T h
![]() . (5p)
. (5p)
(1p din oficiu)
Total 10p
![]()
![]()
![]()
![]() 4. Presupunem
ca dintre cele trei unghiuri de
120 nu
exista doua alaturate. Fie m( A1 m( A3 m( A5 120 T m( A1A2) +
4. Presupunem
ca dintre cele trei unghiuri de
120 nu
exista doua alaturate. Fie m( A1 m( A3 m( A5 120 T m( A1A2) +
+ m( A1A7 120 ; m( A2A3) + m( A3A4 120 T
![]()
![]()
![]() T m( A6A7 360 3 120 0 ; m( A4A5) + m( A5A6
T m( A6A7 360 3 120 0 ; m( A4A5) + m( A5A6
= 120 ,
contradictie. Deci putem alege m( A1 m( A2
![]()
![]() = 120 T m( A1A7 m( A2A3 T [A1A7] [A2A3]. (9p)
= 120 T m( A1A7 m( A2A3 T [A1A7] [A2A3]. (9p)
(1p din oficiu)
Total 10p
1. a) Sa se determine partea
intreaga a numarului 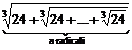 , unde n I N*.
, unde n I N*.
b) Fie x, y
I R astfel incat
x2 + y2 I Q, x3
+ y3 I Q, x4 + y4 I Q. Atunci
x + y I Q si x y I Q.
2. Sa se determine functia f : R
R pentru care f (x)
= x2, x I [0, 1) si
f (x + 1) = f (x) + x,
x I R.
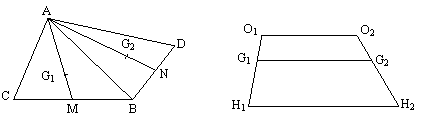
3. Se considera punctele A, B,
C, D coplanare, oricare trei necoplanare si H1, H2
ortocentrele triunghiurilor ABC si
respectiv ABD. Sa se arate
ca A, B, C, D sunt conciclice daca si
numai daca ![]() .
.
4. Fie triunghiul ABC, punctul M I (BC) si cercurile C0 = C (I, r), C1 = C (I1, r1), C2 = C (I2, r2), cercurile inscrise in triunghiurile ABC, ABM respectiv ACM. Sa se arate ca:
a) cercurile C1 si C2, sunt tangente daca si numai daca M I C0;
b) Daca M I C0, atunci exista relatia: p
![]() , unde S, D
sunt mijloacele segmentelor [AM] respectiv [BC], I
I SD,
, unde S, D
sunt mijloacele segmentelor [AM] respectiv [BC], I
I SD, ![]() .
.
Barem de corectare
1. a) xn =![]() , n I N*,
2 < xn < 3, n
1.
Demonstratie prin inductie. Deci [xn] = 2, n
1. (4p)
, n I N*,
2 < xn < 3, n
1.
Demonstratie prin inductie. Deci [xn] = 2, n
1. (4p)
b) Daca a b
= 0. Pentru a = b = 0 totul este evident. Pentru a 0 = b T a2
I Q,
a3 I Q T a
I Q T a
+ b I Q
si a b
I Q. Daca a b 0. Atunci (a2 + b2)(a4 + b4) - (a3
+ b3)2 =
= a2b2(a - b)2 I Q.
Dar (a2 + b2)2
- (a4 + b4) = 22b2 I Q
T (a - b)2
I Q T a
b I Q
T T a2 - ab + b2 I Q.
Dar a3 + b3 = (a + b)(a2 - ab + b2) I Q
T a + b
I Q. (5p)
(1p din oficiu)
Total 10p
2.
Fie g(x) = f (x)
![]() . Avem g(x + 1) = g(x), x
I R si prin inductie g(x
+ n) =
. Avem g(x + 1) = g(x), x
I R si prin inductie g(x
+ n) =
= g(x), n I Z,
x I R.
Din x = [x] + , rezulta ca g(x) = g(). Cum I [0, 1) T
T f () = . Din f (x) = g(x) +![]() = g() +
= g() + ![]() =
=
 = f ()
= f () ![]() . (9p)
. (9p)
(1p din oficiu)
Total 10p
3.
![]()
=![]() (1)
(1)
![]() ;
; ![]() . Deci
. Deci ![]() .
.
Avem ![]() O1 s O2 A, B, C, D sunt conciclice. (9p)
O1 s O2 A, B, C, D sunt conciclice. (9p)
 (1p din oficiu)
(1p din oficiu)
Total 10 puncte
4. a) V1
si V2 punctele de
tangenta cu dreapta AM ale
cercurilor C1, respectiv C2. Cercurile C1
si C2 sunt tangente AV1
= AV2 ![]()
![]() (AM + b - MC) MB
= p - b, MC = p - c
M I C0. (3p)
(AM + b - MC) MB
= p - b, MC = p - c
M I C0. (3p)
b)
![]() , unde D este piciorul bisectoarei din A;
, unde D este piciorul bisectoarei din A; ![]() T
T
T![]() ;
; ![]() ,
,
![]() T
T![]() , inlocuind
se verifica relatia ceruta
, inlocuind
se verifica relatia ceruta ![]() si
si ![]() . (6 p)
. (6 p)
(1p din oficiu)
Total 10 puncte
1. a) Daca in tetraedrul regulat ABCD au loc conditiile AB CD si AC BD, atunci AD BC.
b) Fie un
patrulater convex ABCD si M mijlocul lui (CD). Daca AB = BC +
+ AD si BM este perpendicular pe AM
sa se arate ca BC si AD sunt paralele.
2. Fie a, b, c, d numere complexe cu acelasi modul astfel incat a + b + c = d. Sa se arate ca unul din numerele a, b, c este egal cu d.
3. a) Fie p, n I N*,
p > 2n. Sa se arate ca: ![]() , unde [x] este partea intreaga a numarului real x.
, unde [x] este partea intreaga a numarului real x.
b) Fie m, n, p I N* si a, b, c I (0, 1) sau a, b, c I (1, + ). Aflati minimul expresiei: E = (loga b)m + (logb c)n + (logc a)p.
4. a) Fie M, N, P, Q varfurile unui patrulater convex. Atunci SMNPQ =
= ![]() MP NQ sin a, unde a este unghiul determinat de diagonalele patrulaterului.
MP NQ sin a, unde a este unghiul determinat de diagonalele patrulaterului.
b) Sa se arate ca in orice triunghi ABC are loc relatia:
![]()
![]() , unde S este aria
triunghiului iar ma, mb,
mc reprezinta lungimile medianelor corespunzatoare
laturilor a, b, c.
, unde S este aria
triunghiului iar ma, mb,
mc reprezinta lungimile medianelor corespunzatoare
laturilor a, b, c.
Barem de corectare
1. a) Fie O originea unui
reper. Atunci AB CD
![]() si AC BD
si AC BD
![]() . Obtinem
. Obtinem ![]() si
si ![]()
![]() . Scazand aceste relatii obtinem
. Scazand aceste relatii obtinem ![]() , adica
, adica ![]() T AD BC. (3p)
T AD BC. (3p)
b) Fie ![]() ,
, ![]() ,
, ![]() , v1 = b, v2 = c, v3 = d.
Avem:
, v1 = b, v2 = c, v3 = d.
Avem:
![]() ,
, ![]() . Din
. Din ![]() T 4v1 v3
+ 2v2 (v1
+ v3) + c2 = 0,
T 4v1 v3
+ 2v2 (v1
+ v3) + c2 = 0, ![]() , BA2 =
(b + d)2 = (v1 + v2 + v3)2
= b2 + c2 + d2 + 2v1v2 + 2v1v3
+ 2v2v3. Scazand relatiile obtinute bd = bd cos j T cos j 1 T j p, adica BC AD. (6p
, BA2 =
(b + d)2 = (v1 + v2 + v3)2
= b2 + c2 + d2 + 2v1v2 + 2v1v3
+ 2v2v3. Scazand relatiile obtinute bd = bd cos j T cos j 1 T j p, adica BC AD. (6p
(1p din oficiu)
2. Solutia I. Putem presupune, fara a restrange
generalitatea, ca numerele a, b, c,
d au modulul 1 (daca au modulul r > 0, le impartim prin r si obtinem numere de modul
1, iar daca
r = 0, problema este banala).
Trecand la conjugate in egalitate: a
+ b + c = d, obtinem ![]() sau d(ab
+ bc + ca) = abc. Calculam
produsul (d - a)(d - b)(d
- c) si avem: (d -
a)(d - b)(d - c) = d3
(a + b
+ c)d2 + (ab + bc + ca)d abc
= 0. Rezulta a = d sau b =
sau d(ab
+ bc + ca) = abc. Calculam
produsul (d - a)(d - b)(d
- c) si avem: (d -
a)(d - b)(d - c) = d3
(a + b
+ c)d2 + (ab + bc + ca)d abc
= 0. Rezulta a = d sau b =
= d sau c = d. (1p
(1p din oficiu)
Solutia II. In planul complex fie A(a),
B(b),
C(c),
D(d)
pe un cerc cu centrul in origine. Ortocentrul H al triunghiului ABC are
afixul a + b + c (Sylvester),
adica H(d), deci
H = D. Deci DABC este dreptunghic si D = A sau D = B
sau D = C.
3. a) ![]() , 0 k n (inegalitatea Bernoulli) si insumand obtinem
, 0 k n (inegalitatea Bernoulli) si insumand obtinem
n + 1 <![]() . Rezulta concluzia. (4p)
. Rezulta concluzia. (4p)
b) loga b, logb c, logc a I (0, ) si produsul P = loga b logb
c logc
a = 1. Minimul expresiei E are loc
cand ![]() T 1 = k3 m
n p
T
T 1 = k3 m
n p
T![]() .
.
Deci Emin =![]() . (5p
. (5p
(1p din oficiu)
 4. a)
Se utilizeaza formula ariei unui triunghi S =
4. a)
Se utilizeaza formula ariei unui triunghi S =![]() . (2p)
. (2p)
b) SBCDE =![]() T mb mc
=
T mb mc
= ![]() .
.
Deci ![]() si
si
a b g p. Rezulta ca ![]() . (7p
. (7p
(1p din oficiu)
Total 10p
1. a) Fie A o matrice patrata de ordin 4 cu elemente intregi. Daca elementele diagonalei principale au aceeasi paritate, diferita de paritatea celorlalte 12 elemente, atunci det (A) 0.
b) Fie (an)n 1, un sir de numere reale strict pozitive care satisfac relatia:
(an+1
an)2 = an, n
I N*. Sa se calculeze L =![]() , stiind ca aceasta limita exista.
, stiind ca aceasta limita exista.
2. a) Fie A I M3(R), A
= 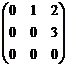 . Sa se determine matricele X I M3(R) pentru care A X = X A.
. Sa se determine matricele X I M3(R) pentru care A X = X A.
b) Sa se rezolve ecuatia Xn = A, cu X I M3(R) si n I N*.
3. a) Se considera sirul an =![]() , n I N*.
Sa se arate ca
, n I N*.
Sa se arate ca ![]() si
si ![]() .
.
b) Fie ABCD un dreptunghi de dimensiuni a, b iar r > 0. Definim M(r) multimea
punctelor din planul dreptunghiului situate la distanta r
fata de figura ABCD. Notand
cu A(r) aria multimii plane M(r), sa se calculeze ![]() .
.
4. Fie a I R si f : R R o
functie pentru care f (x) f (y) + f
(x) + f (y) =
= f (xy) + a, x, y I R.
a) Sa se determine a I R stiind ca functia f este bijectiva. In acest caz sa se calculeze f ( 1), f (0) si f (1).
b) Sa se determine functiile continue ce verifica punctul a).
Barem de corectare
1. a) Daca elementele diagonalei principale sunt impare atunci A = I4 (mod 2), deci det (A) este impar T det (A) 0. Daca elementele diagonalei principale sunt pare, atunci A2 are elementele diagonalei principale impare T det (A2) 0 T det (A) 0. (3p)
b) Daca sirul ar fi divergent T L
= + (deoarece an > 0, n
I N*). Daca sirul
este convergent, atunci L I R.
Trecand la limita in relatia de recurenta obtinem L = 0. Deci n0
I I N*
astfel incat n n0
avem 0 < an < 1. Dar
an+1 an
= ![]() . Cum 0 < an <
. Cum 0 < an <![]() ,
,
n n0,
nu putem avea an+1
= an ![]() < 0, deci an+1
= an +
< 0, deci an+1
= an +![]() > an,
n n0, deci (an)n nu poate converge la 0.
Prin urmare L = + (6p
> an,
n n0, deci (an)n nu poate converge la 0.
Prin urmare L = + (6p
(1p din oficiu)
2. a) Fie X
=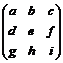 . Din AX = X A
rezulta X =
. Din AX = X A
rezulta X =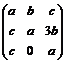 , a, b, c I R. (3p)
, a, b, c I R. (3p)
b)
Din Xn = A T Xn
+ 1 = AX = X A,
deci X =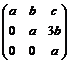 .
.
Avem det (Xn) =
det (A) = 0 T det (X)
= 0 = a3 T a
= 0 T X =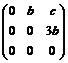 . Rezulta
. Rezulta
X2 =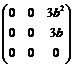 si Xn
= O3, n 3. Pentru a avea Xn = A,
singura posibilitate este n = 1
si X = A. (6p)
si Xn
= O3, n 3. Pentru a avea Xn = A,
singura posibilitate este n = 1
si X = A. (6p)
(1p din oficiu)
3. a) ![]() .
.
Asadar an = ![]() , adica an =
, adica an =![]() , n I N*
si
, n I N*
si ![]() .
.
bn =![]() , unde un=
, unde un=![]() si
si
vn =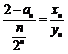 , unde xn
= 2 an 0 si yn =
, unde xn
= 2 an 0 si yn =![]() 0. Aplicam lema Stolz (caz
0. Aplicam lema Stolz (caz ![]() ):
): 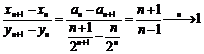 . Deci vn
=
. Deci vn
=![]() si bn
un vn
si bn
un vn
![]() .
.
(3p)
(1p din oficiu)
4. a) Pentru x = y
avem [f (x) + 1]2 = f (x2) + a + 1. Cum f este surjectiva, x0 I R
astfel incat f (x0) = 1. Deci ![]() = a 1. Pentru x = -x0 avem
= a 1. Pentru x = -x0 avem ![]() + a + 1 = 0 T f ( x0 1, deci x0
= 0 si f (0) = 1, de unde obtinem a = 0. Deci f 2(x) = f (x2)
2f (x).
Pentru x = 1,
+ a + 1 = 0 T f ( x0 1, deci x0
= 0 si f (0) = 1, de unde obtinem a = 0. Deci f 2(x) = f (x2)
2f (x).
Pentru x = 1,
f 2(1) = f (1). Cum f (1) -1 rezulta f (1) = 0.
Pentru x = 1, f 2 1) = f (1) 2f ( 1) T T f 2( 1) = 2f ( 1) si cum f ( 1) 0 T f ( 1) = 2. (3p
b) Functia g(x) = f
(x) + 1 este continua,
verificand ecuatia de tip Cauchy,
g(x)
g(y)
= g(x y), x,
y I R,
cu g(0) = 0 si g(1) = 1 si are solutia g(x)
= xa pentru x
> 0. Deci g(x) = 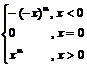 , de unde f (x) =
, de unde f (x) = 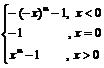 . (6p)
. (6p)
(1p din oficiu)
1. Fie (G, ) un grup si H o submultime a lui G nevida si diferita de G avand proprietatea: x I H, y I G H T xy I G H. Sa se demonstreze ca H este un subgrup al lui G.
2. Sa se calculeze ![]() , x I (0, +
, x I (0, +
3. Fie f : [0, 1] R. f(x) = (x2 + 1)ex. Sa se calculeze:
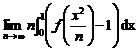 .
.
4. Fie A = . Sa se arate ca:
a) A este subinel al lui Q[X];
b) Z[X] nu este izomorf cu A.
Barem de corectare
1. e I H (2p): Prin absurd e I G H; fie x I H, rezulta xe I G H, rezulta x I G H, contradictie.
x I H T x 1 I H (3p): Prin absurd daca exista x I H astfel incat x 1 I G H, rezulta xx 1 I G H, rezulta e I G H, contradictie.
x, y I H T xy I H (4p): Prin absurd daca exista x, y I H astfel incat x, y I G H. Cum x 1 I H rezulta ca x 1(xy) I G H, rezulta y I G H, contradictie.
2. ![]() ln x + C =
ln x + C =
=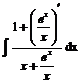 ln x + C =
ln x + C =![]() + C. (9p)
+ C. (9p)
3. ![]() . Cum
. Cum ![]() , rezulta
, rezulta ![]() . Avem
. Avem ![]() pentru orice x I [0, 1]. Prin urmare, rezulta:
pentru orice x I [0, 1]. Prin urmare, rezulta: ![]() . Trecand la limita, conform principiului clestelui
avem
. Trecand la limita, conform principiului clestelui
avem ![]() . Asadar, sirul considerat este convergent si
limita sa este
. Asadar, sirul considerat este convergent si
limita sa este ![]() . (2p)
. (2p)
4. a) Fie f g I A si n I Z: (f + g)(n) = f (n) + g(n) I Z T f + g I A, (f g)(n) = f (n) g(n) I Z T f g I A, f = 1 I Z T 1 I A. (3p)
b) Presupunem ca inelele A si Z[X] sunt izomorfe. Deci j : Z[X] A un izomorfism de inele (j(1) = 1). Deoarece j este surjectiva T j este un polinom de gradul 1, j(X) = aX + b, a, b I Q, n 0. (2p)
Fie gk+1(X) =![]() I Q[X]: daca t I Z,
I Q[X]: daca t I Z, ![]() I Z, deoarece produsul a(k 1) numere intregi
consecutive se divide cu (k + 1)!.
Deci gk 1 I A. Cum j este surjectiva T fk 1 I Z[X] astfel incat j(fk 1) = gk 1: fk+1
= ak+1Xk+1 + ak Xk + . + a1 X + a0
I Z, deoarece produsul a(k 1) numere intregi
consecutive se divide cu (k + 1)!.
Deci gk 1 I A. Cum j este surjectiva T fk 1 I Z[X] astfel incat j(fk 1) = gk 1: fk+1
= ak+1Xk+1 + ak Xk + . + a1 X + a0
ak+1(aX + b)k+1 + ak(aX + b)k + . + a1(aX + b) + a0
= gk 1(X) T ak 1 ak 1 = ![]() . Scriem a =
. Scriem a = ![]() , (u, v) = 1: deci ak+1 uk 1 (k
+ 1)! = vk 1, egalitatea imposibila pentru orice
, (u, v) = 1: deci ak+1 uk 1 (k
+ 1)! = vk 1, egalitatea imposibila pentru orice
k I N
(u, v) sunt fixate si putem considera k suficient de mare astfel incat (k + 1)! sa contina un numar prin p ce nu apare
in descompunerea lui v in factori
primi). Deci Z[X] nu este izomorf cu A.
V.146 din nr. 3-4/2002
Aflati restul impartirii numarului a = 1 2 3 19 + 2002 la numarul 20.
Solutie: a = 1 2 3 4 5 19 + 20 100 + 2 = 20(1 2 3 6 19 + 100) + 2. Deci r = 2 (restul impartirii).
V.3 din nr. 5-6/2002
Adunarea DVII + DVII = MXIV este adevarata considerand numerele scrise cu cifre romane. Sa se inlocuiasca literele cu cifre astfel incat adunarea sa ramana corecta.
Solutie. Trebuie sa avem I 0 (astfel ar rezulta V = 0). Pentru a obtine I la cifra zecilor din MXIV, ramane doar posibilitatea I = 9 si rezulta V = 8. Adunarea devine:
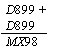
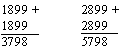 Analizand valorile posibile pentru D (care nu poate fi mai mare decat 4),
obtinem solutiile:
Analizand valorile posibile pentru D (care nu poate fi mai mare decat 4),
obtinem solutiile:
V.155 din nr. 7-8/2002
Un elev a rezolvat ![]() dintr-un numar de probleme. Daca ar mai fi
rezolvat inca 3 probleme atunci numarul problemelor rezolvate ar fi
de 5 ori mai mare decat al celor nerezolvate. Cate probleme si-a propus
sa rezolve.
dintr-un numar de probleme. Daca ar mai fi
rezolvat inca 3 probleme atunci numarul problemelor rezolvate ar fi
de 5 ori mai mare decat al celor nerezolvate. Cate probleme si-a propus
sa rezolve.
Solutie.
Notam cu x numarul de
probleme propuse. Observam ca numarul problemelor nerezolvate
reprezinta ![]() . Deci putem scrie:
. Deci putem scrie: ![]() x = 90.
x = 90.
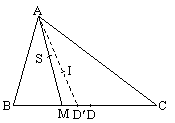
V.140 din nr. 7-9/2002
In triunghiul ABC, bisectoarea C intersecteaza pe (AB) in D si pe inaltimea din A pe BC in E, E I (CD). Daca (AE) s (AD) sa se afle m( BAC
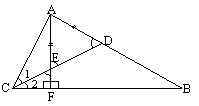 Solutie: Din (AE) s (AD) T DAED este isoscel T m( (AED))
= m ( (ADE)), dar (AED)
s (CEF)
opuse la varf. Avem: m( CEF) + m( C1) = 90 T m( ADE) + m( C2) = 90 (C1
s C2 din ipoteza) T m( CAB) = 90
Solutie: Din (AE) s (AD) T DAED este isoscel T m( (AED))
= m ( (ADE)), dar (AED)
s (CEF)
opuse la varf. Avem: m( CEF) + m( C1) = 90 T m( ADE) + m( C2) = 90 (C1
s C2 din ipoteza) T m( CAB) = 90
VII.161 din nr. 9-10/2002
Fie M un punct in interiorul unui patrat ABCD. Atunci segmentele MA, MB, MC, MD sunt laturile unui patrulater convex.
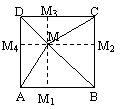 prof. Marian Dinca
prof. Marian DincaSolutie. Fie patratul ABCD si M I Int ABCD, fie M1, M2, M3, M4 proiectiile lui M pe laturile patratului. Atunci MM1BM2; MM2CM3; MM3DM4; MM4AM1 sunt dreptunghiuri deci au diagonalele egale. Rezulta ca MA = M1M4, MB = M1M2, MC = M3M2, MD = M3M4.
Deci segmentele MA, MB, MC, MD sunt egale cu laturile patrulaterului M1M2M3M4.
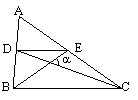
VII.163 din nr. 9-10/2002
Fie ABC
un triunghi echilateral si P un
punct in interiorul sau. Se noteaza: =
= (AP (BC),
= (BP
(AC), = (CP (AB).
Sa se arate ca, daca AA = BB = CC , atunci P coincide cu centrul de simetrie
al triunghiului ABC.
Solutie.
Se noteaza ![]() ,
, ![]() ,
, ![]() (deoarece din teorema
lui Ceva, AA , BB si CC fiind concurente in P, avem
(deoarece din teorema
lui Ceva, AA , BB si CC fiind concurente in P, avem ![]() 1, k1
> 0, k2 > 0, k3 > 0).
1, k1
> 0, k2 > 0, k3 > 0).
Folosind relatia lui Stewart, in
conditiile de mai sus, si considerand lungimea laturii triunghiului
ABC egala cu a avem: AA 2 = a2 ![]() , BB 2 = a2
, BB 2 = a2 ![]() , CC 2 = a2
, CC 2 = a2 ![]() . Din AA 2 = BB 2 = CC 2 T
. Din AA 2 = BB 2 = CC 2 T ![]() T
T![]() T
T
T I. 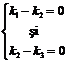 sau II.
sau II. 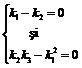 sau III.
sau III. 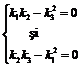 sau
sau
IV. 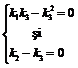 . Din variantele I, II, III rezulta imediat k1 = k2 = k3
(1).
. Din variantele I, II, III rezulta imediat k1 = k2 = k3
(1).
Din IV T k3 =![]() T k1k2 =
T k1k2 =![]()
![]() T k1 = k2 T k3
= k1, deci k1 = k2 = k3
(2).
T k1 = k2 T k3
= k1, deci k1 = k2 = k3
(2).
> 0 > 0
Din(1) si (2) rezulta ca in toate variantele, k1 = k2 = k3 T A , B si C sunt mijloacele laturilor T P s G (centru de greutate al triunghiului ABC) q.c.d.
VII.164 din nr. 9-10/2002
In triunghiul ABC, m (A) = 60 , ![]() , BC =
, BC =![]() cm. Sa se calculeze perimetrul si aria
triunghiului ABC.
cm. Sa se calculeze perimetrul si aria
triunghiului ABC.
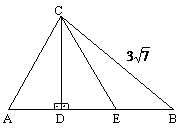 Solutie: Notam
Solutie: Notam ![]() TAB = 3a, AC = 2a.
TAB = 3a, AC = 2a.
Avem: AD = DE = EB = a, DACE = echilateral cu
AC
= AE = CE = 2a, CD AB
T CD =![]() .
.
Din DCDB, m( D) = 90 ![]() CD2 + DB2 = BC2 T
CD2 + DB2 = BC2 T
3a2 + 4a2 = 63 a = 3 T AB = 9 cm, AC = 6 cm.
P
=![]() cm, A =
cm, A =![]() cm2.
cm2.
IX.161 din nr. 3-4/2002
Sa se calculeze suma Sn =![]() , n I N*
si sa se demonstreze rezultatul gasit prin inductie
matematica.
, n I N*
si sa se demonstreze rezultatul gasit prin inductie
matematica.
Solutie: Sn ![]()
![]()
![]()
![]()
= 1(15 -1 + 1) + 2(80 - 16 + 1) + + k[(k + 1)4 - 1 - k4
+ 1] + + (n - 1)[n4 - 1 - (n - 1)4 + 1] =
= 1(24 - 1) + 2(34 - 24) + + k[(k + 1)4
- k4 ] + + (n - 1)[n4 -(n - 1)4] =
= ![]() +
+ ![]() +
+
![]() .
.
IX.3 din nr. 5-6/2002
Rezolvati ecuatia:![]() .
.
Solutie. Notez ![]() , x 0 si a 0.
, x 0 si a 0.
![]()
![]()
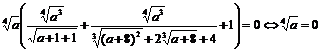 .
.
Deci: a
= 0 ![]() . Cum [
. Cum [![]() ] I Z si
] I Z si ![]() I [0, 1) T 3
I [0, 1) T 3![]() I [0, 3) Z =
I [0, 3) Z =
= T
1)
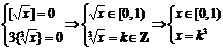 T x = 0;
T x = 0;
2)
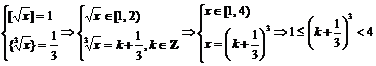 T
T
T1 k
+![]() .
.
3)
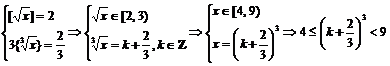 T
T
T![]() , S =
, S =![]() .
.
IX.167 din nr. 7-8/2002
Rezolvati in R ecuatia: ![]() . ([x] = partea
intreaga a numarului real x.)
. ([x] = partea
intreaga a numarului real x.)
Solutie: [x] >
0 T [x] 1 T x
I [1, ). Tinand cont de faptul ca [x + k] =
= [x] + k, k I Z
si notand [x] = y = 0, y > 1, y I Z
avem:
![]() . Insa:
. Insa: ![]() .
.
Analog
![]() .
.
Deci ![]() =
=
=![]() . Prin urmare pentru a avea egalitate T y
= 1 T [x] = 1 T x
I [1, 2).
. Prin urmare pentru a avea egalitate T y
= 1 T [x] = 1 T x
I [1, 2).
Observatie. Problema poate fi generalizata astfel: Rezolvati in R ecuatia:
![]() si solutia
este asemanatoare.
si solutia
este asemanatoare.
IX.173 din nr. 9-10/2002
Sa se determine f : R R injectiva, cu proprietatea ca:
f (x + f (y + f (z))) = f (x + y + z + 1) + 1, x, y, z I R.
Solutie. Pentru y = z = 0 obtinem: f (x + f (f (0))) = f (x + 1) +1, x I R. (1)
Notam f (0) = a. Atunci: f (x + f (a)) = f (x + 1) + 1. (1
Pentru y = z: avem f (x + f ( z + f (z))) = f (x + 1) + 1, x I R. (2)
De aici (din (1) si (2) deducem: f (x + f ( z + f (z))) = f (x + f (a)), x, z I R. (3)
Dar f este injectiva. Din (3) rezulta: x + f ( z + f (z)) = x + f (a) T f ( z + f (z)) = f (a). (4)
Aplicam din nou injectivitatea T f (z) - z = a T f (z) = z + a. (5)
Tinem cont de (5) in relatia din enunt. Atunci:
f (x + f (y + f (z))) = x + f (y + f (z)) + a = x + y + f (z) + 2a = x + y + z + 3a.
Apoi: f (x + y + z + 1) + 1 = x + y + z + 2 + a. De unde: 2a = 2, a = 1. Asadar, functia cautata este: f (x) = x + 1.
XI.174 din nr. 9-10/2002
Sa se arate ca oricare ar fi numarul radicalilor, avem inegalitatea
![]() .
.
Solutie. Fie xn
=![]() , unde numarul radicalilor este n, n I N*. Este
evident ca: xn <
, unde numarul radicalilor este n, n I N*. Este
evident ca: xn <![]() = yn,
unde numarul radicalilor este n.
Deci, xn < yn = yn 1 = = y2
=
= yn,
unde numarul radicalilor este n.
Deci, xn < yn = yn 1 = = y2
=![]() .
.
IX.175 din nr. 9-10/2002
Rezolvati ecuatia ![]() .
.
Solutie. Din conditiile de existenta a radicalilor, avem
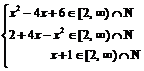 echivalent cu
echivalent cu 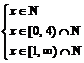 , adica x I
, adica x I
Verifica
ecuatia doar x = 3, conform ![]() .
.
X.1 din nr. 5-6/2002
Fie (un)n 1 o progresie aritmetica de ratie r > 0, cu u1 > 0. Daca (xn)n 0 este un sir de numere reale strict pozitive astfel incat xn + 2 = xn + 1 xn n I N, atunci:
![]() , n I N*.
, n I N*.
Solutie. Demonstram cerinta ecuatiei prin metoda inductiei matematice.
n
= 1 T![]() x1 x2
= x3 ceea ce arata
ca pentru
x1 x2
= x3 ceea ce arata
ca pentru
n = 1 enuntul este
adevarat.
Presupunem enuntul adevarat pentru n si sa-l demonstram si pentru n + 1, adica:
![]() =
= ![]()
![]() =
=![]()
![]()
![]() ceea ce arata ca ecuatia este
adevarata si pentru n
+ 1. Conform principiului inductiei matematice rezulta ca
enuntul este adevarat pentru orice n I N*.
ceea ce arata ca ecuatia este
adevarata si pentru n
+ 1. Conform principiului inductiei matematice rezulta ca
enuntul este adevarat pentru orice n I N*.
X.6 din nr. 5-6/2002
Daca zA, zB, zC sunt afixele varfurilor triunghiului ABC cu zA zB zC = R, atunci (zA + zB)(zB + zC)(zC + zA) R3. Cand are loc egalitatea?
 Solutie. Afixele mijloacelor A1, B1, C1
ale laturilor BC, CA, AB,
sunt respectiv,
Solutie. Afixele mijloacelor A1, B1, C1
ale laturilor BC, CA, AB,
sunt respectiv, ![]() ,
, ![]() ,
, ![]() . Atunci
. Atunci
OA1 =![]() , OB1 =
, OB1 =![]() , OC1 =
, OC1 =![]() .
.
Relatia se scrie zA + zB zB + zC zC + zA R3, adica
2OA1 2OB1 2OC1 R3. (
Dar in triunghiul OA1B dreptunghic in A1,
avem OA1 = R sin a, unde a = m( (OBA1)),
insa 2a + 2b + 2g = 180 , de unde a b g = 90 si a = 90 b g = 90 A.
Atunci OA1 = R sin (90 A)
= R cos A, analog OB1
= R cos B si OC1
=
= R cos C. Relatia ( ) devine R cos A R
cos B R
cos C ![]() , de unde
, de unde
cos A
cos B cos C ![]() , adevarata in orice triunghi ABC.
, adevarata in orice triunghi ABC.
X.174 din nr. 9-10/2002
Rezolvati ecuatia 40x + 273x + 303x = 364x.
Solutie: x = 3 solutie: 403
+ 2733 + 3033 = 3643. Vom demonstra ca
este unica: impartind cu 364x
ecuatia devine: ![]() .
.
Notam f : R R,
f(x)
=![]() strict descrescatoare, ca suma de functii
strict descrescatoare.
strict descrescatoare, ca suma de functii
strict descrescatoare.
Daca x < 3 T f (x) > f (3) = 1, adica ecuatia nu are radacini mai mici ca 3.
Daca x > 3 T f (x) < f (3) = 1, adica ecuatia nu are radacini mai mari ca 3.
Ramane x = 3 unica.
XI.141 din nr. 1-2/2002
Sa se arate ca functia f : R R, f (x) = arctg x nu este polinomiala.
Solutie. Prin reducere la absurd:
presupunem f polinomiala. Atunci
exista n I N*
astfel incat f (n)(x) = 0, x I R.
Dar f (x)
=![]() , iar
, iar ![]() , i2 = 1.
, i2 = 1.
f (x)
=![]() ;
;
f (x)
=![]() =
=![]() ;
;
Conchidem
f (n)(x) =![]() =
=
=![]() inductie. Dar
inductie. Dar ![]() , apoi
, apoi
x + i
=![]() , ctg t = x T t
= arcctg x sau t = arctg
, ctg t = x T t
= arcctg x sau t = arctg![]() . Rezulta
. Rezulta
![]() .
.
Analog ![]() . Atunci
. Atunci
![]() .
.
Deci
f (n)(x) =![]() , adica
, adica
f (n)(x)
=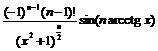 sau f (n)(x) =
sau f (n)(x) =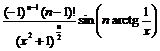 oricare
oricare
x I R*,
n I N*.
Urmeaza ca ![]() oricare x > 0 de exemplu, ceea ce este
absurd! Deci presupunerea este falsa si f nu este functie polinomiala.
oricare x > 0 de exemplu, ceea ce este
absurd! Deci presupunerea este falsa si f nu este functie polinomiala.
XI.160 din nr. 9-10/2002
Fie a, b I![]() astfel incat b
> a si (an)n
1 un sir de numere strict pozitive cu proprietatea ca
astfel incat b
> a si (an)n
1 un sir de numere strict pozitive cu proprietatea ca ![]() . Sa se studieze convergenta sirului bn =
. Sa se studieze convergenta sirului bn =![]() , p I R
fixat.
, p I R
fixat.
Grabriel Dospinescu
Solutie. Fie cn =![]() , n 1. Deducem ca an + 1
, n 1. Deducem ca an + 1 ![]() T
T
T an+1
(n!)b
a an((n - 1)!)b a
= na(n!)b
acn T ![]() =
=
=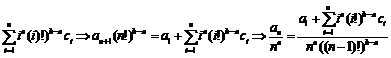 (1).
(1).
Sirul xn = na((n 1)!)b a e crescator, nemarginit, deci putem aplica teorema Cesaro-Stolz. Din (1) deducem ca:
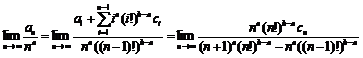 =
=
=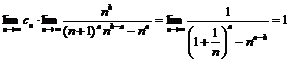 . Deci
. Deci ![]() , p I R
T
, p I R
T![]() . Deducem ca seriile
. Deducem ca seriile ![]() si
si ![]() au aceeasi natura. Dar seria
au aceeasi natura. Dar seria ![]() este convergenta
pentru ap > 1 T p
<
este convergenta
pentru ap > 1 T p
<![]() si divergenta pentru p
si divergenta pentru p ![]() . Deci: daca p <
. Deci: daca p <![]() , bn e
convergent;
, bn e
convergent;
daca p ![]() , bn e
divergent.
, bn e
divergent.
XII.119 din nr. 3-4/2002
Fie inelul (A, +, ) si x I A cu proprietatea ca exista p I N* astfel incat xp + 1 = xp. Sa se arate ca 1 - x + x2 este ireversibil.
Solutie. Fie y = x - x2. Demonstram ca (x
- x2)p = 0. Avem (x
- x2)p = xp(1
- x)p (pentru ca x
si (1 - x) comuta). Dar xp(1 - x)p = xp(1 - x)(1 - x)p-1 = (xp - xp+1)(1 - x)p 1 = 0 si deci yp = 0. Atunci 1 = 1 - yp = (1 - y)![]() =
=![]() (1 y) adica 1 y
este inversabila. Cum 1 y
= 1 x + x2
rezulta cerinta din enunt.
(1 y) adica 1 y
este inversabila. Cum 1 y
= 1 x + x2
rezulta cerinta din enunt.
XII.120 din nr. 3-4/2002
Fie inelul (A,
+, ) in care 1 0 si cu proprietatea ca
exista un unic element
a I A
astfel incat 1 + a + a2 = 0. Sa se arate
ca:
i) 1 + 1 + 1 = 0
ii) x2002 = 0 x1001 = 0, unde x I A.
Solutie. Fie f (a) = 1 + a + a2.
i) f ( 1 - a) = 1 + ( 1 - a) + ( 1 - a)2 = 1 1 a + 1 + a + a + a2 = 1 + a + a2 = f (a) = 0 si cum a e unic obtinem 1 - a = a adica 1 = a - a 1 = a(1 + 1)(1).
Dar 1 + a + a2 = 0 1 = a - a2 = a(1 + a) = (1 + a)( a) adica (-a) este inversabil si ( a 1 = 1 + a. Inmultind (1) cu ( a 1 obtinem 1 + a = 1 + 1 adica a = 1. Atunci (1) devine 1 = 1 1 si prin urmare 1 + 1 + 1 = 0.
ii)
Daca x1001 = 0
evident, x2002 = 0. Fie x I A
cu x2002 = 0. Avem f (1 + x1001) = 1 + 1 +
+ x1001
+ 1 + x1001 + x1001 + x2002 = 1 + 1 + 1 + x1001(1
+ 1 + 1) + x2002 = 0
(pentru ca 1 + 1 + 1 =
= 0 si x2002 = 0).
Deci f (1 + x1001) = 0 si din unicitatea lui a = 1 obtinem 1 + x1001 = 1, adica x1001 = 0.
O.L.83 din nr. 9-10/2002
Fie n I N*
si
multimea An = ,
unde en =![]() . Sa se afle toate numerele p pentru care exista m
impar si x, y I Ap astfel incat x y,
. Sa se afle toate numerele p pentru care exista m
impar si x, y I Ap astfel incat x y,
![]() , iar
, iar ![]() e
radacina de ordinul m a unitatii.
e
radacina de ordinul m a unitatii.
Solutie. Fie p I N* - pentru
care exista x, y I Ap
cu proprietatea din enunt. Atunci
exista m impar si a, b,
c, d I Q cu a + b 0, c + d
0, x = aep + b, y
= cep + d, unde
ep =![]() . Ipoteza afirma ca
. Ipoteza afirma ca 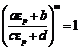 T aep + b cep + d T a2
+ b2 +
T aep + b cep + d T a2
+ b2 +
+ 2ab cos![]() = a2 + b2 c2
d2 (1).
= a2 + b2 c2
d2 (1).
Presupunem
ca ab = cd![]() T (a + b)2 - 2ab = (c + d)2
- 2cd T
T (a + b)2 - 2ab = (c + d)2
- 2cd T 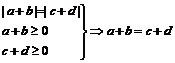 . Fie ab = cd = x,
a + b = c + d = y.
Atunci a, b si c, d sunt radacini ale
ecuatiei t2 yt
+ x = 0, adica
= . Daca a = c T b
= d T x
= y, contradictie!
. Fie ab = cd = x,
a + b = c + d = y.
Atunci a, b si c, d sunt radacini ale
ecuatiei t2 yt
+ x = 0, adica
= . Daca a = c T b
= d T x
= y, contradictie!
Daca a = d
T b = c
T y = bep + a
=![]() =
=![]() =
=
= ![]() , contradictie! Deci ab
cd
, contradictie! Deci ab
cd![]() I Q. Numim intreg algebric
un numar complex z pentru care
exista n, a1, , an-1
I Z astfel incat.
I Q. Numim intreg algebric
un numar complex z pentru care
exista n, a1, , an-1
I Z astfel incat.
zn + a1zn - 1 + + an - 1 = 0. Se arata imediat ca daca un intreg algebric e rational atunci e intreg si ca suma a 2 intregi algebrici e intreg algebric.
Cum
ep = 1 T ep - 1 = 0 T e intreg algebric si, cum ![]() intreg algebric T e +
intreg algebric T e +![]() intreg algebric si cum e rational T
intreg algebric si cum e rational T![]() I Z. Dar
I Z. Dar ![]() I 1, 1] T e
I 1, 1] T e![]() I
I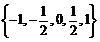 . Rezolvand pe rand ecuatiile, deducem ca p I
. Rezolvand pe rand ecuatiile, deducem ca p I
I. p = 2 T ep 1 T x,
y I R
si cum ![]() si m impar T
si m impar T![]() = 1, contradictie.
= 1, contradictie.
II. p = 4 T ep = i
si ![]() T k I cu
T k I cu
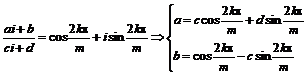 .
.
Rezolvand sistemul in sin![]() ,
, ![]() se deduce imediat
ca sin
se deduce imediat
ca sin![]() si
si ![]() I Q.
Fie z =
I Q.
Fie z = ![]() T zm = 1 T z
si
T zm = 1 T z
si ![]() intregi algebrici T z
+
intregi algebrici T z
+![]() = 2
= 2![]() intreg algebric si rational T
intreg algebric si rational T ![]() I
I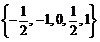 si cum sin
si cum sin![]() I Q T
I Q T
T 0 I ![]() . Daca sin
. Daca sin![]() = 0 T
= 0 T![]() I T
I T![]() .
.
Pentru a
= c T b
= d
(altfel x = y, nu) si din![]() T b = d T b = = d = 0 T x = y, nu. Deci a = c T
T b = d T b = = d = 0 T x = y, nu. Deci a = c T![]() = 1 T b = - d T
= 1 T b = - d T![]() T 1)m = 1, absurd
deoarece m e impar. Analog, din
T 1)m = 1, absurd
deoarece m e impar. Analog, din ![]() = 0 T 1)mim
= 1, absurd
deoarece im R
pentru m impar).
= 0 T 1)mim
= 1, absurd
deoarece im R
pentru m impar).
III. p = 3 T![]() . Alegem x = 2 + ep, y
= ep 1, m
= 3. Atunci
. Alegem x = 2 + ep, y
= ep 1, m
= 3. Atunci ![]() =
=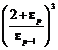 = ( ep 1)3 =
= ( ep 1)3 =![]() . Daca x = y T 3 = 0, nu. Daca
. Daca x = y T 3 = 0, nu. Daca ![]() T 2ep + 1 ep
1 T ep 2, nu. Deci p = 3 verifica.
T 2ep + 1 ep
1 T ep 2, nu. Deci p = 3 verifica.
IV. p = 6 T![]() Alegem x = 1 ep, y
= ep, m = 3.
Alegem x = 1 ep, y
= ep, m = 3.
Atunci ![]() =
=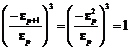 . Evident x y.
Daca
. Evident x y.
Daca ![]() =
=
= ![]() , absurd. Deci p =
6 verifica.
, absurd. Deci p =
6 verifica.
Asadar p I
O.L.85 din 9-10/2002
Sa se demonstreze ca daca xy + yz + zx = 1, unde x, y, z > 0, atunci
![]() . Cand se realizeaza maximul?
. Cand se realizeaza maximul?
Solutie. Deoarece x > 0, y > 0, z > 0,
rezulta ca exista a b g I![]() astfel incat
astfel incat
x =![]() , y =
, y =![]() , z = tg
, z = tg ![]() , a b g p, xy + yz + zx = =
, a b g p, xy + yz + zx = =![]()
![]() +
+![]() tg
tg ![]() +
+
+ tg ![]()
![]() = 1. Atunci
= 1. Atunci ![]()
= ![]() . Rezulta
. Rezulta ![]() ; egalitate pentru a b g =
; egalitate pentru a b g =![]() , de unde x = y =
z =
, de unde x = y =
z =![]() .
.
Observatie.
Din ![]()
![]() , deducem
, deducem ![]() ; analog
; analog ![]() ,
, ![]() .
.
Prin inmultire ![]() ; egalitate in triunghiul ABC
echilateral.
; egalitate in triunghiul ABC
echilateral.
P.78. Un elev a citit o carte in trei zile: vineri, sambata si duminica. Duminica a citit cu 100 de pagini mai mult decat vineri si sambata. Socotind, el a constatat ca a citit de 4 ori mai mult si inca 10 pagini decat vineri si sambata. Aflati cate pagini a citit in fiecare zi, daca vineri a citit de 2 ori mai multe pagini decat sambata.
P.79. Din ce numar trebuie scazut de 5 ori cate 5 pentru a obtine un numar mai mare cu de 5 ori cate 5 fata de dublul lui 5?
P.80. Daca Dan ar fi rezolvat inca 25 de probleme ar fi avut de 3 ori mai multe decat Alin. Impreuna au rezolvat 171 de probleme. Cate probleme a rezolvat fiecare copil?
P.81. Un elev l-a intrebat pe profesorul de matematica cati ani are. Profesorul i-a raspuns: "Daca voi mai trai inca un sfert din cati ani am trait si inca 5 ani, atunci voi avea 50 de ani. Afla cati ani am eu acum!"
P.82. Sa se afle trei numere naturale stiind ca suma lor este 46, iar jumatatea primului numar, triplul celui de-al doilea si al treilea micsorat cu 6 dau numere egale.
P.83. Pune paranteze si scrie semnele de operatie potrivite pentru a obtine egalitati matematice:
a) 123456 = 1;
b) 123456 = 0.
 P.84. Asezati
numerele de la 0 la 11 in cele 12 casute ale tabelei de mai jos, o
singura data, astfel incat suma pe linie si pe coloana
sa fie cea indicata.
P.84. Asezati
numerele de la 0 la 11 in cele 12 casute ale tabelei de mai jos, o
singura data, astfel incat suma pe linie si pe coloana
sa fie cea indicata.
V.175. Sa se arate ca suma numerelor naturale care impartite la 2003 dau catul 5 nu este patrat perfect.
V.176. Sa se arate ca 5n + 2002 nu este patrat perfect (n I N).
V.177. Calculati:
a) (52 + 325 : 910 : 27 - 260 : 420 : 85)10 : 128;
b) 20023 - 20022 2001 - 2002 2000 - 1999;
c) 56 22002 : (21999 + 21998 + 21997).
V.178. Fie multimile A = si B = . Determinati x, y I N astfel incat A = B.
V.179. Se dau numerele:
![]() si
si ![]() , n I N*
, n I N*
a) Pentru n = 2003, calculati A + B.
b) Aratati ca A + B - n + 1 = 0.
V.180. Scrieti multimea divizorilor lui n stiind ca:
n = 2003 - 203 (53 : 25 + 42 : 24 + 93 : 35) - 23.
V.181. Numerele naturale a, b verifica egalitatea: 7a + 11b = 1301. Sa se arate ca 118 < a + b < 183.
V.182. Sa se determine ultimele 9 cifre ale produsului: 1 2 3 34 35.
V.183. Comparati numerele: 67151 si 51199.
VI.161. Sa se reconstituie inmultirea:
* * * *
![]() * * * *
* * * *
2 0 0 3
* * * * *
* * * *
![]() * * * * *
* * * * *
* * * * 6 5 4 3
VI.162. Sa se probeze ca:
11 + 332 = 1100; 222 + 3332 = 111.111; 3333 + 33332 = 11112222;
555555 + 3333332 = 111111444444; 6666666 + 33333332 = 11111115555555;
77777777 + 333333332 = 1111111166666666;
888888888 + 3333333332 = 111111111777777777;
9999999999 + 33333333332 = 11111111118888888888.
VI.163. Rezolvati in N ecuatia: ab - 4a + 3b = 155.
VI.164. Sa se cerceteze daca
exista patrate perfecte de forma ![]() .
.
VI.165. Determinati numarul natural care are trei divizori, a caror suma este 57.
VI.166. Determinati numerele nenule x, y,
z stiind ca sunt invers
proportionale respectiv cu 2, 3, 4 si ![]() .
.
VI.167. Sa se arate ca exista numere naturale care au ultimele cifre 2002 si sunt divizibile cu 2003.
VI.168. In triunghiul dreptunghic ABC (m( A) = 90 ) construim bisectoarea unghiului B care taie (AC) in D si perpendiculara din A pe acesta taie (BC) in E. Sa se demonstreze ca:
a) DE BC;
b) BC AE = AC BD.
VII.187. Fie triunghiul oarecare ABC, M
mijlocul lui BC si O mijlocul lui AM. Sa se gaseasca valoarea raportului ![]() .
.
VII.188. Fie numerele:
![]()
![]() .
.
Aflati
cel mai mic numar x I N* pentru care
![]() I N.
I N.
VII.189. In triunghiul ABD, C I [BD], iar bisectoarea ACD este perpendiculara pe AD si intalneste bisectoarea ABC in punctul E.
a) Stiind ca EC AB si m (BEC) = 30 , stabiliti natura patrulaterului ABCE.
b) Stiind ca BD = 12 cm, calculati lungimile segmentelor [OE] si [OB], unde = BE AD.
VII.190. Sa se arate ca ![]() Q, n I N.
Q, n I N.
VII.191. Pe baza [BC] a triunghiului ABC isoscel se alege un punct oarecare D prin care se duce paralele la laturile congruente ale triunghiului. Sa se arate ca perimetrul paralelogramului format nu depinde de pozitia punctului D.
VII.192. Fie paralelogramul ABCD, cu M si N mijloacele laturilor DC respectiv BC. Daca = BM DN, = AM ND si = BM AN, atunci:
a) Sa se arate ca EF BD.
b) Sa se calculeze ![]() .
.
VIII.143. Determinati functiile f : R R cu urmatoarele proprietati:
i) f (x) = ax + b, x I R
ii) f (f (x)) = bx + a, x I R
iii) f (1) = 2002 sau f (-1) = 2003.
VIII.144. Se considera un punct M in interiorul unghiului XOY de masura 30 . Din punctul M se duc perpendicularele MA OX si MB OY cu A I [OX, B I I [OY. Se considera apoi punctul D, mijlocul segmentului [OM], in care se ridica perpendiculara VD pe planul unghiului XOY. Daca [OM] = [VD] = a > 0, sa se calculeze distanta de la punctul V la dreapta AB.
VIII.145. Daca a I R, a 1 sa se compare numerele: 2a si ![]() +
+ ![]() .
.
Pot sa fie egale? Justificati raspunsul.
VIII.146. Se da cubul ABCDA B C D . Se cere unghiul dintre dreptele DA si BD
VIII.147. Fie M, N, P, Q pentru puncte necoplanare astfel incat MN = MP =
= MQ = 6 cm si m (MNQ) = 30 ; m (MPQ) = 45 si m (NMP) = 60
a) Demonstrati ca triunghiul NPQ este dreptunghic.
b) Determinati pozitia unui punct R pe muchia MP astfel incat perimetrul triunghiului NQR sa fie minim.
VIII.148. Sa se determine numerele
prime x, y, z stiind ca x + 3y
+ 5z = 2044 iar x este solutia ecuatiei: ![]() .
.
VIII.149. a) Rezolvati ecuatia: x + 1 x - 2
b) Pentru a 0, rezolvati ecuatia: ax + b ax + c , b, c I R.
IX.193. Aratati ca triunghiul ABC este echilateral daca si numai daca:
![]() .
.
IX.194. Fie f : R R o functie cu proprietatile:
i) exista T > 0 astfel incat f (x + T) = f (x), x I R
ii) f (x) - f (y) x - y x, y I [0, T].
Sa se arate ca f (x) - f (y) x - y x I R.
IX.195. Daca a, b, c, d I N*, sa se demonstreze inegalitatea:
![]() .
.
IX.196. Sa se determine functiile f : R R pentru care f (0) = 0 si
f (f 2(x) + f 2(y)) = x2 + y2, x, y I R.
IX.197. Se considera ecuatia: ax2 + b x + c = 0, a I R*, b, c I R. Determinati conditia necesara si suficienta pentru ca ecuatia sa aiba solutie unica.
IX.198. Calculati ![]() .
.
X.199. Sa se rezolve ecuatia:
![]() .
.
X.200. Fie f : N* Z* astfel incat f (1) f (2) = 2 si
![]()
![]() , n I N*.
, n I N*.
Sa se determine f (n), n I N*.
X.201. Fie (xn)n 1 un sir de numere reale strict pozitive si distincte. Sa se arate ca (xn)n 1 este o progresie geometrica daca si numai daca:
![]() , n 2.
, n 2.
X.202. Se considera polinoamele f, g
I Q [X] pentru care gr f = 5, gr g I ![]() si f (0) = g(0), f (1 + i) = g(1
+ i), f (1 +
si f (0) = g(0), f (1 + i) = g(1
+ i), f (1 + ![]() ) = g(1 +
) = g(1 + ![]() ). Sa se determine suma radacinilor
ecuatiei polinomiale f (x) = 0.
). Sa se determine suma radacinilor
ecuatiei polinomiale f (x) = 0.
X.203. Aratati ca
daca z I C*
si ![]() , atunci
, atunci ![]() .
.
X.204. Daca x, y, z I C* distincte doua cate doua astfel incat x y z = 1 si (x + y + z)5 = (y + z - x)5 + (x + z - y)5 + (x + y - z)5 sa se calculeze x + y + z
X.205. a) Fie x, y, z I (0, ), y 1. Sa se arate ca ![]() .
.
b) Folosind eventual punctul a), sa se ordoneze crescator numerele:
![]() ,
, ![]() ,
, ![]() , unde a, b, c
I R, 0 < a < b < c < 1.
, unde a, b, c
I R, 0 < a < b < c < 1.
XI.185. Calculati:
a) ![]() ; b)
; b) ![]() .
.
XI.186. Daca x1, x2 sunt radacinile ecuatiei x2 + x + 1 = 0, sa se arate ca:
![]() .
.
XI.187. Daca A, B I M2(R) sa se arate ca:
det[(AB + BA)4 + (AB - BA)4] 0.
XI.188. Sa se calculeze: ![]() .
.
XI.189. Sa se arate ca
ecuatia ![]() , n I [0, 1], n I N* admite o
singura solutie xn
si
, n I [0, 1], n I N* admite o
singura solutie xn
si ![]() .
.
XI.190. Fie sirul: 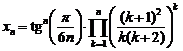 . Sa se calculeze
. Sa se calculeze ![]() .
.
XI.191. Fie a I ![]() si sirul (xn)n 1 cu x1 > 0 si xn
+ 1 =
si sirul (xn)n 1 cu x1 > 0 si xn
+ 1 = ![]() , n I I N*.
Sa se calculeze
, n I I N*.
Sa se calculeze ![]() .
.
XI.192. Fie matricea A I M3(R), 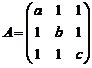 .
.
1) Daca abc = 1 si a, b, c I (0, ) sa se arate ca det A 0, det A* 0 si det (A*)* 0.
2) Pentru a = b = c, calculati (A*)n, n I N*. (A* este adjuncta matricei A).
XI.193. Fie sistemul: 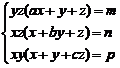 , in care a, b, c,
m, n, p sunt numere reale.
Sa se arate ca daca determinantul
, in care a, b, c,
m, n, p sunt numere reale.
Sa se arate ca daca determinantul 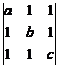 este nenul, acesta
este o conditie suficienta pentru ca sistemul sa admita cel
putin o solutie reala.
este nenul, acesta
este o conditie suficienta pentru ca sistemul sa admita cel
putin o solutie reala.
Afirmatia ramane valabila in cazul unui sistem analog cu patru necunoscute?
XII.148. Fie f : [0, 1] R, f (x) = (x2 +1)ex.
Calculati: 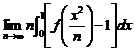 .
.
XII.149. Fie M multimea functiilor polinomiale p(x), de gradul trei care sunt nenegative pe [0, 1]. Se cere sa se gaseasca cel mai mic numar l astfel ca:
![]() , oricare ar fi p I M.
, oricare ar fi p I M.
XII.150. Fie f : ![]() R o functie de doua ori derivabila astfel incat
R o functie de doua ori derivabila astfel incat
f (x) cos x 2f (x) sin x, x I ![]() . Sa se arate ca:
. Sa se arate ca:
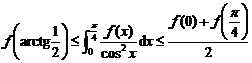 .
.
XII.151. Fie G un grup si H un subgrup propriu al sau. Daca exista a I G H cu proprietatea ca Ha = H este subgrup al lui G, sa se arate ca ord a = 4.
XII.152. Fie f : R (0, ) o
functie integrabila astfel incat ![]() . Sa se arate ca
. Sa se arate ca ![]() .
.
XII.153 Sa se calculeze: ![]() .
.
XII.154. Fie f, P, Q : [-1, 1] R continue. In plus:
1) f - para;
2) P - para si nenula;
3) Q - impara.
Atunci: ![]() .
.
XII.155. Dati un exemplu de un corp care admite doua automorfisme.
OG.68. Aflati toate numerele de
forma ![]() care au exact 4
divizori intregi, astfel incat
care au exact 4
divizori intregi, astfel incat ![]() I N.
I N.
OG.69. Fie a, b, c I R* astfel
incat a3 + b3 + c3 = 2abc.
Sa se arate ca exista
x I R astlfe
incat:
(ax + b)(bx + c)(cx + a) > (ax2 + 2bx + c)(bx2 + 2cx + a)(cx2 + 2ax + b)
OG.70. Daca x, y, z I (0, )
si m, n, p I N* fixate,
sa se calculeze minimul expresiei: ![]() .
.
OG.71. In coltul din stanga-jos a unui tabel patratic de 5 5 se afla o broscuta. Ea poate sari in orice casuta adiacenta (cu o latura comuna). Este posibil ca broscuta sa treaca prin toate casutele exact o data si sa se intoarca de unde a plecat?
OL.100. Fie A = si m 40425. Alegem A1, , Am A cu cate 4 elemente, astfel incat oricare doua au cel mult 2 elemente comune. Sa se arate ca exista printre submultimile alese 49 astfel incat reuniunea lor este A, dar reuniunea oricaror 48 este diferita de A.
OL.101. Sa se determine functiile f : Z Z cu proprietatile:
a) f (xy) = f (x) f (y), x, y I Z
b) f (x2 + y2)
= ![]() , x, y I Z.
, x, y I Z.
(unde [x] este partea intreaga a lui x).
OL.102. Fie a1, a2, , an numere reale strict pozitive. Sa se demonstreze inegalitatea:
![]() , unde m, n I N*.
, unde m, n I N*.
OL.103. Determinati cel mai mare numar natural n pentru care exista o multime A cu n elemente cu proprietatea ca a I A T 2a A.
OL.104. Daca a, b, c sunt numere reale strict pozitive
si n este un numar natural,
atunci ![]()
![]() .
.
(In legatura cu problema 24477 din G.M. nr. 3/2001, autor Ion Nedelcu)
OL.105. Fie triunghiul ABC inscris in cercul C = C (O, R) astfel incat dreapta AO separa punctele B, C. Tangenta la cercul C in punctul T diametral opus punctului A taie dreapta BC in punctul S. O dreapta d care trece prin O taie dreptele BA si CA in punctele X respectiv Y. Sa se arate ca OX = OY daca si numai daca S I XY.
1. Un con circular drept construit din
folie de aluminiu are inaltimea de ![]() cm. Stiind
ca sectiunea axiala a conului este un triunghi echilateral,
aflati:
cm. Stiind
ca sectiunea axiala a conului este un triunghi echilateral,
aflati:
a) raza si generatoarea conului;
b) aria laterala, aria totala si volumul conului;
c) daca se suspenda conul intr-un vas ce contine o solutie de AgNO3, dupa un timp, prin cantarire se constata ca masa corpului a crescut cu 11 g. Cati atomi de Al si de Ag au participat la reactia chimica?
2. Pentru ora de matematica, un elev construieste o piramida patrulatera regulata din sarma de cupru cu = 3 mm. Stiind ca piramida are inaltimea de 8 cm si apotema de 10 cm, calculati masa piramidei. Se stie ca rCu = 8,79 g/cm3.
Ziarele londoneze au publicat nu demult un interviu cu un astrolog si un chiromant foarte cautat. Spicuim din acest interviu:
"- Si nestematele, maestre, n-au si ele avantaje si dezavantaje?
- Desigur! totul depinde de culoare parului persoanei careia i se ofera giuvaerul. Niciodata nu se va darui aceeasi piatra unei blonde si unei brunete.
Insusi metalul are influenta deoarece este bun conducator de bucurii si de necazuri. Brunetelor le vor fi oferite bijuterii la care sa predomine argintul, caci acest metal le va da un plus de inspiratie, de fantezie. Brunetele fiind de obicei mai pozitive, argintul le va completa ceea ce le lipseste: dragostea pentru un ideal si poezie.
- Si blondelor?
- Blondele sunt impulsive, caci ele se afla sub influenta lunii. Sunt cum se spune "lunatice . Ele nu au nevoie sa fie indrumate spre un ideal. Li se vor darui bijuterii la care aurul are ponderea cea mai mare, caci aurul calmeaza fanteziile si exagerarile.
- Asta in privinta monturii! dar despre pietre?
- Blondelor sa li se ofere rubine sau granate, pietrele intelepciunii, care actioneaza ca niste frane asupra instinctelor. Brunetele au nevoie de ametist, care este piatra sperantei, sau smaraldul aducator de noroc; topazul este excelent pentru blonde ca si peruzeaua si safirul.
- Dar diamantul?
- Toata lumea il poate purta! este piatra elegantei, fara proprietati favorabile, dar si fara pericole.
BUCURESTI Lic. teoretic "Alexandru Vlahuta": cls a V-a: Dobrescu-Marandei Monica Ioana (8), Gheorghe Andreea (20), Iacobescu Flavia (12), Istrate Dana (6), Negoescu Cristina (10), Zlate Nicoleta (8); cls a VII-a: Oprescu Madalina (4). Sc. gen. Nr. 12: cls. a VII-a: Apostolescu Alin (6).
CAMPULUNG-MUSCEL (jud. Arges): Sc. gen. "Sf. Iacob": cls. a VII-a: Hoaghea Marius (6), Hunyadi Iolanda (12), Mirzac Diana Andreea (14), Stoica Catalina (8), Serbanoiu Eduard (14), Trusca Alexandra (8), Zarnescu Ilona (8).
DEJ (jud. Cluj): Lic. Sc. gen. Nr. 2: cls. a III-a: Albu Tatiana (9); cls. a V-a: Rus Bogdan (6).
HUNEDOARA (jud. Hunedoara): Lic. "Iancu de Hunedoara": cls. a VI-a: Alexandru Giurgiu (4); cls. a VIII-a: Mares Anca (4), Schiopu Liana (4).
LUGOJ (jud. Timis): Sc. gen. Nr. 4: cls. a V-a: Eftimie Daniel (14); Ilinoi Samuel (7); Popescu Denisa (4); cls. a VI-a: Eremia Dan (11), Ghencian Adrian (6), Ghencian Daniel (6), Homei Andreea (8), Iacobescu Roxana (8), Jurj Filip (5), Popescu Bogdan (6), Svetlak Andrada (7); cls. a VIII-a: Eftimie Daniel (14); Laudacescu Florin (5); Pelcea Calin (9) Ursulescu Andreea (7).
PAULESTI (jud. Prahova): Sc. Gen. cu clasele V-VIII cls. a V-a: Enache Anca (10), Jipa Mihai (9), Pirvulescu Paula (4), Stoian Stefania (3), Zamfir Andra-Maria (10).
RAMNICU VALCEA (jud. Valcea): C. N. "Al. Lahovary" cls. a V-a: Botu Andreea (4), Gainariu Sorina Diana (4).