
|
|
|
ECUATII DIFERENTIALE
ECUATII DIFERENTIALE DE ORDINUL INTAI![]()
a) O ecuatie de forma
![]()
![]() ,
, ![]() (1)
(1)
unde ![]() e o functie
necunoscuta , se numeste ecuatie diferentiala de
ordinul intai (prescurtat e.d.).
e o functie
necunoscuta , se numeste ecuatie diferentiala de
ordinul intai (prescurtat e.d.).
b) Functia ![]() unde
unde ![]() este un interval se
numeste solutie a ecuatiei diferentiale
(1) daca si numai daca
este un interval se
numeste solutie a ecuatiei diferentiale
(1) daca si numai daca ![]() este
derivabila pe
este
derivabila pe![]() si
si ![]() ,
, ![]()
c) Graficul functiei ![]() este o curba
plana ce se numeste curba integrala
este o curba
plana ce se numeste curba integrala
d) Solutia generala a ecuatiei (1) este o functie derivabila
![]() ,
, ![]() ,
, ![]() (2)
(2)
care este solutie a ecuatiei (1)
pentru orice constanta ![]() . Graficul solutiei generale (2) este o familie de curbe
plane numite curbe integrale . A rezolva e.d. (1) inseamna a gasi
solutia generala (2) .
. Graficul solutiei generale (2) este o familie de curbe
plane numite curbe integrale . A rezolva e.d. (1) inseamna a gasi
solutia generala (2) .
e) Daca solutia generala a ecuatiei (1) se poate calcula cu ajutorul primitivelor functiilor elementare atunci e.d. (1) se numeste integrabila prin cuadraturi
f) Se numeste solutie particulara a ecuatiei (1) o functie
![]() (3)
(3)
care se obtine din solutia
generala (2) pentru ![]() .
.
g) Problema lui Cauchy pentru o e.d. (1) este formata din ecuatia (1) plus o conditie (initiala)
![]()
![]()
A o rezolva inseamna a gasi
solutia particulara (3) care satisface conditia ![]() , adica a
gasi
, adica a
gasi ![]() astfel incat
astfel incat ![]() . Constanta
. Constanta ![]() se inlocuieste in
solutia generala (2) si se gaseste solutia
particulara (3) a problemei Cauchy .
se inlocuieste in
solutia generala (2) si se gaseste solutia
particulara (3) a problemei Cauchy .
h) Se numeste solutie singulara a ecuatiei (1) o solutie care nu poate fi obtinuta din solutia generala (2) pentru nici o valoare a constantei C .
A. Ecuatii diferentiale de ordinul 1
rezolvate (sau rezolvabile) in raport cu ![]()
![]() ,
, ![]() ,
, ![]() (4)
(4)
Daca ![]() e solutie a
ecuatiei (4) cu graficul
e solutie a
ecuatiei (4) cu graficul ![]() , atunci in fiecare punct
, atunci in fiecare punct ![]() panta tangentei la
grafic este
panta tangentei la
grafic este ![]() . Deci ecuatia (4) defineste o familie de curbe cu
aceasta proprietate .
. Deci ecuatia (4) defineste o familie de curbe cu
aceasta proprietate .
Teorema de existenta si unicitate pentru ecuatii diferentiale de ordinul 1
Fie punctul ![]() in plan si fie
ecuatia
in plan si fie
ecuatia ![]() ,
, ![]() ,
, ![]() . Daca
. Daca ![]() este Lipschitziana in a doua variabila , adica
exista
este Lipschitziana in a doua variabila , adica
exista ![]() astfel incat
astfel incat ![]() ,
, ![]() , atunci exista
, atunci exista ![]() si
exista o unica functie
si
exista o unica functie![]() astfel incat
astfel incat ![]() e solutie a
ecuatiei (4) si satisface conditia
e solutie a
ecuatiei (4) si satisface conditia ![]() (
(![]() e solutie a problemei Cauchy ). Altfel spus , prin
e solutie a problemei Cauchy ). Altfel spus , prin ![]() trece o singura
curba integrala .
trece o singura
curba integrala .
![]() (5)
(5)
![]() ,
, ![]()
Aceasta este solutia generala a ecuatiei (5) .
Caz particular. ![]() . Ecuatia devine
. Ecuatia devine ![]() de unde
de unde ![]() ,
, ![]() .
.
I Ecuatii cu variabile separabile
![]() (6)
(6)
unde ![]() ,
, ![]() ,
, ![]() intervale . Impartim ecuatia cu
intervale . Impartim ecuatia cu ![]() (daca sunt
nenule) . Ecuatia se scrie
(daca sunt
nenule) . Ecuatia se scrie
![]()
integram si gasim ![]() ,
, ![]() .
.
II. Ecuatii care provin din diferentiale totale (ecuatii diferentiale exacte)
![]() (7)
(7)
unde
functiile ![]() admit
derivate partiale continue pe D si verifica conditia
admit
derivate partiale continue pe D si verifica conditia
![]() (8)
(8)
Atunci exista
functia ![]() ,
, ![]() , continua , cu derivate partiale de ordinul doi
continue pe D astfel incat
, continua , cu derivate partiale de ordinul doi
continue pe D astfel incat
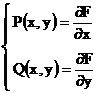 (9)
(9)
Egalitatea (8)
exprima relatia ![]() . Atunci ecuatia (7) se poate scrie
. Atunci ecuatia (7) se poate scrie
![]()
adica ![]() de unde se
obtine ca solutia generala a ecuatiei este
de unde se
obtine ca solutia generala a ecuatiei este
![]() , k = const.
, k = const.
Pentru a afla functia F se pot folosi doua metode :
Metoda 1. Se integreaza una din ecuatiile din sistemul (9) , de exemplu prima :
![]()
Formula obtinuta
se deriveaza in raport cu y si din ![]() se
gaseste
se
gaseste ![]() de unde se
obtine prin integrare
de unde se
obtine prin integrare ![]() si apoi
si apoi ![]() .
.
Metoda 2.
Se foloseste direct formula urmatoare , unde ![]()
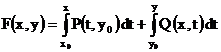
III. Ecuatii care pot fi transformate in ecuatii diferentiale exacte
Factor integrant
Sunt ecuatii de
tip (7) pentru care nu este satisfacuta conditia (8) . Atunci se
cauta un factor integrant , adica o functie ![]() cu care se
inmulteste ecuatia (7) :
cu care se
inmulteste ecuatia (7) :
![]() (8
(8
Pentru ca ecuatia (8 ) sa fie o e.d. exacta se impune sa se verifice conditia
![]() (9 )
(9 )
![]()
![]()
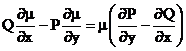
S-a obtinut o ecuatie cu variabile
separate din care se afla ![]() , se inlocuieste in (8 ) si se
procedeaza ca la ecuatia diferentiala exacta .
, se inlocuieste in (8 ) si se
procedeaza ca la ecuatia diferentiala exacta .
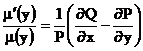
![]()
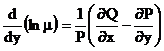
Se afla ![]() , se inlocuieste in (8 ), care este o
ecuatie diferentiala exacta .
, se inlocuieste in (8 ), care este o
ecuatie diferentiala exacta .