Functii derivabile de o variabila reala

Functii derivabile de o variabila reala

Definitia1

a)     Spunem ca f are derivata in punctul a daca:

(1) () 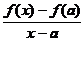=f'(a)

b)     Daca, in plus, derivata f'(a) exista si este finita vom spune ca f este derivabila in punctul a.

Observatii!

1)Problema existentei derivatei unei functii se pune numai in puncte care apartin multimii de definitie a functiei si care nu sunt puncte izolate.

2)Derivabilitatea are caracter local, adica in studiul derivabilitatii unei functii intr-un punct este suficient a fi cunoscute numai valorile functiei dintr-o vecinatate a acelui punct.

3)In loc de (1), adeseori vom scrie, notand x-a=h, (2) f'(a)=.

Interpretarea geometrica a derivatei

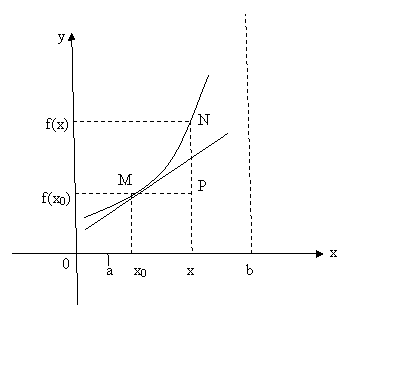
Fie f:(a,b)R, f este derivabila inntr-un puinct x₀(a,b) ( =f'(x₀)

x₀ este punctul in care calculez derivata

x este un punct variabil

-graficul lui f are tangenta in punctul (x₀,f(x₀)) si anume dreapta de ecuatie

y-f(x₀)=m(x-x₀), m=panta tangentei

m=f'(x₀)=coeficientul unchiular al tangentei in punctual (x₀,f(x_o))

Observatie!

Daca f'(x₀)= in sensul ca = rezulta ca tangenta in punctul (x₀,f(x_o)) este paralela cu axa oy.

Definitia2

a)Daca functia f:DR (DR) este derivabila in orice punct al unei submultimi A a lui D, atunci spunem ca f este derivabila pe A

b)In acest caz , functia definita pe A cu valori reale care asociaza fiecarui punct xA, derivata f'(x) in punctul x se numeste derivata lui f pe multimea A si se noteaza cu f'.

Operatia prin care obtinem functia f' se numeste operatie de derivare a lui f.

Observatie! Daca y=f(x), adeseori se scrie (3) y'=f'(x) sau y'=

Exemplu

Fie f:RR , f(x)=

Sa se studieze continuitatea si dereivabilitatea.

f- continua in x₀R, daca () f(x)=f(x₀)

Definitia cu siruri:

R cu x_nx₀ , x_nx₀ f(x_n)f(x₀).

Fie R, a_nx₀ , x₀R

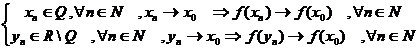
a_n: f(a_n)f(x₀).

Fie x₀R si Q, x_nx₀

f(x_n)=sinx_nsinx₀

Fie x₀R si RQ , y_nx₀

f(y_n)=y_nx₀

sinx₀ =x₀ x₀=0 f- continua in x₀=0

f- derivabila in x₀ daca () =f'()R

x₀=0

Fie Q , x_n0

R

Fie RQ , y_n0

R

Pornind de la definitia1 vom introduce notiunea de diferentiala a unei functii

Fie D un interval deschis din R si f:DR o functie derivabila intr-un punct aD.

Atunci conform definitiei1 avem (4)() =f'(a)R.

Sa notam cu (5) (x)=f'(a)- ,pentruxa ( () xD)

Cum functia f este derivabila in punctul a () (x)=0(adica prelungesc functia atingand valoarea 0)

Din relatia (2) avem:

(6) f(x)-f(a)=f'(a)(x-a)+(x)(x-a), () xD, luand prin definitie (a)=0.

Observam ca, daca x se apropie de" a" , diferenta f(x)-f(a) se poate aproxima prin f'(a)(x-a), adica(7) f(x)-f(a)f'(a)(x-a).

Daca notam x-a=h, atunci relatia (6) se mai scrie:

(6') f(a+h)-f(a)=f'(a)·h+(a+h)·h, unde a+hD

Pentru valori ale lui h suficient de mici, diferenta f(a+h)-f(a)f'(a)·h, unde a+hD

Aceasta arata ca , intr-o vecinatate a unui punct de derivabilitate a functiei, functia are o comportare liniara.

Fie D un interval deschis al lui R si fie f:DR, o functie definite pe D.

Defintia3

a)Spunem ca f este diferentiabila in punctual a daca () un numar real A (care depinde de f si a) si o functie :DR cu proprietatea cu (x)=0a.i.

(8) f(x)-f(a)=A(x-a)+(x)(x-a), () xD

b)Spunem ca functia f este diferentiabila pe D daca f este diferentiabila in orice punct aD.

Interpretarea geometrica a diferentialei

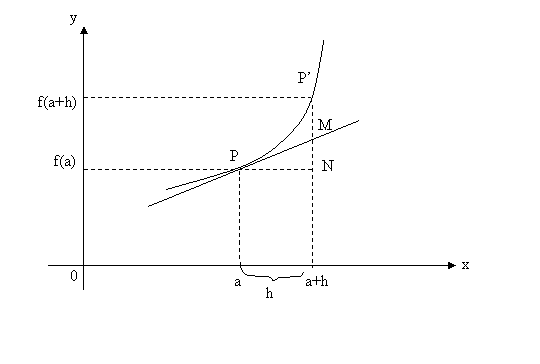
Observam ca h=dx(h) este lungimea catetei PN din triunghiul dreptunghic PNM, f'(a)=tg, diferentiala functiei f in punctual a calculate in h este f'(a)·h, adica lungimea catetei MN iar diferenta f(a+h)-f(a) este lungimea segmentului P'N.Daca h este suficient de mic, atunci segmentele P'N si MN sint "aproximativ" egale.Aceasta ne spune ca in jurul punctului P graficul functiei se poate aproxima cu o portiune a tangentei.

Tinand seama de definitia diferentialei se obtin imediat din regulile uzuale de derivare urmatoarele reguli de diferentiere:

Daca f,g:DR sunt functii derivabile pe un interval deschis D al lui R, atunci:

(I)d(f+g)=(f+g)'dx=(f'+g')dx=f'dx+g'dx=df+dg;

(II) d(f)=(f)'dx=f'dx=df, r;

si daca, in plus, g0, atunci

(III) d(

Ex

Teorema1 Fie f:DR , DR si aDD'

Atunci f este diferentiabila in punctual a f este derivabila in punctual a

Dem:

Necesitatea :pp f diferentiabila in a f derivabila in a

Cum f este diferentiabila in punctual a () constanta AR si () :DR cu (x)=0 (este continua) a.i.f(x)-f(a)=A(x-a)+(x)(x-a), () xD

Luam xD si impartim ambii membrii ai egalitatii prin x-a )xD

Cum f diferentiabila () () A=derivate functiei A=f'(a) f derivabila in punctual a

Suficienta: pp f derivabila in a f diferentiabila in a

Cum f derivabila in punctual a ()=f'(a)R

Consideram urmatoarea functie auxiliara

(*)

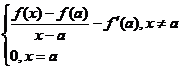
Observam ca : (x)=[]=0=(a), (adica este continua in punctual a)

Din definitia lui rezulta pentru xa are loc: f(x)-f(a)=f'(a)(x-a)+(x)(x-a), (aceasta egalitate este verificata si pentru x=a) f diferentiabila in punctual a iar A=f'(a).

Definitia4

Fie f:DR, aDD' si f derivabila in punctual a.

Se numeste diferentiala functiei f in punctual a, functia liniara T:R R, definite prin:

(9) T(h)=f'(a)·h, () hR

Vom nota diferentiala cu df(a) si atunci vom avea (9') df(a)(h)=f'(a)·h, hR

Atunci relatia (7) se mai poate scrie (10) f(a+h)-f(a)df(a)(h)

Observatie!

1)In timp ce derivate functiei f in punctual a este un numar, diferentiala lui f in a este o functie liniara.

2)Se observa usor ca functiile liniare T:RR, sunt functii de forma T*h=A*h, () hR, unde A=constanta reala.

Daca L(R)=multimea tuturor functiilor liniare de la R la R.

Definim functia φ:L(R)R data prin φ(T)=A, daca T*h=A*h, () hR.

Φ este bijectivase face posibila identificarea unei functii liniare (T:RR) cu un numar real(tocmai coeficientul functiei liniare) si reciproc.

Ex

Avand in vedere aceste observatii dam urmatoarea definitie:

Definitia5

Fie f:DR, DR si aDD'

Spunem ca f este diferentiabila in punctul a daca () o aplicatie liniara T:RR a.i.

=0,

sau

(11) f(x)=f(a)+T(x-a)+(x)(x-a), xD, unde :DR cu proprietatea ca (x)=0

Definitia6

Fie ARⁿ. Un punct x₀Rⁿ spunem ca este punct de acumulare pentru multimea A, daca VV(x₀) (V)AØ( in orice vecinatate a lui x₀ () cel putin un punct din D)

Exemplu

Definitia7

Numim sistem de numere reale o multime R inzestrata cu doua operatii algebrice +(adunarea)((x,y)x+y) si ·(inmultirea)((x,y)x·y) si cu o relatie de ordine notata "≤", care satisface urmatoarele trei grupe de axiome:

I.R este un corp , adica:

(I.1) x+(y+z)=(x+y)+z pentru orice x,y,zR;

(I.2) x+y=y+x pentru orice x,yR;

(I.3) exista un element 0R asa incat 0+x=x pentru orice xR;

(I.4) pentru orice element xR exista un element -xR asa incat x+(-x)=0;

(I.5) x·(y·z)=(x·y)·z pentru orice x,y,zR;

(I.6) x·y=y·x pentru orice x,yR;

(I.7) exista un element 10 in R asa ca 1·x=x, pentru orice xR;

(I.8) pentru orice xR, x0, exista un element x^-1R(notat si 1/x) a.i. x·x^-1=1;

(I.9) x·(y+z)=x·y+x·z pentru orice x,y,zR;

II. R este un corp ordonat, adica:

(II.1) x ≤ y si y ≤ z x ≤ z;

(II.2) x ≤ y si y≤ x x=y;

(II.3) pentru orice x,yR are loc sau x ≤ y sau y≤ x;

(II.4) daca x ≤ y, atunci x+z ≤ y+z pentru orice zR;

(II.5) daca x ≤ y si 0 ≤ z, atunci x·z ≤ y·z.

III.      Axioma de completitudine(Cantor-Dedekind)

Orice submultime nevida A a lui R care este majora admite cel putin o margine superioara.Cu alte cuvinte, exista supA si supAR.

Vom nota prin =R si se numeste dreapta reala incheiata sau compactificata