
|
|
|
Locuri geometrice remarcabile
CERCUL
In geometria euclidiana, cercul este multimea tuturor punctelor egal departate de un punct fix numit centru. Circumferinta unui cerc este de fapt lungimea cercului. Arcul de cerc este orice portiune continua a unui cerc.
![]()
unde A este aria cercului, r este raza cercului, d este diametrul cercului, iar π este o constanta matematica.
![]()
![]()
unde Asect este aria sectorului de cerc,r este raza cercului, n este unghiul sectorului de cerc masurat in grade, iar π este o constanta matematica.
![]()
unde Larc este lungimea arcului de cerc,r este raza cercului, n este unghiul sectorului de cerc masurat in grade, iar π este o constanta matematica.
ELIPSA
Elipsa (din gr. elleipsis - lipsa) este curba plana definita ca locul geometric al punctelor pentru care suma distantelor la doua puncte fixe (numite focarele elipsei) este constanta. Aria elipsei de semiaxe a si b este A = πab.
Elipsa este o conica, adica este una dintre curbele care se pot obtine prin intersectia dintre un con si un plan.
Din punct de vedere algebric, elipsa este o curba definita in coordonate carteziene de urmatoarea ecuatie:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
cu conditiile B2 < 4AC, toti coeficientii sunt reali si exista mai mult de o singura pereche (x, y) care sa satisfaca ecuatia.
Segmentul de dreapta care trece prin focare si are capetele pe elipsa se numeste axa majora. Segmentul perpendicular pe mijlocul axei majore si avand capetele pe elipsa se numeste axa minora.
Parametrul
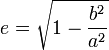 care apare si in figura
alaturata se numeste excentricitatea elipsei.
care apare si in figura
alaturata se numeste excentricitatea elipsei.
Lungimea elipsei este data de o integrala eliptica. Elipsa cu excentricitatea e si cu semiaxa mare a va avea lungimea
![L = 2pi a left[right)^2e^2 - left(right)^2 - left(right)^2 - dots}right]!,](../../files/matematica/80_poze/image006.gif)
Se poate observa ca cercul este un caz particular de elipsa (elipsa in care cele doua focare coincid - sau pentru ecuatia algebrica, elipsa pentru care A = C si B = 0).
O elipsa centrata in originea sistemului de coordonate si avand una dintre axe orizontala poate fi parametrizata astfel:
![]()
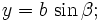
unde β apartine intervalului ![]()
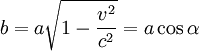 ,
unde α poate fi interpretat ca fiind unghiul cu care se
roteste reperul minkowskian al cercului datorita deplasarii
cu viteze relativiste.
,
unde α poate fi interpretat ca fiind unghiul cu care se
roteste reperul minkowskian al cercului datorita deplasarii
cu viteze relativiste. HIPERBOLA
Hiperbola, (din greaca ὑπερβολή, 'aruncat peste') este o curba plana, facand parte din familia conicelor (numita adeseori conica deschisa), ce poate fi definita echivalent in oricare din urmatoarele moduri:
Orice hiperbola este formata din doua parti neconectate, numite ramurile hiperbolei. Fiecare ramura este o curba deschisa infinita.