|
|
|
POLIGOANE
Def: Se numeste poligon o figura geometrica formata din "n" laturi sau linii frante inchise (n=nr.laturi).
●Se numeste poligon convex , poligonul care are varfurile orientat cu unghiurile interioare spre exterior .
●Se numeste poligon concav,poligonul care are un varf orientat cu unghiul interior catre interiorul poligonului.
Poligoanele convexe regulate sunt poligoanele care au toate laturile congruente.
*Suma unghiurilor intr-un poligon se calculeaza cu formula (n-2)·180 , unde n=nr. laturi.
*Perimetrul unui poligon se calculeaza insumand lungimile laturilor poligonului.
*Aria unui poligon reprezinta totalitatea punctelor din interiorul acestuia.
*CLASIFICARE:
Poligonul cu trei laturi se numeste triunghi. ; Poligonul cu sapte laturi se numeste heptagon.
Poligonul cu patru laturi se numeste patrulater. ; Poligonul cu opt laturi se numeste octogon.
Poligonul cu cinci laturi se numeste pentagon. ; Poligonul cu noua laturi se numeste nonagon.
Poligonul cu sase laturi se numeste hexagon.; Poligonul cu zece laturi se numeste decagon.
Def:Patrulaterul reprezintaun poligon convex cu patru laturi.
n=4
laturi 
suma unghiurilor dintr-un patrulater (4-2)·180s=360s
Clasificare:
a)Paralelogramul d)Patratul
b)Dreptunghiul e)Trapezul
c)Rombul
Def:Paralelogramul reprezinta un patrulater care are laturile opuse paralele.
Daca ABCD este paralelogram rezulta proprietatile :
A B *AB || CD *AB
CD
*AD ||
BC *ADBC
O * <A = <C = unghiuri obtuze
* <B = <D = unghiuri ascutite
*Diagonalele se injumatatesc OAOC , OBOD
DMC
●Perimetrul PABCD = AB+BC+CD+DA = 2AB +2BC
●Aria unui paralelogram este egala cu produsul dintre lunrimea unei laturi si inaltimea corespunzatoare : AABCD = DC · AM .
Conditia necesara si suficienta pentru ca un patrulater sa fie paralelogram este ca punctul de intersectie el diagonalelor sa fie mijlocul fiecarei diagonale.
Def: Dreptunghiul reprezinta un caz particular al paralelogramului(deci are toate proprietatile paralelogramului si in plus are toate unghiurile drepte).
Teorema: Un paralelogram este dreptunghi daca si
numai daca diagonalele sale sunt congruente.
A B
*AB
|| CD *AB CD
O M
*BC || DA *AB DA
*Diagonalele se injumatatesc si sunt congruente :OAOB,OCOD
AC/2AOOC ;
●Perimetrul: PABCD=AB+BC+CD+DA=2AB + 2BC.
●Aria :AABCD=AB·AD (produsul dintre lungime si latime).
●**Def: Apotema unui poligon convex regulat reprezinta un segment de dreapta care este egal cu distanta de la centrul poligonului la una din laturi (deci perpendiculara dusa din centru la una din laturi). Daca "O" este centrul dreptunghiului atunci are doua apoteme , OM=AB/2 sI ON=BC/2.
Rombul
Def : Rombul reprezinta un paralelogram care are doua laturi consecutive congruente .
Teorema: Toate laturile rombului sunt congruente .
Teorema reciproca : Daca un patrulater convex are toate laturile congruente aunci el este romb .
Teorema: Intr-un romb diagonalele sunt perpendiculare intre ele si sunt bisectoarele unghiurilor lui ( diagonalele se injumatatesc ) .
Teorema reciproca : Daca un paralelogram are diagonalele perpendiculare , atunci el este romb .
A *AB || CD *AB BCCDDA
*BC || DA
*Diagonalele se injumatatesc si sunt perpendiculare :
d1OAOCd1 / 2 ;
OBODd2 / 2 ; d1 
d2
* <A = <C = unghiuri ascutite
Dd2 O B * <B = <D =
unghiuri obtuze
* [DB] =bisectoare pentru < ADC si < ABC .
M * [AC] =bisectoare pentru <DAB si < DCB .
Perimetrul : PABCD=AB+BC+CD+DA= 4 ∙ AB
C * Aria :AABCD=
4∙ AAOD=
=
=
*
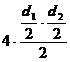Apotema OM= a =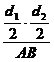 
Trapezul
Def : Trapezul reprezinta un patrulater care are doua laturi paralele si doua neparalele .
1) Trapezul oarecare are doua laturi paralele si doua neparalele .
Suma unghiurilor intr-un trapez este de 3600 . A B
Perimetrul este egal cu
suma lungimilor laturilor .
Aria este egala cu
produsul dintre linia mijlocie si inaltime . M N
Linia mijlocie este
egala cu semisuma bazelor ( linia mijlocie este o
dreapta paralela cu bazele si determina pe laturile care le intersecteaza
segmente congruente . CF D
pABCD= AB+BD+DC+CA ; S . UNGHIURILOR=<A+<B+<C+<D=3600
AABCD=
Daca [MN] este linie
mijlocie in trapezul ABCDAMMC si BN ND MN= 
AB // MN // CD .
Trapezul isoscel " Fig 1 " :
Teorema : Intr-un trapez isoscel unghiurile apropiate bazei sunt congruente (cele alaturate bazei mici sunt unghiuri ascutite , cele apropiate bazei mari sunt unghiuri obtuse ) .
Teorema : Daca un trapez este isoscel atunci , diagonalele lui sunt congruente .
Reciproca teoremei : Daca intr-un trapez diagonalele sunt congruente atunci acesta este trapez isoscel .
Fig . 1 A B A BFig . 2
D C DC
Trapezul dreptunghic " Fig . 2 " :
