
|
|
|
Functii diferentiabile
Fie Rn=R![]() R
R![]()
![]() R
R
Sa consideram acum o
functie f:D![]() Rn, unde D este o multime deschisa din Rn, n>1.
Atunci definitia1 a derivabilitatii se va scrie
Rn, unde D este o multime deschisa din Rn, n>1.
Atunci definitia1 a derivabilitatii se va scrie ![]()
![]() , unde f(x)-f(a)
, unde f(x)-f(a)![]() Rn si x-a
Rn si x-a![]() Rn .
Rn .
Observam ca definitia1 a derivabilitatii in punct nu mai are sens pentru
f:Rn![]() Rn, intrucat x-a este in acest caz un vector, iar impartirea
printr-un vector nu este definita.
Rn, intrucat x-a este in acest caz un vector, iar impartirea
printr-un vector nu este definita.
Insa, observam ca definitia5 a diferentiabilitatii functiei f in punctul a, care este echivalenta cu definitia1 a derivabilitatii in punct, se poate extinde, fara nici un fel de dificultate , la cazul functiilor de mai multe variabile reale.
In acest caz, avem urmatoarea definitie:
Definitia1
Fie D o multime deschisa din Rn(n≥1), F:D![]() Rm(m≥1) si a
Rm(m≥1) si a![]() D.
D.
a) Spunem ca functia F este diferentiabila
in punctul a![]() D daca (
D daca (![]() ) o aplicatie liniara T:Rn
) o aplicatie liniara T:Rn![]() Rm a.i.
Rm a.i.
(1) ![]()
![]() =0
=0
b) Spunem ca functia F
este diferentiabila pe D daca F este
diferentiabila in orice punct a![]() D.
D.
Vom nota
x-a=h, h![]() R, atunci forma (1) se mai poate scrie sub forma
echivalenta:
R, atunci forma (1) se mai poate scrie sub forma
echivalenta:
(1') ![]()
![]() =0
=0
De asemenea, daca notam cu ![]() (x)=
(x)=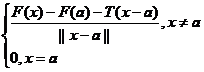
In acest caz, formula (1) se mai poate inca scrie si sub forma:
(2)F(x)=F(a)+T(x-a)+![]() (x)||x-a||, (
(x)||x-a||, (![]() ) x
) x![]() Dunde
Dunde ![]()
![]() (x)=
(x)=![]() (a)=0
(a)=0
Sau
(2') F(a+h)=F(a)+T(h)+![]() (a+h)||h||, (
(a+h)||h||, (![]() ) h
) h![]() Rna.i. a+h
Rna.i. a+h![]() D iar
D iar ![]()
![]() (a+h)=
(a+h)=![]() (a)=0
(a)=0
Definitia2
Daca D este un deschis din Rn si F:D![]() Rm este diferentiabila in punctual a
Rm este diferentiabila in punctual a![]() D, atunci aplicatia liniara T:Rn
D, atunci aplicatia liniara T:Rn![]() Rm se numeste diferentiala
functiei F in punctul a sau derivata Fréchet
a functiei F in punctual a.
Rm se numeste diferentiala
functiei F in punctul a sau derivata Fréchet
a functiei F in punctual a.
Vom notam: dF(a)
Observam ca h![]() Rn , df(a):Rn
Rn , df(a):Rn![]() Rm
Rm ![]() dF(a)
dF(a)![]() Rm
Rm
Atunci relatia (2') se scrie:
(2'') F(a+h)=F(a)+dF(a)(h)+||h||ˇ![]() (h), unde ||h|| se numeste norma elementului h din Rn si
(h), unde ||h|| se numeste norma elementului h din Rn si ![]() (h)
(h)![]() 0 (in Rm) , cand h
0 (in Rm) , cand h![]() 0 (in Rn).
0 (in Rn).
Teorema1
Fie D un deschis din Rn
(n≥1). Daca aplicatia F:D![]() Rm (m≥1) este diferentiabila in a
Rm (m≥1) este diferentiabila in a![]() D, atunc diferentiala sa in a este unica.
D, atunc diferentiala sa in a este unica.
Dem.
Daca aplicatia F:D![]() Rm (m≥1)este diferentiabila in a
Rm (m≥1)este diferentiabila in a![]() D rezulta conform definitiei (
D rezulta conform definitiei (![]() ) o aplicatie liniara T:Rn
) o aplicatie liniara T:Rn![]() Rma.i. (1)
Rma.i. (1) ![]()
![]() =0.
=0.
Pp ca pe langa aplicatia
liniara T care verefica relatia (1) ar
mai (![]() ) o aplicatie liniara S:Rn
) o aplicatie liniara S:Rn![]() Rm a.i.
Rm a.i.
(2) ![]()
![]() =0
=0
Vom nota x-a=h ![]() (2')
(2') ![]()
![]() =0
=0
Pentru ![]() h
h![]() are loc:
are loc:
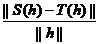 ≤
≤ ![]() ≤
≤
≤![]() +
+![]()
Facand h![]() 0
0 ![]()
![]()
![]() =0
=0
![]()
![]() =0
=0
![]() (3)
(3) ![]()
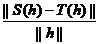 =0
=0
Observam ca: (![]() ) y
) y![]() Rn , daca t>0 si t
Rn , daca t>0 si t![]() 0 in R
0 in R ![]() ty
ty![]() 0 in Rn.
0 in Rn.
Consideram y arbritar din
Rn cu y![]() 0 si h=ty din relatia (3)
0 si h=ty din relatia (3)![]()
0=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ||S(y)-T(y)||=0, (
||S(y)-T(y)||=0, (![]() ) y
) y![]() Rn , adica S(y)=T(y) pentru
Rn , adica S(y)=T(y) pentru ![]() y
y![]() Rn de unde S=T.
Rn de unde S=T.
In particular pentru y=0 ![]() S(0)=T(0)=0
S(0)=T(0)=0 ![]() S(y)=T(y), pentru y
S(y)=T(y), pentru y![]() Rn
Rn
In continuare vom analiza cateva proprietati generale ale functiilor diferentiabile.
Teorema2
Fie D un deschis din Rn .Daca F:D![]() Rm este diferentiabila in a
Rm este diferentiabila in a![]() D atunci F este continua in a.
D atunci F este continua in a.
Dem.
Cum F este
diferentiabila in a, (![]() ) o aplicatie liniara T:Rn
) o aplicatie liniara T:Rn![]() Rm si o aplicatie
Rm si o aplicatie ![]() :D
:D![]() Rm cu
Rm cu ![]() a.i.
F(x)=F(a)+T(x-a)+
a.i.
F(x)=F(a)+T(x-a)+![]() (x)||x-a||, (
(x)||x-a||, (![]() )x
)x![]() D
D
Teorema
Daca T:Rn![]() Rm este un operator liniar, atunci T
este operatot continuu.
Rm este un operator liniar, atunci T
este operatot continuu.
T=operator liniar continuu pe Rn si, deci in a
![]() =continua in a
=continua in a ![]() F este continua in a
F este continua in a
Teorema3
Fie D un deschis din Rn , n≥1
si F:D![]() Rm , m≥1, in care F=(f1,f2,..,fm) cu fi:D
Rm , m≥1, in care F=(f1,f2,..,fm) cu fi:D![]() R, i=
R, i=![]() .Functia F este diferentiabila in a
.Functia F este diferentiabila in a![]() D
D![]() functiile fi sunt diferentiabile in a si in acest
caz
functiile fi sunt diferentiabile in a si in acest
caz
dF(a)=(df1(a),df2(a),..,dfm(a)), adica diferentiala lui f in a are drept componente diferentiale dfi(a) ca aplicatii liniare de la Rn la R.
dem.
Daca F
este diferentiabila in a, atunci (![]() ) o aplicatie liniara T:Rn
) o aplicatie liniara T:Rn![]() Rm cu componentele (t1,t2,.,tm)
si o functie
Rm cu componentele (t1,t2,.,tm)
si o functie ![]() :D
:D![]() Rm cu componentele (
Rm cu componentele (![]() ,
,![]() ,..,
,..,![]() ) in care
) in care ![]()
![]() , a.i.(1) F(x)=F(a)+T(x-a)+
, a.i.(1) F(x)=F(a)+T(x-a)+![]() ||x-a|| ,
||x-a|| , ![]() x
x![]() D
D
Daca scriem pe componente vom obtine:
(2) 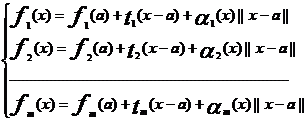 ,
,![]() x
x![]() D, ti:Rn
D, ti:Rn ![]() R(aplicatii liniare)
R(aplicatii liniare)
![]()
![]() ,
,![]() i=
i=![]()
![]() formula 9 exprima tocmai conditia de
diferentiabilitate a functiilor fi in a si in plus cum T=(t1,t2,...,tm)
formula 9 exprima tocmai conditia de
diferentiabilitate a functiilor fi in a si in plus cum T=(t1,t2,...,tm)
![]() dF(a)=(df1(a),df2(a),..,dfm(a)).
dF(a)=(df1(a),df2(a),..,dfm(a)).
Teorema4
Daca F:Rn![]() Rm este o functie constanta, atunci este
diferentiabila pe Rn iar in
Rm este o functie constanta, atunci este
diferentiabila pe Rn iar in ![]() a
a![]() Rn are loc: dF(a)=0
Rn are loc: dF(a)=0
Dem.
Intrucat functia F este constanta ![]() (
(![]() ) c
) c![]() Rn a.i.F(x)=c,
Rn a.i.F(x)=c, ![]() x
x![]() Rn
Rn
Atunci ![]()
![]()
![]()
![]() =0
=0 ![]() F este
diferentiabila
F este
diferentiabila
dF(a)=0 ![]() T(h)=0
T(h)=0
Teorema5
Daca T:Rn![]() Rm , (n≥1,m≥1) este o
aplicatie liniara, atunci dT(a)=T,
Rm , (n≥1,m≥1) este o
aplicatie liniara, atunci dT(a)=T, ![]() a
a![]() Rn .
Rn .
Dem.
Cum T este aplicatie liniara ![]() T(a+h)=T(a)+T(h),
T(a+h)=T(a)+T(h), ![]() a,h
a,h![]() Rn
Rn
Atunci ![]()
![]() =
=![]()
![]() =0
=0 ![]() T diferentiabila in a
T diferentiabila in a ![]() dT(a)=T.
dT(a)=T.
Teorema6
Daca F,G:D![]() Rm, unde D este un deschis din Rn, sunt
diferentiabile in a si
Rm, unde D este un deschis din Rn, sunt
diferentiabile in a si ![]()
![]() R, atunci F+G si
R, atunci F+G si ![]() F sunt diferentiabile in a si
F sunt diferentiabile in a si
a) d(F+G)(a)=dF(a)+dG(a)
b) d(![]() F)(a)=
F)(a)=![]() dF(a)
dF(a)
dem.
a) fie T=dF(a) S=dG(a)
stim ca: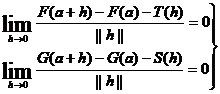
![]()
![]()
![]()
![]() +
+![]()
![]() =0
=0 ![]() F+G diferentiabila in
a
F+G diferentiabila in
a ![]() d(F+G)(a)=T+S=dF(a)+dG(a).
d(F+G)(a)=T+S=dF(a)+dG(a).
b) d(![]() F)(a)=
F)(a)=![]() dF(a)
dF(a)
notam T=![]() dF(a)
dF(a)
F este
diferentiabila ![]()
![]()
![]()
Atunci ![]()
![]() =
=![]()
![]()
![]()
![]()
![]() F este diferentiabila in a
F este diferentiabila in a ![]() d(
d(![]() F)(a)=
F)(a)=![]() dF(a)
dF(a)
Teorema7
Fie D un deschis din Rn , F:D![]() R si G:D
R si G:D![]() Rm doua functii diferentiabile in a
Rm doua functii diferentiabile in a![]() D.Atunci functia F:D
D.Atunci functia F:D![]() Rn este diferentiabila in a si are loc
Rn este diferentiabila in a si are loc
d(FG)(a)=F(a)dG(a)+dF(a)G(a)
dem.
Cum F si G sunt diferentiabile in a ![]() (
(![]() ) o functie
) o functie ![]() :D
:D![]() R cu
R cu ![]()
![]() (x)=0 a. i. F(x)=F(a)+dF(a)(x-a)+||x-a||
(x)=0 a. i. F(x)=F(a)+dF(a)(x-a)+||x-a||![]() (x),
(x), ![]() x
x![]() D si (
D si (![]() ) o functie
) o functie ![]() :D
:D![]() Rm cu
Rm cu ![]() a.i.
G(x)=G(a)+dG(a)(x-a)+||x-a||
a.i.
G(x)=G(a)+dG(a)(x-a)+||x-a||![]() (x),
(x), ![]() x
x![]() D.
D.
Daca h![]() Rn
Rn ![]() (dF(a)G(a))h=dF(a)(h)G(a) in care dF(a)(h)
(dF(a)G(a))h=dF(a)(h)G(a) in care dF(a)(h)![]() R si G(a)
R si G(a)![]() Rm , dF(a)G(a):Rn
Rm , dF(a)G(a):Rn![]() Rm (operator liniar)
Rm (operator liniar)
(FG)(x)=F(x)ˇG(x)=[F(a)+dF(a)(x-a)+||x-a||![]() ]ˇ[G(a)+dG(a)(x-a)+||x-a||
]ˇ[G(a)+dG(a)(x-a)+||x-a||![]() ]=(FG)(a)+(x-a)[F(a)dG(a)+dF(a)G(a)]+||x-a||
]=(FG)(a)+(x-a)[F(a)dG(a)+dF(a)G(a)]+||x-a||![]() G(a)+||x-a||
G(a)+||x-a||![]() dG(a)(x-a)+||x-a||2
dG(a)(x-a)+||x-a||2 ![]()
![]() +||x-a||F(a)
+||x-a||F(a)![]() +dF(a)(x-a)
+dF(a)(x-a)![]() ||x-a||+dF(a)(x-a)dG(a)(x-a)
||x-a||+dF(a)(x-a)dG(a)(x-a)
Notam ![]() =
=![]() G(a)+
G(a)+![]() dG(a)(x-a)+||x-a||
dG(a)(x-a)+||x-a||![]()
![]() +F(a)
+F(a)![]() +dF(a)(x-a)
+dF(a)(x-a)![]() +
+![]() , x≠a.
, x≠a.
F(a)dG(a)+dF(a)G(a):Rn![]() Rn (operator liniar)
Rn (operator liniar) ![]()
![]()
![]() d(FG)(a)=dF(a)G(a)+F(a)dG(a).
d(FG)(a)=dF(a)G(a)+F(a)dG(a).