Spatiu vectorial in raport cu un corp K

Spatiu vectorial in raport cu un corp K

Definitia 1.1. Se numeste spatiu vectorial (liniar) in raport cu corpul K, multimea X nevida, inzestrata cu o lege de compozitie interna (notata aditiv si numita adunare):

"+" : X X X,

o lege de compozitie externa (notata multiplicativ si numita inmultire cu scalar):

" " : K X X,

care au urmatoarele proprietati:

(i). (x + y) + z = x + (y + z), ( ) x, y, z I X (asociativitate);

(ii). ( ) in X un element, notat 0, numit element neutru, astfel ca

x + 0 = 0 + x = x, ( ) xIX

(iii). ( ) x I X, ( ) in X un element, notat - x, numit opusul elementului x, astfel ca: x + (- x) = (- x) + x = 0;

(iv). x + y = y + x, ( ) x, y I X (comutativitate);

(v). a b x = a x + b x, ( a bIK, xIX

(vi). a ( x + y) = a x + a y, ( aIK, x, yIX

(vii). a b x = a b x), ( a bIK, xIX

(viii). Daca 1I K atunci 1 x = x, ( ) xI X.

Elementele spatiului vectorial X le vom numi vectori, iar elementele corpului K le vom numi scalari. Elementul 0 se mai numeste elementul nul al spatiului X.

Corpul K este unul din corpurile R al numerelor reale sau corpul C al numerelor complexe; daca K s R atunci X se numeste spatiu vectorial real, iar daca K s C spatiul X se numeste spatiu vectorial complex.

Exemple: 1). Produsul cartezian Kⁿ = K K K, adica multimea:

Kⁿ

formeaza o structura de spatiu vectorial peste corpul K, daca definim operatiile de adunare si inmultire cu scalari astfel:

(x₁, x₂, ..,x_n) + (y_1, y₂, .,y_n) = (x₁ + y₁, x₂ + y₂,., x_n + y_n)

si

a (x₁, x₂, .x_n) = (ax₁, ax₂, ., ax_n)

Vectorul nul este in acest caz vectorul 0 = (0, 0, .,0), iar opusul vectorului

x = (x_1, x₂, .x_n) este vectorul -x = (-x_1, -x₂, .-x_n).

2). Multimea polinoamelor de o nedeterminata, de grad cel mult n (nIN), cu coeficienti intr-un corp K, in raport cu operatiile de adunare a polinoamelor si de inmultire a polinoamelor cu un element din corpul K.

Cazuri particulare:

Rⁿ

Cⁿ

3). Multimea sirurilor x = (x_n)_nIN de numere reale sau complexe, care satisfac conditia de marginire:

x_n a(x), ( ) nIN

a(x) fiind un numar pozitiv care depinde de x, cu legile de compozitie astfel definite:

(x_n)_nIN + (y_n)_nIN = (x_n + y_n)_nIN

a (x_n)_nIN = a (x_n)_nIN aIK

(4). Multimea C₀[a,b] = a functiilor continue pe intervalul inchis [a,b] in raport cu operatiile:

(f + g)(t) = f(t) + g(t), ( ) tI[a,b],

(a f )(t) = a f(t) , ( aIR, tI[a,b].

5). Multimea M_m,n(K) a matricelor cu m linii si n coloane cu elemente numere reale (sau complexe) formeaza un spatiu vectorial peste corpul R (sau C), in raport cu operatiile de adunare a matricelor de acelasi tip si de inmultire a matricelor cu un scalar.

Daca A,BM_m,n(K), A = , B = se defineste suma celor doua matrice ca fiind matricea

S = A+B, SM_m,n(K), S = , s_ij = a_ij + b_ij , ,

iar inmultirea cu scalari a unei matrice este tot o matrice definita astfel:ESV

(α,A)αA, αAM_m,n(K),

.

6). Spatiul vectorial al vectorilor liberi.

Notam prin E₃ spatiul geometric punctual (adica multimea punctelor din spatiul ambiant).

Definitia 1.2. O pereche E₃ E₃ se numeste segment orientat din E₃, de origine si extremitate . Acesta se noteaza . Lungimea segmentului orientat se numeste modulul acestuia si se noteaza ||.

Definitia 1.3. Doua segmente orientate si se numesc echipolente daca patrulaterul este paralelogram. Se noteaza ~.

Relatia de echipolenta definita mai sus are urmatoarele proprietati, a caror justificare este imediata:

a). ~;

b). ~~;

c). ~ si ~ ~;

deci relatia ~" este o relatie de echivalenta in multimea segmentelor orientate.

Definitia 1.4. O clasa de echivalenta in raport cu relatia de echipolenta in multimea segmentelor orientate din E₃ se numeste vector liber.

Deci un vector liber poate fi considerat ca fiind multimea segmentelor orientate echipolente cu un vector dat.

Deoarece doua segmente orientate echipolente au module egale, aceeasi directie (adica dreptele care unesc extremitatilelor au aceeasi directie) si aceeasi orientare, rezulta ca modulul, directie si sensul, comune tuturor segmentelor orientate dintr-o clasa de ecxhivalenta, sunt elemente ce caracterizeaza vectorii liberi.

Vom nota vectorii liberi prin , multimea vectorilor liberi prin V₃ (V₃ = S₃/~), iar modulul vectorului prin ||||.

Constructia notiunii de vector liber este sugerata in figura urmatoare:

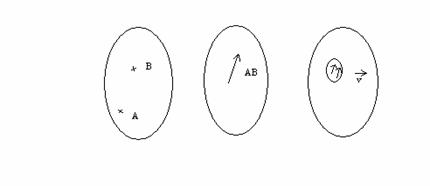
E₃ S₃ V₃

Propozitia 1. Orice vector liber admite reprezentare unica printr-un segment orientat in orice punct din spatiul E₃.

Demonstratie. Fie vectorul si un punct E₃. Notam cu sfera de centru si de raza ||||. Aceasta este intersectata de dreapta ce trece prin si are directia lui , in doua puncte si . Unul singur dintre segmentele orientate si are sensul lui si acesta este cel cautat.

Doi vectori liberi sunt egali daca si numai daca au module egale, aceeasi directie si orientare.

Definitia 1.5. Se numeste adunare a vectorilor liberi legea de compunere V₃ V₃ V₃, care asociaza vectorilor si , vectorul definit prin regula triunghiului sau regula paralelogramului, reprezentate in continuare:

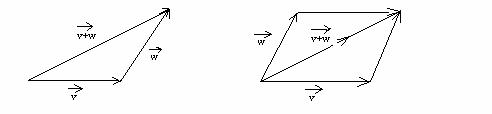
Propozitia 2. Multimea V₃ a vectorilor liberi poseda o structura de grup abelian in raport cu adunarea.

Demonstratia este imediata.

Definitia 1.6. Se numeste amplificatul vectorului liber prin scalarul , vectorul definit astfel:

a). ;

b). pentru orientarile vectorilor si coincid iar pentru

acestea sunt opuse;

c). directia lui coincide cu cea a lui .

Se demonstreza cu usurinta urmatorul rezultat:

Propozitia 3. Pentru orice V₃ si avem:

a). ;        

b). ;

c). ;

d).

Din propozitiile 1 si 2 rezulta urmatorul rezultat

Teorema 1. Multimea V₃ a vectorilor liberi poseda o structura de spatiu vectorial peste corpul numerelor reale in raport cu operatiie de adunare si amplificare a vectorilor cu scalari.

Observatie. Notand cu E₂ planul punctual, o constructie identica cu cea de mai sus ne permite sa obtinem spatiul V₂ al vectorilor liberi din plan.

Operatii cu vectori

1.     Produsul scalar

Se numeste produs scalar din V₃ aplicatia:

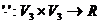
definita prin:

.

Daca si atunci .

2.     Produsul vectorial

Dati fiind vectorii si se numeste produs vectorial al lor, vectorul:

.

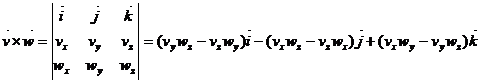3.     Produsul mixt

Dati fiind vectorii , si se numeste produs mixt scalarul:

.

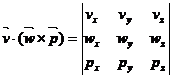4.     Dublul produs vectorial

Se numeste dublu produs vectorial vectorul .

Reguli de calcul intr-un spatiu vectorial:

(i). 0 x = 0, a 0 = 0, ( aIK, xIX

(ii). a x = 0 T a = 0 sau x = 0;

(iii). (- a x a x a (-x) = -a x aIK, xIX

Definitia 1.2. Se numeste produs scalar pe spatiul vectorial X peste corpul K

(= R, sau C), o functie ps : X X K, cu urmatoarele proprietati:

(i). ps(x, y) = ;

(ii). ps(a x b y, z a ps(x, z) +b ps(y, z);

(iii). ps(x, x) 0; ps(x, x) = 0 x = 0.

Valoarea reala x = se numeste lungimea sau norma vectorului x.

Definitia 1.3. Un spatiu vectorial (peste corpul K) inzestrat cu un produs scalar se numeste spatiu vectorial euclidian (daca K = R), sau spatiu unitar (daca K = C).

Exemplu. Spatiul euclidian al vectorilor liberi.

Produsul scalar al vectorilor din V₃ este aplicatia V₃ V₃ R, definita prin .                  

Dependenta si independenta liniara

Fie X un spatiu vectorial peste corpul K.

i =1,2,.,m; j =1,2,.,r_i Vectorul xX este o combinatie liniara de vectorii x_i (i=1, 2, ., m) din X, daca el se poate reprezenta astfel:

.

Observatii (i). Vectorul nul este combinatie liniara de orice familie de vectori.

(ii). Daca vectorul x este o combinatie liniara de vectorii x_i (i=1, 2, ., m) si fiecare vector x_i este o combinatie liniara de vectorii y_ij (i =1,2,.,m; j =1,2,.,r_i), atunci x este o combinatie liniara de vectorii y_ij (i =1,2,.,m; j =1,2,.,r_i).

Intr-adevar:

;

, j =1,2,.,r_i; i =1,2,.,m,

prin urmare:

, i =1,2,.,m; j =1,2,.,r_i .

Definitia . Vectorii I - familie de indici, se numesc liniar independenti, daca ; in caz contrar vectorii se numesc liniar dependenti, adica vectorii sunt liniar dependenti, daca exista cel putin un , astfel ca .

Teorema . Un sistem de vectori este liniar dependent daca si numai daca exista cel putin un indice astfel ca x_j sa fie o combinatie liniara de vectorii .

Demonstratie. Fie ; luand rezulta , deci vectorii sunt liniar dependenti.

Reciproc, fie ; inmultim relatia precedenta cu si obtinem

,

unde

.

Teorema . Un sistem de vectori este liniar independent daca si numai daca orice vector poate fi scris in cel mult un mod ca o combinatie liniara de vectorii , adica daca si numai daca din combinatia liniara:

,

rezulta ca scalarii sunt unic determinati de x.

Demonstratie. Suficienta. Presupunem ca in relatia: ,

scalarii sunt unic determinati de x. Luam, in particular, x = 0, caz in care rezulta:

;

deoarece aceasta relatie are loc numai pentru scalarii , vectorii sunt liniar independenti.

Necesitatea. Presupunem ca vectorii sunt liniar independenti; atunci

.

Definitia . O multime se numeste liniar independenta, daca orice parte finita a ei este formata din vectori liniari independenti.

Definitia . O multime liniar independenta maximala de vectori din A se numeste baza a multimii A.

Definitia . Daca multimea A (in particular spatiul X) are o baza finita atunci se spune ca A (respectiv X) are dimensiune finita; in caz contrar se spune ca A (respective X) are dimensiune infinita.

Teorema . Daca vectorii x_i (i =1,2,,m) constituie o baza a multimii A atunci reprezentarea unui vector xA ca o combinatie liniara de vectorii x_i (i =1,2,,m) este unica.

Demonstratie. Presupunerea ca ar admite doua reprezentari este contradictorie.

x

Definitia . Daca x_i (i =1,2,,m) este o baza, scalarii pentru care are loc relatia , determinati in mod unic de vectorul x, se numesc coordonatele vectorului x in baza x_i (i =1,2,,m).

Subspatii vectoriale

Definitia . Fie X un spatiu vectorial si X₀ X. Daca X₀ este parte stabila fata de adunarea vectorilor (adica ) si fata de inmultirea cu scalari a vectorilor (adica ) atunci X₀ se numeste subspatiu vectorial al lui X.

Teorema . Orice intersectie de subspatii vectoriale ale lui X este un subspatiu vectorial al lui X.

Demonstratie. Fie X_i X subspatii vectoriale ale lui X, - familie de indici.

Notam: ; .

.

Analog , prin urmare X₀ este subspatiu vectorial al lui X.

Definitia . Fie o parte a lui X. Se numeste subspatiu vectorial generat de A, sau acoperirea liniara a lui A, cel mai mic subspatiu vectorial cae include pe A, adica intersectia tuturor subspatiilor vectoriale care include pe A.

Notam:

- subspatiul vectorial generat de A, adica X_i - subspatiu vectorial;

- multimea tuturor combinatiilor liniare de elemente din A, adica:

.

Teorema . .

Demonstratie. .

Orice combinatie liniara de elemente din A apartine oricarui subspatiu care include pe A, deci .

In cele ce urmeaza ne vom situa in spatiul euclidian Rⁿ in care produsul scalar este definit astfel:

ps : Rⁿ Rⁿ R

ps(x, y) = , x = (x₁, x₂,.,x_n), y = (y₁, y₂, .,y_n).

Vom nota in continuare: ps(x, y) = <x, y>= xy.

Norma vectorului x este x = = .

Spatiul Rⁿ (Spatiul cu n dimensiuni). Structura algebrica

Produsul cartezian Rⁿ = R R R, adica multimea:

Rⁿ

formeaza o structura de spatiu vectorial peste corpul R, daca definim operatiile de adunare si inmultire cu scalari astfel:

(x₁, x₂, ..,x_n) + (y_1, y₂, .,y_n) = (x₁ + y₁, x₂ + y₂,., x_n + y_n),

unde

x =(x₁, x₂,.,x_n), y = (y₁, y₂, .,y_n), x, y Rⁿ

si

a (x₁, x₂, .x_n) = (ax₁, ax₂, ., ax_n),

unde

x =(x₁, x₂,.,x_n)Rⁿ , α R .

Cazuri particulare

(i). n=1; R¹ este multimea punctelor de pe dreapta reala R;

(ii). n=2; R²=este multimea punctelor din plan;

(iii). n=3; R³=este multimea punctelor din spatiu.

Definitia . O aplicatie , se numeste norma pe Rⁿ , daca satisface proprietatile:

(i). ;

(ii). , ();

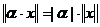(iii). , (.

Teorema . (a). Aplicatia ps : Rⁿ Rⁿ R, definita prin:

ps(x, y) = , x = (x₁, x₂,.,x_n), y = (y₁, y₂, .,y_n),

este un produs scalar pe Rⁿ .

(b). Aplicata definita prin:

x = = , x,

este o norma pe Rⁿ .

Demonstratie. (a). Proprietatile (i)-(iv) ale produsului scalar se verifica imediat.

(b). De asemenea proprietatile (i)-(ii) ale normei rezulta imediat din proprietatile produsului scalar. Pentru demonstra cea de a treia proprietate de la norma, demonstram in prealabil doua inegalitati si anume:

(α). ;

(β). ; (inegalitatea lui Schwarz);

(α). Din rezulta:

.

(β). Daca atunci sau deci , sau deci ; in ambele cazuri ps(x, y) = 0, deci inegalitatea este demonstrata.

Daca atunci , si .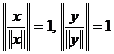

Notam si rezulta:

,

adica

deci

.

Folosind inegalitatea (β) rezulta imediat inegalitatea riunghiului:

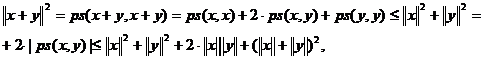
de unde:

.

Definitia . Se numeste distanta (metrica) pe Rⁿ, o aplicatie , care satisface proprietatile:

(i). ;

(ii). ;

(iii). ; (inegalitatea triunghiului).

Teorema . Aplicatia , definita prin:

,

este o distanta (metrica) pe Rⁿ.

Definitia . (i). Un spatiu vectorial pe care s-a definit o norma care satisface proprietatile (i), (ii), (iii) (de la norma) se numeste spatiu vectorial normat, sau mai scurt, spatiu normat.

(ii). O multime X inzestrata cu o metrica , deci perechea , se numeste spatiu metric.

Observatie. Un spatiu normat este in acelasi timp si spatiu metric, cu metrica indusa de norma; exista insa si spatii metrice in care distanta (metrica) nu poate fi dedusa dintr-o norma.

Teorema . Orice sistem de n vectori x₁, x₂, ,x_n Rⁿ ; x_i = ,

i =1,2,.,n, cu proprietatea ca:

,

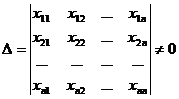formeaza o baza a lui Rⁿ.

Demonstratie. Vectorii x₁, x₂, ,x_n Rⁿ sunt liniar independenti deoarece

.

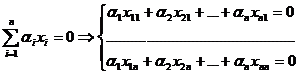Sistemul de ecuatii liniare omogene (deoarece determinantul asociat matricei coeficientilor este nenul) are solutia unica .

Deoarece rezulta de asemenea ca orice vector x Rⁿ se scrie, in mod unic, sub forma .

Observatie. Sistemul de vectori Rⁿ unde:

e₁ (1,0,,0)

e₂ (0,1,,0)

e_n (0,0,,1)

formeaza o baza a spatiului Rⁿ , numita baza canonica.

Operatii cu matrice partitionate

Ne situam de aceasta data in spatiul vectorial M_m,n(K) a matricelor cu m linii si n coloane peste corpul R (sau C).

Deseori este util sa se efectueze operatii cu matrice partitionate. Vom vedea avantajul partitionarii in special in cazul inversarii unei matrice prin partitionare, unde, in loc de a calcula inversa unei matrice de dimensiuni relativ mari, este suficient sa calculam inversele a doua matrice de dimensiuni mai mici.

Definitia . Se numeste partitionare a unei matrice A o impartire a matricei A in submatrice prin drepte orizontale si verticale.

Exemplu: Matricea AM_m,n(K) poate fi partitionata in submatricele:

A₁₁M_r,s(K), A₁₂M_r,n-s(K), A₂₁M_m-r,s(K), A₂₂M_m-r,n-s(K);

A'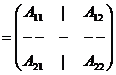

unde

A₁₁ =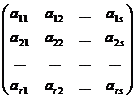 , A₁₂ = ,

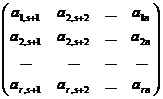A₂₁ =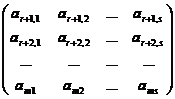 , A₂₂ = .

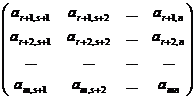Adunarea prin partitionare a doua matrice de acelasi tip (de aceeasi dimensiune) si la fel partitionate, se realizeaza in mod obisnuit, interpretand submatricele ca si cum ar fi elemente ale matricei.

Fie matricea BM_m,n(K), de acelasi tip si partitionata la fel ca matricea A:

B.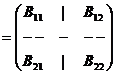

Atunci suma celor doua matrice este matricea SM_m,n(K),

S = A + B ,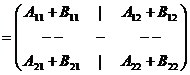

S fiind partitionata analog cu matricele A si B.

Realizarea operatiei de inmultire a matricelor presupune partitionarea celor doua matrice conforma cerintelor inmultirii, adica diviziunile verticale ale primei matrices a fie aceleasi cu diviziunile orizontale ale celei de a doua matrice.

Se dau matricele AM_m,n(K), BM_np(K):

m, cu ;

n, cu ;

atunci:

.

Ne propunem acum sa determinam inversa unei matrice prin partitionare.

Fie AM_,n(R),

A₁₁M_m(K), A₁₂M_m,,n-m(K), A₂₁M_n,-m,m(K), A₂₂M_n-m,n-m(K);

A.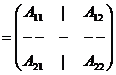

Presupunem ca si determinam inversa A^-1, necunoscuta, partitionata la fel ca matricea A:

A^-1 ,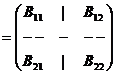

din conditia .

Facand inmultirea prin partitionare rezulta:

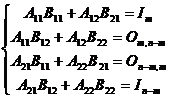
de unde rezulta:

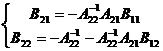
si mai departe

.

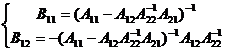
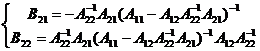Cazuri particulare

(i). Calculati inversa matricei:

,

unde , , , si α - aA^-1b0.

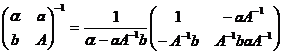
(ii). Calculati inversa matricei:

,

unde , , , si α - bA^-1a0.

.

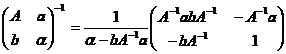Structura topologica a spatiului Rⁿ.

Definitia . Fie n intervale pe dreapta reala I₁, I₂,, I_n R; produsul lor cartezian se numeste interval n - dimensional;

.

Intervalele M_m,n(K)se numesc laturile intervalului n - dimensional.

Definitia . (i). O multime DR este deschisa daca, sau este vida, sau daca nu este vida, atunci pentru orice xD exista un r > 0, astfel incat .

(ii). Spunem ca V este o vecinatate a punctului xR, daca exista multimea deschisa D astfel incat x. Notam cu V(x) multimea vecinatatilor lui x.

(iii). Fie AR si x R. Spunem ca x este un punct interior al multimii A, daca A. Multimea 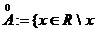- este punct interior al lui A}se numeste interiorul multimii A.

(iv). O multime AR se numeste inchisa daca complementara sa este deschisa.

(v). Fie AR si x R. Spunem ca x este punct aderent (respectiv punct de acumulare) al multimii A, daca pentru orice VV(x), are loc:

, (respectiv ).

Multimile:

este punct aderent al multimii A},

respectiv

este punct de acumulare al multimii A},

se numesc aderenta sau inchiderea multimii A, respectiv multimea derivata a lui A.

Daca toate intervalele I₁, I₂,, I_n sunt deschise, atunci I se numeste interval

n dimensional deschis.

Daca toate intervalele I₁, I₂,, I_n sunt inchise, atunci I se numeste interval

n dimensional inchis.

Daca toate intervalele I₁, I₂,, I_n sunt marginite, atunci I se numeste interval

n dimensional marginit.

Exemple de intervale in Rⁿ

In figura 1 sunt prezentate exemple de intervale din R², in cazul a). deschise (linia intrerupta simbolizeaza faptul ca extremitatea respectiva nu apartine intervalului), b). Inchise (linia continua simbolizeaza faptul ca extremitatea respectiva apartine intervalului), c). marginite.

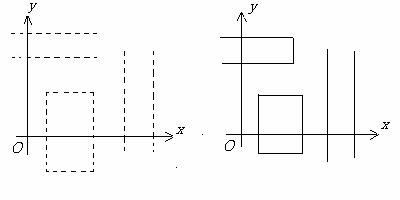
a). b).

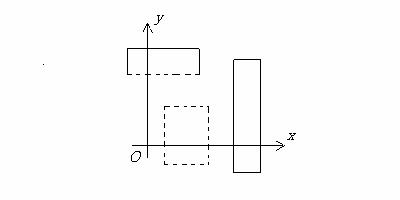
c).

Figura 1.

Definitia . (i). Fie aRⁿ si r > 0. Se numeste sfera deschisa), cu centrul in a si de raza r, multimea:

.

(ii). Multimea:

se numeste sfera (inchisa), cu centrul in a si de raza r.

Cazuri particulare

(i). n = 1, R¹ = R , deci sfera deschisa este un interval deschis cu centrul in a;

(ii). n = 2, a = (a₁, a₂)R² ,

este cercul de centrul a si raza r.

In general cand vorbim de sfera subintelegem sfera deschisa.

Prezentam in continuare un rezultat care exprima faptul ca in Rⁿ sfera de centrul a si raza r joaca acelasi rol ca intervalul n - dimensional care contine pe a.

Teorema . Orice sfera cu centrul in a contine un interval n - dimensional care contine pe a si reciproc, orice interval care contine pe a contine o sfera cu centrul in a.

Demonstratie. Fie o sfera cu centrul in a si de raza r.

,

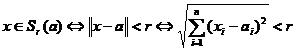unde x = (x₁, x₂, .,x_n) si a = (a₁, a₂, .,a_n).

Consideram intervalele unidimensionale:

si intervalul n - dimensional , ; .

Aratam ca ;

.

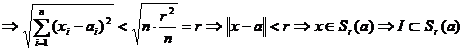Reciproc, fie , interval n - dimensional care contine pe a; intervalul I contine un interval n - dimensional cu centrul in a si cu intervalele J₁, J₂,.,J_n de aceeasi lungime:

.

Aratam ca , de unde va rezulta ca ;

.

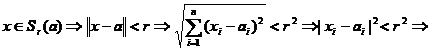
Concluzii cu privire la unele elemente de topologie in Rⁿ:

(i). O vecinatate a unui punct aRⁿ este orice multime care contine o sfera cu centrul in a.

(ii). O multime este vecinatate a unui punct aRⁿ , daca si numai daca exista un interval n -dimensional I, astfel ca a.

(iii). O multime ARⁿ este marginita, daca exista o sfera, ( care poate fi presupusa cu centru in origine), care contine pe A.

(iv). Multimile marginite si inchise din Rⁿ se numesc multimi compacte.

Aplicatii.

1.     Sa se studieze dependenta liniara pentru sistemele de vectori:

a). v₁ = (2, 1, 3, 1), v₂ = (1, 2, 0, 1), v₃ = (-1, 1, -3, 0) in R⁴;

b). v₁ = 8-t+7t², v₂ = 2-t+3t², v₃ = 1+t-3t² in P₂(t);

c). A₁ = , A₂ = , A₃ = in M_2,2(R).

2. Sa se determine care dintre polinoamele t² si t-1 apartin spatiului generat de

3.     In R⁴ se dau vectorii v₁ = (1, 1, 2, 1), v₂ = (1, -1, 0, 1), v₃ = (0, 0, -1, 1),

v₄ = (1, 2, 2, 0). Sa se arate ca acestia formeaza o baza. Se cer coordonatele vectorului v = (1, 1, 1, 1) in aceasta baza.

4.     In R⁵ sa se determine o baza a subspatiului vectorial generat de vectorii

v₁ = (1, 2, -4, 3, 1), v₂ = (2, 5, -3, 4, 8), v₃ = (6, 17, -7, 10, 22),

v₄ = (1, 3, -3, 2, 0).

5.     Se dau vectorii a₁ = (1, 0, 0), a₂ = (2, 1, 0), a₃ = (-3, 2, 1) si a = -8a₁+4a₂-a₃, precum si vectorii b₁ = a₁ + a₂ +a₃, b₂ = a₁ + a₂ - a₃, b₃ = a₁ -a₂ + a₃. Sa se calculeze coordonatele vectorului a in baza .

6.     Sa se determine vectorul normat v din R⁴ (de modul egal cu unitatea), ortogonal vectorilor v₁ = (1, 1, 1, 1), v₂ = (1, -1, -1, 1), v₃ = (2, 1, 1, 3).

7.     Sa se arate ca functia prin

<x, y> = 3x₁y₁-x₁y₂-x₂y₁+2x₁y₂ , x = (x₁, x₂), y = (y₁, y₂),

este un produs scalar.

8.     Sa se arate ca urmatoarele multimi sunt subspatii vectoriale ale spatiilor vectoriale indicate:

a). ;

b). ;

c). D = , F fiind multimea functiilor reale de variabila reala, diferentiabile.

9. Sa se determine λ, μastfel ca matricele

sa fie liniar independente.

10.  Sa se construiasca o baza ortonormata (adica o baza in care toti vectorii au modul egal cu unitatea si sunt doi cate doi ortogonali) a spatiului R⁴ , presupunand ca doi vectori ai bazei sunt v₁ = ( si

v₂ = (.