
|
|
|
Reprezentarea grafica a rezultatelor masurarilor reale poate lua diverse forme, curba distributiei putand fi unimodala sau multimodala, aplatizata sau inalta, simetrica sau asimetrica. In statistica exista insa un tip special de distributie, numita "distributie normala", care corespunde reprezentarii grafice a unei caracteristici pentru care exista un mare numar de masurari, tinzand spre infinit. Acest tip de distributie este numita "teoretica" pentru ca nu este rezultatul unui proces real de masurare ci reprezinta un model teoretic. Conceptul de "curba normala" (expresia grafica a "distributiei normale") se refera la acest tip de distributie teoretica si are cateva proprietati caracteristice:
1. Are forma de "clopot". Cea mai mare parte a valorilor se concentreaza in zona centrala (medie)
2. Este perfect simetrica pe ambele laturi ale sale
3. Linia curbei se apropie la infinit de axa X, fara a o atinge vreodata
4. In conformitate cu proprietatea 2, de fiecare parte a mediei se afla exact jumatate dintre valorile distributiei
Exemple de curbe normale
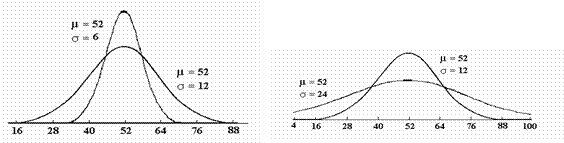
Imaginea de mai sus ilustreaza diferite variante ale familiei de curbe normale, care respecta, fiecare dintre ele, conditiile de mai sus, chiar daca au medii si abateri standard diferite.
Curba normala in care valorile sunt exprimate in scoruri z se numeste curba normala standardizata. Ea are toate proprietatile enuntate mai sus, avand insa si parametrii oricarei distributii z: m=0 si s=1. Valoarea 0 pentru medie a fost aleasa conventional pentru ca astfel distributia este simetrica in jurul lui 0.

Curba normala standardizata are cateva caracteristici care sunt figurate in imaginea de mai sus si pe care este important sa le retinem:
Aproximativ 34% dintre scorurile distributiei normale se afla intre medie si o abatere standard deasupra mediei (z=+1)
Intre - 1z si +1z se afla aproximativ 68% dintre valorile distributiei
Aproximativ 96% dintre scoruri se afla intre -2z si +2z
Avand in vedere distributia scorurilor z pe o curba normala standardizata, aceasta poate fi utilizata pentru a afla raspuns la intrebari precum: Care este procentajul de valori care se afla sub/peste o anumita nota z; intre anumite note z; ori intre medie si o nota z? Care este nota z corespunzatoare unui anumit procentaj de valori? Pentru a raspunde la aceste intrebari, se utilizeaza o tabela speciala care contine, sub forma de probabilitati, frecventele valorilor de sub curba normala z (Anexa 1).
Asa cum vom vedea mai departe, curba normala are o importanta aparte pentru analiza statistica. Aceasta, deoarece se accepta faptul ca variabilele statistice s-ar distribui mai ales sub aceasta forma daca ar fi efectuate un numar mare (tinzand spre infinit) de masurari.
Exemple:
Sa ne raportam la distributia valorilor QI, pentru care media este egala cu 100 si abaterea standard 16
Exemplul 1 Care este procentajul oamenilor al caror scor QI este intre 100 si 110?
Pentru a raspunde la aceasta intrebare, convertim valorile QI in scoruri z. 100(QI)=0(z). Pentru 110(QI) se aplica formula:
Z=![]() =
=![]() =+0.63
=+0.63
Aria de sub curba normala cuprinsa intre valorile QI si 100 si 110 este reprezentata pe figura urmatoare:


Citim tabela ariilor la intersectia celulelor 0.6 cu 0.03. Valoarea este 0.2357 ceea ce, exprimat in procente, este 23.57%
Conchidem ca 23.57% din oameni au un QI cuprins intre 100 si 110)
Exemplul 2 Care este procentul oamenilor al caror QI este mai mare decat 125?
Convertim in note z:
z=![]() =
=![]() =+1.56
=+1.56
Aria de sub curba normala pentru scoruri QI mai mari decat 125 este reprezentata mai jos:
Citim valoarea din tabel care corespunde intersectiei celulei 1.5 cu 0.06, pentru a afla procentajul dintre medie si nota z +1.56. Gasim valoarea, exprimata in procente, 44.06%. Acesta este procentajul dintre medie si z=+1.56.
Stim ca procentajul peste medie este 50%, ca urmare, procentajul celor peste QI=125 va fi
50-44,06=5,94
Conchidem ca 5.94% dintre oameni au un QI mai mare de 125 (z=1,56)
Exemplul 3 Care este scorul minim pe care trebuie sa l obtina o persoana pentru a fi intre primii 5% din populatie?
Ne reprezentam aria de sub curba care delimiteaza cele mai mari 5% dintre valorile z, trebuind sa aflam valoarea corespunzatoare z, respectiv QI:
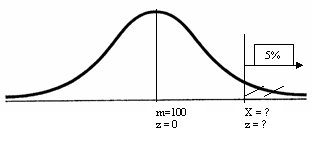

Aria dintre medie si linia noastra este 50%-5%=45%. Cautam in tabel valoarea ce mai apropiata de 0.45 si o gasim la intersectia celulelor 1.6 cu 0.04. Deci, z=1.64 pentru limita procentului de 5%.
Convertim scorul z=1.64 in valoare bruta; X=m+z*s=100+ (+1.64)*16=126.24
Conchidem ca pentru a fi in primii 5% trebuie sa obtinem un QI=126.24
Exemplul 4 Care este scorul care indica cei mai slabi 33%?
Ne reprezentam limita de 33% in zona valorilor de sub medie:


Cautam nota z corespunzatoare acestui procent.
![]()
Mai intai, scadem 33% din 50% cat reprezinta aria din partea
inferioara a curbei. Obtinem 17% Cautam nota z corespunzatoare procentului de 17% de sub
medie.
Valoarea 0.1700 (17%) se gaseste la intersectia celulelor 0.4 cu 0.04, ceea ce indica nota z=-0.44 (cu minus, pentru ca ne aflam in partea stanga a curbei).
Convertim nota z in valoare bruta: X=m+z*s=100+(-0.44)*16=92.96.
Conchidem ca este necesar un scor de cel mult 92.96 pentru a avea un QI intre ultimii 33%.
Valorile reprezentate pe curba normala nu reprezinta valori reale, rezultate in urma unui proces de masurare. Ele reprezinta valori ipotetice, distribuite astfel pe baza unui model matematic (legea numerelor mari). Nimic nu ne impiedica sa consideram ca valorile de sub curba normala sunt rezultatul unei ipotetice extrageri aleatoare. Pe masura ce "extragem" mai multe valori, curba de distributie a acestora ia o forma care se apropie de forma curbei normale. Extragand "la infinit" valori aleatoare, vom obtine o distributie normala perfecta, exprimabila printr-o curba normala perfecta.
Din cele spuse mai sus, rezulta faptul ca valorile din zona centrala a curbei sunt mai "frecvente" (mai multe), pentru ca aparitia lor la o extragere aleatoare este mai "probabila". In acelasi timp, valorile "mai putin probabile", apar mai rar, si populeaza zone din ce in ce mai extreme ale distributiei (curbei).
Probabilitatea inseamna "frecventa relativa a aparitiei unui eveniment". Subiectiv, se traduce prin "cat de siguri putem fi ca acel eveniment apare".
Daca probabilitatea reprezinta raportul dintre evenimentul favorabil si toate evenimentele posibile, atunci valoarea ei variaza intre 0 si 1. Ea poate fi exprimata si in procente. De exemplu, probabilitatea de 0.05 corespunde unui procentaj de aparitie de 5%
Utilizand simbolul p (de la "probabilitate"), spunem ca daca p<0.05 inseamna ca evenimentul are mai putin de 5% sanse sa apara, in conditiile unei distributii corespunzatoare curbei normale. Procentajul ariilor de sub curba normala poate fi citit, deci, si ca probabilitatea a distributiei. De exemplu, probabilitatea de a avea un scor intre medie si z=+1 este de 0.34. Probabilitatea de avea o nota z=+1.65 sau mai mare este p<0.05
Caracteristicile curbei normale si frecventa cu care se face apel la aceasta in studiile statistice determina adesea interpretari gresite. De aceea se cuvine sa insistam asupra faptului ca distributia normala reprezinta un model teoretic care aproximeaza de o maniera multumitoare cele mai multe dintre caracteristicilor fenomenelor naturale, incluzandu-le si pe cele psihice. Cu toate acestea, distributiile reale pe care le descopera psihologii in studiile lor nu au niciodata parametrii unei curbe normale perfecte. Acest lucru este practic imposibil daca ne gandim ca o curba normala are limitele deschise, mergand spre infinit, in timp ce distributiile reale sunt finite. In ciuda acestui neajuns, aproximarea oferita de modelul teoretic al curbei normale este considerata acceptabila din punct de vedere stiintific.
Un al aspect care poate conduce la interpretari eronate este exprimarea valorilor curbei normale in scoruri z. Acest fapt este interpretat uneori in sensul ca transformarea in scoruri z a unei oricarei distributii o transforma intr-o distributie normala. Este, evident, o concluzie gresita. Convertirea valorilor unei distributii in scoruri z nu modifica forma distributiei. Distributia normala z este o distributie teoretica in timp ce o distributie z oarecare are forma distributiei valorilor originale.
TEMA PENTRU ACASA
Sa presupunem ca evaluarea preferintei pentru risc la un grup de studenti aviatori a condus la o distributie de valori avand m=60 si s=8.
Presupunand ca preferinta pentru risc se distribuie in populatie dupa o curba normala, calculati raspunsul la urmatoarele intrebari:
a. Care este procentajul valorilor intre valoarea 70 si medie?
b. Care este procentajul valorilor mai mari decat 75?
c. Care este procentajul scorurilor dintre valoarea 55 si medie?
d. Care este procentajul scorurilor mai mici de 55?
e. care este procentajul scorurilor intre 62 si 70?
f. Care este probabilitatea de avea un scor mai mare de 80?
g. care este probabilitatea de a avea un scor mai mic de 50?
h. care este probabilitatea de a avea un scor cuprins intre 45 si 75?
i. Care este scorul minim pe care il poate avea o persoana pentru a intra in primii 10% dintre subiecti?
j. Care este scorul maxim pe care trebuie sa il obtina cineva pentru a se afla printre ultimii 15%?