
|
|
|
INTEGRALE DEFINITE ȘI NEDEFINITE
Nr. Crt
Domeniul maxim de definitie
Integrala Nedefinita
1
|R
![]()
2
(0,∞), a![]() R
R
![]()
3
(0,∞) sau (-∞,0)
![]()
4
|R
![]()
5
|R*
![]()
6
|R, n![]() R
R
![]()
7
(0,∞)
![]()
8
(0,∞)
![]()
9
(-∞,-a) sau (-a,a) sau (0,∞)
![]()
10
|R, a![]() (0,∞), a
(0,∞), a![]() 1
1
![]() C
C
11
|R
![]() C
C
12
(-∞,-a) sau (-a,a) sau (0,∞)
![]() C
C
13
|R, a![]() 0
0
![]() C
C
14
(-a,a),
a![]() 0
0
![]() C
C
15
|R
![]() C
C
16
(-∞,-a) sau (0,∞) a > 0
![]() C
C
17
|R
![]() C
C
18
|R
![]() C
C
19
![]() , k
, k![]() Z
Z
![]() C
C
20
![]() , k
, k![]() Z
Z
![]() C
C
21
![]() , k
, k![]() Z
Z
![]() C
C
22
![]() , k
, k![]() Z
Z
![]() C
C
Tabel integrale Tabel derivate
![]()
![]() c' = 0
c' = 0![]()
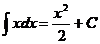 x' = 1
x' = 1
![]() (xn)' = nxn-1
(xn)' = nxn-1
![]() (
(![]() )' =
)' = ![]()
![]() dx =
dx = ![]() (ax)' = axlna
(ax)' = axlna
![]() (lnx)' =
(lnx)' = ![]()
![]() dx = e
dx = e![]() (ex)' = ex
(ex)' = ex
![]() (sinx)' = cosx
(sinx)' = cosx
![]() (cosx)' = -sinx
(cosx)' = -sinx
![]() (tgx)' =
(tgx)' = ![]()
![]() (ctgx)' =-
(ctgx)' =- ![]()
![]()
![]() ( arcsinx)' =
( arcsinx)' = ![]()
![]() + C (arccosx)' = -
+ C (arccosx)' = -![]()
![]() dx =
dx = ![]() (arctgx)' =
(arctgx)' = ![]()
![]() (arcctgx)' = -
(arcctgx)' = - ![]()
![]() + C(f.g)' = f'g +fg'
+ C(f.g)' = f'g +fg'
![]() (
(![]() )' =
)' = ![]()
![]() (cf)' = cf'
(cf)' = cf'
![]()
![]()
![]()
![]()
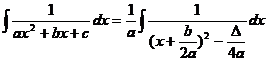
![]() Formula Leibnitz -
Newton ( integrale definite )
Formula Leibnitz -
Newton ( integrale definite )
INTEGRALE DEFINITE
SUME RIEMANN
Definiție: Se da colecția de obiecte:
[a,b] - interval inchis
- diviziune a intervalului [a,b]
= (a=x0<x1<x2<.<xn=b)
f:[a,b]R
I - un sistem de puncte intermediare cuprins in intervalul [a,b]
I [xi-1,xi]
Numim suma Riemann atașata funcției f, diviziunii și sistemului de puncte intermediare I numarul notat:
n
(f,i) = f(i)*(xi-xi-1)
i=1
INTEGRALE IN SENS RIEMANN
Definiție: Se da f:[a,b]R. Spunem ca funcția f este integrabila in sens Riemann daca if R a.i. >0, >0 cu proprietatea ca o diviziune a intervalului [a,b] si (i) un sistem de puncte intermediare, i [xi-1,xi] cu ||||< sa avem |(f,i) - if |<.
if - se numește integrala definita a funcției f pe intervalul [a,b]
b
notez: if = f(x)*dx.
a
b
Obs:
1) Numarul real if este unic; f(x)*dx este unica.
a
Demonstrație:
P.p.a. ca i1i2 care verifica condițiile din definiție, atunci pentru >0 k,>0 (k=1,2) astfel incat pentru orice diviziune:
=(x0,x1,.,xn) a lui [a,b] cu |||| < și orice puncte intermediare xi-1 i xi (1 i n) sa avem:
|(f,)-ik|</2 (k=1,2).
Luand = min(1, , 2,) rezulta ca pentru orice diviziune a lui [a,b] cu ||||< si orice sistem (i) de puncte intermediare asociat lui , avem:
|(f,)-i1| < /2 si |(f,)-i2| < /2,
deci: |i1- i2| < |i1- (f,)| + |(f,)-i2| < /2+/2 = .
Cum > 0 a fost luat arbitrar, rezulta i1=i2; dar din ipoteza i1i2 contradicție.
Deci if este unic.
2) f:[a,b]R
f - integrabila in sens Riemann pe [a,b] f marginita pe [a,b]
Demonstrație:
f - integrabila pe [a,b] if R a.i. o diviziune a lui [a,b] si >0, >0 pentru care ||||< |(f,i) - if |< i un sistem de puncte intemediare.
Arat ca f este marginita pe [xk-1,xk]
x, ik
Fie i=
xi, i=k
n n
(f,i) = f(i)*(xi-xi-1) = f(xi)*(xi-xi-1) + f(x)*(xk-xk-1)
i=1 i=1
ik
|(f,i) - if | <
- < (f,i) - if < /+ if
- + if < (f,i) < + if
n
- + if < f(xi)*(xi-xi-1) + f(x)*(xk-xk-1) < + if
i=1
ik
1/(xk-xk-1)*[ - + if - f(xi)*(xi-xi-1)] < f(x) < 1/(xk-xk-1)*[ - + if - f(xi)*(xi-xi-1)]
[] []
M1 M2
M1< f(x) < M2
f - marginita pe [xk-1,xk] k f - marginita pe [a,b]
3) f,g:[a,b] R
A[a,b]
A finita, cu proprietea:
i) g integrabila pe [a,b]
ii) f(x)=g(x) x[a,b]A
atunci: a) f - integrabila pe [a,b]
b b
b) g(x)*dx = f(x)*dx
a a
Demonstrație:
Este suficient ca demonstrația sa fie facuta pentru cazul cand mulțimea finita A este formata dintr-un singur punct c, deoarece cazul general se poate obține din acesta prin inducție. Presupunem deci A=.
Funcția g fiind integrabila, este marginita, deci M1 0 astfel incat:
|g(x)| M1 x[a,b]
Luand M = max( M1, |f(c)| ) f(x) M si g(x) M x[a,b].
g - integrabila > 0, ' > 0 a.i.:
b
1) | (g,i) - g(x)*dx | < /2
a
= (x0, x1,.,xn), cu |||| < ' si sistemul de puncte intermediare i.
Luand = min (', /(8*M) ), avem si 4*M* /2.
Daca c este un punct al diviziunii , atunci 0 i n astfel incat c = xj. In acest caz singurele puncte intermediare care ar putea coincide cu c sunt punctele j sau j+1. Deci ținand seama de faptul ca f(x) = g(x) x c, obținem:
| (g,i) - (f,i) | = | ( g(i) - f(i) )*( xi - xi-1 )| | g(j) - f(j)|*(xj - xj-1) + | g(j+1) - - f(j+1)|*(xj+1 - xj) 4*M*|||| < 4*M* < /2
(xk-1,xk). Deci singurul punct intermediar care ar putea coincide cu c este punctul k, prin urmare:
| (g,i) - (f,i) | = | ( g(i) - f(i) )*( xi - xi-1 )| | g(k) - f(k)|*(xk - xk-1) 2*M*|||| 2*M* < /2
Din analiza facuta pana acum rezulta ca:
2) | (g,i) - (f,i) | < /2
Din 1) si 2) obtinem:
b
| (f,i) - g(x)*dx | <
a
b b
adica f este integrabila si: f(x)*dx = g(x)*dx.
EXEMPLE:
1) f:[a,b] R
f(x) = k
a
f - integrabila si k*dx = k*(b-a)
b
if = k*(b-a) a.i. > 0 > 0 cu proprietatea ca = (x0=a<x1<.<xn=b) si
i [xi-1,xi], ||||< |(f,i) - if |<
(f,i) = f(i)*(xi-xi-1) = k(xi-xi-1) = k* (xi-xi-1) = k(x1-x0+x2-x1+.+xn-xn-1) =
= k*(xn - x0) = k*(b-a)
|(f,i) - if | = |k*(b-a) - k*(b-a)| = 0 < >0.
2) f,g:[a,b] R
1, pentru xQ -1, pentru xQ
f(x) = g(x) =
-1, pentru xRQ 1, pentru xRQ
f,g - nu sunt integrabile
Demonstratie pentru f(x) :
Fie = (a=x0<x1<.<xn=b), avem:
1*(xi - xi-1) = b-a, pentru i Q
(f,) =
(-1)*(xi - xi-1) = a-b, pentru i RQ
Cum limita sumelor integrale depinde de alegerea punctelor i, funcția nu este integrabila.
Demonstrația se face analog pentru g(x).
Desi f,g nu sunt integrabile funcțiile:
(f+g)(x) = 0 x[a,b]
(f*g)(x) = -1 x[a,b]
(fog)(x) = 1 x[a,b]
sunt integrabile ca fiind funcții constante.
3) Sa se cerceteze integrabilitatea funcției:
0, daca x este irațional sau x = 0
G(x) =
1/q, daca x = p/q, p/q fracție ireductibila
Rezolvare: Funcția este integrabila pe segmentul [0,1]. Intr-adevar fie N un numar ales arbi-trar. Sa consideram multimea tuturor punctelor rationale din intervalul [0,1] avand numitorul mai mic decat N. Exista un numar finit de astfel de puncte, fie acesta k. Fie o diviziune arbi-trara a segmentului [0,1]. Exista cel mult 2k intervale partiale (pe care le notam d1',d2',.,d2k') care sa contina cele k puncte considerate anterior. Fiind dat >0, vom alege di-viziunea in asa fel incat suma lungimilor celor 2k intervale sa fie inferioara numarului /2. Aceasta se poate realiza alegand norma diviziunii suficeint de mica. Notam d1", d2",. d2m" celelalte intervale partiale ale diviziunii. Intervalele di" (i = 1, 2, ., m) contin, in afara de puncte irationale in care valoarea functiei este 0, puncte rationale de forma x = p/q, q>N, si astfel ca G(p/q) = =1/q<1/N. Deci :
2k m
Sd(G) - sd(G) = (Mi' - mi')i' + (Mi" - mi")i"
i=1i=1
Am notat cu Mi', respectiv mi' marginea supearioara, respectiv marginea inferiaora a functiei in intervalul di' si cu Mi", respectiv mi" marginea supearioara, respectiv marginea inferiaora a functiei in intervalul di", i' este lungimea lui di', iar i" este lungimea lui di".
Deoarece Mi' - mi'<1, mi" = 0, Mi"<1/N, i, avem
2k m
Sd(G) - sd(G) < i' + (1/N)* i" < /2 + 1/N.
i=1 i=1
Daca N > 2/, atunci 1/N < /2 si Sd(G) - sd(G) < .
Putem calcula efectiv valoarea integralei. Deoarece in orice interval valoarea minima a
1
functiei este 0, avem sd(G) = 0, ; rezulta I = G(x)dx = 0. Datorita integrabilitatii functiei
0
G, avem :
1
G(x)dx = 0.
0
Integrabilitatea functiei se mai putea stabili tinand seama de faptul ca multimea puncte-lor ei de discontinuitate este multimea numerelor rationale care este numarabila, deci neglija-bila.
TABEL CU INTEGRALE NEDEFINITE
g:A A , g(x) = xn, nєN
xn dx =xn+1/(n+1) + ζ
g: IA , I Ì (0,¥ )
g(x) = xa, aєA -
xa dx =xa+1/(a+1) + ζ
g: IA , IÌ (0,¥ )
g(x) = 1/x = x -1
1/x dx =ln |x|+ζ = ln x+ζ, x>0
ln(-x)+ζ,x<0
g:A A , g(x) = ax, a > 0, a ¹ 1
ax dx =ax/lna + ζ
g: I A , I Ì (-¥ , -a) sau I = (-a,a) sau
I = (a,¥ ) ,g(x) = 1/(x2-a2)
dx/(x2-a2) = (1/2a)ln |(x-a)/(x+a)| + ζ
g:A A , g(x) = 1/(x2+a2), a ¹ 0
dx/(x2+a2)=(1/a) arctg(x/a) + ζ
g: I A , I Ì (-a,a), g(x) = 1/ , a¹ 0
dx/
g:A A , g(x) =1/, a ¹ 0
dx/ =ln(x+) + ζ
g: IA , I Ì (-¥ , -a) sau I = (a,¥ )
a > 0, g(x) = 1/
dx/ =ln|x+| + ζ
g:A A , g(x) = sinx
sinx dx = - cos x + ζ
g:A A , g(x) = cosx
cosx dx = sin x + ζ
g:IA , I Ì ((2k+1)p /2,(2k+3)p /2), kєZ, g(x) = 1/cos2x
dx/cos2x = tg x + ζ
g:I![]() A , I Ì (kp ,(k+1)p ), kєZ,
A , I Ì (kp ,(k+1)p ), kєZ,
g(x) = 1/sin2x
dx/sin2x = - ctg x + ζ
g:I![]() A , I Ì ((2k+1)p /2,(2k+3)p /2), kєZ, g(x) = tgx
A , I Ì ((2k+1)p /2,(2k+3)p /2), kєZ, g(x) = tgx
tgx dx = - ln|cos x| + ζ
g:I![]() A , IÌ (kp ,(k+1)p ), kєZ,
A , IÌ (kp ,(k+1)p ), kєZ,
g(x) = ctgx
ctgx dx = ln|sin x| + ζ
g:A A , g(x) = shx = (ex-e-x)/2
shx dx = ch x + ζ
g:A A , g(x) = chx = (ex+e-x)/2
chx dx = sh x + ζ