|
|
|
Proprietatile planelor simplu si dublu particulare
a) Proprietatile planelor simplu particulare
Datorita pozitiei lor in spatiu planele simplu particulare au urmatoarele proprietati, numite proprietati metrice. In cele ce urmeaza ele sunt prezentate pentru planul fronto-orizontal.
|
|
Fig. 9 Fig. 10
Orice punct cuprins in planul fronto-orizontal are proiectia laterala situata pe urma laterala (inclinata) a planului.
Aceasta
proprietate este o consecinta a pozitiei planului
fronto-orizontal (perpendicular pe planul lateral). Proiectanta oricarui
punct din plan fata de planul lateral este o dreapta a planului
fronto-orizontal si intersecteaza [W] intr-un punct ce apartine
atat planului lateral cat si planului fronto-orizontal, deci intr-un punct
apartinand urmei laterale a planului. In figurile 9 si 10 fiecare
dintre punctele A(35, 30, 5), B (10, 30, 5) si C(10, 5, 30) apartin
planului fronto-orizontal definit prin punctele PZ (0, 0, 40)
si PY(0, 40, 0) pentru ca proiectiile lor laterale apartin
urmei laterale.
Definitie
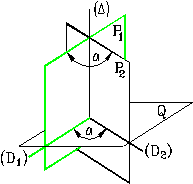
Unghiul dintre doua plane concurente este unghiul masurat intr-un plan perpendicular pe dreapta lor de intersectie si for-mat de dreptele de intersectie dintre plane si planul normal.
Fig. 11
In figura 11 unghiul a din spatiu dintre planele [P1] si [P2] se masoara in planul [Q] D [P1] ∩ [P2], intre dreptele (D1) si (D2), (D1) [P1] ∩ [Q] si (D2) [P2] ∩ [Q].
Pe baza acestei defintii se poate enunta urmatoarea proprietate a planului fronto-orizontal:
P7
Unghiurile pe care le formeaza in spatiu planul fronto-orizontal cu planul vertical si cu planul orizontal sunt unghiurile dintre urma laterala (PW) si axele (OZ) si respectiv (OY').
Se constata din figura 9 ca unghiul dintre planul fronto-orizontal [P] si planul vertical este unghiul masurat in planul [W] intre dreptele de intersectie (OZ) [P] ∩ [V] si (PW) [P] ∩ [W]. In epura se rega-seste acelasi unghi intre (OZ) si (PW).
b) Proprietatile planelor dublu particulare
Proprietatile planelor dublu particulare reprezinta particularizari ale proprietatilor planelor simplu particulare.
Astfel, pentru planul de profil [R] [H] si [R] [V] T [R] [W] proprietatile P6 si P7 devin:
Orice punct cuprins intr-un plan de profil are proiectiile verticala si orizontala situate pe urmele omonime (cu acelasi nume) ale planului.
P9
Unghiurile pe care le formeaza in spatiu planul de profil cu planul vertical si cu planul orizontal sunt unghiurile pe care le formeaza urma verticala (PV) si urma orizontala (PH) cu axa (OX).
Pentru ca planul de profil este paralel cu planul lateral, acestor doua proprietati li se adauga o a treia:
Orice figura cuprinsa intr-un plan de profil se proiecteaza in adevarata marime pe planul lateral.
|
|
Fig. 12 Fig. 13
In figurile 12 si 13 este exemplificat cazul unui plan de profil [R] care contine un cerc de centru C(30, 25, 23) de raza r = 14 mm. Toate punctele semnificative ale cercului - centrul C si punctele diametral opuse 1, 2, 3, 4 - apartin planului si cercul se proiecteaza in adevarata marime pe planul lateral dar deformat pe planul orizontal (ca segmentul (2-4) si pe planul vertical ca segmentul (1' -3').
