MARIMILE DISPERSIEI

Descrierea unei distributii de scoruri cu ajutorul marimilor tendintei centrale nu epuizeaza informatia relevanta statistic despre distributia respectiva. Pentru descrierea completa a unei distributii de scoruri trebuie sa consideram si marimile dispersiei. Aceste marimi furnizeaza informatie despre eterogenitatea sau varietatea unei distributii de scoruri.

De pilda, o medie aritmetica de 6,33 poate fi obtinuta dintr-o multime de scoruri similare, concentrate in jurul acestei valori - precum 6, 6, 7 - sau dintr-o multime de scoruri nesimilare, imprastiate in raport cu aceasta valoare - precum 1, 8, 10. In cazul unor scoruri similare sau cu variabilitate scazuta, media aritmetica este mai adecvata pentru masurarea tendintei centrale decat in cazul unor scoruri nesimilare sau cu variabilitate inalta. Luand un exemplu pur didactic, informatia conform careia media aritmetica a varstelor dintr-un esantion este de 25 de ani este relevanta daca varstele subiectilor din esantion sunt relativ grupate in jurul aceste valori si este neimportanta daca esantionul respectiv este alcatuit din doua grupuri, unul cu varste cuprinse intre 1 si 10 ani, celalalt cu varste cuprinse intre 40 si 50 de ani.

In aceasta sectiune sunt introduse cele mai des folosite marimi ale dispersiei: indicele variatiei calitative, amplitudinea si amplitudinea intercuartilica, abaterea medie, varianta, abaterea standard si coeficientul de variatie. Fiecare dintre aceste marimi furnizeaza o indicatie precisa a eterogenitatii unei distributii de scoruri.

1 INDICELE VARIATIEI CALITATIVE

Indicele variatiei calitative (IQV)[1] reprezinta raportul dintre variatia observata efectiv intr-o distributie de scoruri si variatia maxim posibila pentru acea distributie. IQV poate lua valori cuprinse intre 0,00 (nici o variatie sau variatie nula) si 1,00 (variatie maxima). Acest indice se foloseste in mod obisnuit pentru variabile masurate la nivel nominal, putand fi utilizat si pentru variabile masurate la celelalte nivele, daca scorurile respective sunt grupate in distributii de frecvente.

Pentru ilustrare, sa presupunem ca un cercetator este interesat in compararea eterogenitatii religioase a trei colectivitati - A, B si C -, datele obtinute fiind cele din tabelul urmator:

Tabelul 3.9 Apartenenta religioasa in trei colectivitati

Simpla inspectie a datelor din acest tabel arata ca, dintre cele trei colectivitati, A este cea mai putin eterogena. Mai exact, eterogenitatea religioasa in colectivitatea A este nula, intrucat toti membrii acestei colectivitati sunt crestin-ortodocsi. Apoi, colectivitatea C este cea mai eterogena, B situandu-se intre A si C. Sa vedem acum cum sunt reflectate aceste observatii de catre IQV, a carui formula de calcul este urmatoarea:

Formula 3.7 IQV =

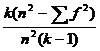
in care k = numarul de categorii

n = numarul total de cazuri din cele k categorii

= suma patratelor frecventelor din fiecare categorie

Sa aplicam aceasta formula la fiecare dintre cele trei distributii de frecvente. Pentru aceasta, trebuie sa calculam mai intai suma patratelor frecventelor respective. Astfel, pentru colectivitatea A, avem:

= 90² + 0² + 0² = 8100

IQV =

Intrucat valorile pentru k si n sunt aceleasi in toate cele trei distributii, IQV pentru celelalte doua colectivitati poate fi calculat schimband doar valorile pentru . Pentru colectivitatea B, avem:

= 60² + 20² + 10² = 4100

IQV =

Pentru colectivitatea C:

= 30² + 30² + 30² = 2700

IQV =

Dupa cum se poate constata, IQV reflecta cantitativ si precis observatiile de mai sus. Colectivitatea A prezinta o variatie nula a variabilei masurate (IQV = 0), colectivitatea C prezinta variatia maxim posibila pentru aceste date (IQV = 1,00), iar colectivitatea B se situeaza intre A si C, cu o variatie substantiala (IQV = 0,74).

2 AMPLITUDINEA SI AMPLITUDINEA INTERCUARTILICA

Amplitudinea (A) este o marime a dispersiei usor de calculat, cu care ne-am intalnit deja in capitolul anterior, definita drept diferenta dintre cel mai mare scor si cel mai mic scor din multimea scorurilor date:

A = X_max - X_min

Pentru datele din tabelul 2.4, de pilda, A = 69 - 24 = 45. In cazul unei distributii de frecvente cu date grupate, amplitudinea absoluta se aproximeaza prin diferenta dintre limita de clasa reala superioara a ultimului interval si limita de clasa reala inferioara a primului interval[2]:

A = LCRS_max - LCRI_min

Astfel, pentru datele din tabelul 3.6, A 69,5 - 19,5 = 50.

Amplitudinea intercuartilica (Q) se defineste ca diferenta dintre cea de-a treia si prima cuartila a unei distributii de scoruri ordonate crescator:

Q = Q₃ - Q₁

Sa consideram din nou un exemplu prezentat in sectiunea 3.2. Fie urmatoarea multime ordonata de 15 scoruri:

2, 4, 4, 5, 7, 8, 10, 12, 17, 18, 18, 21, 27, 29, 30

Q₁ Q₃

In acest exemplu, A = 30 - 2 = 28 si Q = 21 - 5 = 16.

Intrucat ia in considerare doar scorurile extreme dintr-o distributie, A nu este o marime suficient de semnificativa a dispersiei. Pot fi intalnite distributii in care scorurile extreme sunt foarte departate de scorurile intermediare, caz in care aprecierea dispersiei pe baza amplitudinii este o greseala. De asemenea, amplitudinea nu ofera informatii despre natura scorurilor dintre cele doua extreme: daca scorurile sunt grupate in centrul distributiei, daca sunt imprastiate omogen intre cele doua scoruri extreme, daca sunt concentrate in doua grupe, cate una langa fiecare extrema, distributia fiind bimodala etc. Q ia in considerare 50% dintre cazurile aflate in centrul distributiei[3] si astfel evita problema de a fi o marime bazata pe scorurile extreme. Pe de alta parte, intrucat, ca si A, ia in considerare doar doua scoruri dintr-o distributie, Q nu ofera informatie despre natura scorurilor dintre cele doua scoruri considerate, astfel ca impartaseste celelalte dezavantaje asociate cu A. Totusi, aceste marimi sunt utile atunci cand dorim sa obtinem rapid o masura a variabilitatii unei distributii si, mai ales, atunci cand dorim sa realizam rapid o comparatie intre variabilitatile a doua distributii cu un numar egal de scoruri. Sa presupunem, de pilda, ca am inregistrat varstele subiectilor din doua esantioane, obtinand urmatoarele date:

Esantionul 1     11, 16, 18, 23, 29, 31, 37

Esantionul 2     18, 19, 21, 23, 24, 26, 29

Mediile aritmetice pentru cele doua esantioane sunt si , mediana fiind aceeasi pentru ambele esantioane: 23. Intrucat amplitudinea varstelor din primul esantion, 26, este mai mare decat amplitudinea varstelor din cel de-al doilea esantion, 11, primul esantion este mai eterogen din punctul de vedere al varstelor.[4]

3 ABATEREA MEDIE SI VARIANTA

Marimile dispersiei expuse in continuare capteaza ideea de variabilitate a unei distributii de scoruri de interval sau de raport fata de centrul acelei distributii, mai precis, fata de media sa aritmetica si folosesc toate scorurile distributiei.

Stim ca intr-o distributie de scoruri de interval sau de raport cu media aritmetica , diferenta X_i - reprezinta abaterea scorului X_i fata de media aritmetica . O sugestie pentru a obtine o marime mai adecvata a dispersiei ar fi sa insumam toate abaterile scorurilor individuale fata de medie si sa impartim suma astfel obtinuta la numarul total de scoruri, n. Mai stim, insa, ca pentru orice distributie de scoruri, suma abaterilor scorurilor de la media lor aritmetica este egala cu zero, -) = 0, astfel ca rezultatul impartirii acestei sume la n ar fi intotdeauna 0. Pentru a folosi cumva sugestia mentionata, avem la dispozitie doua posibilitati: sau neglijam semnele abaterilor, considerand valorile absolute ale acestora[5], sau ridicam la patrat abaterile, intrucat daca se inmultesc doua numere care au semnul minus, produsul este pozitiv.

Prima posibilitate conduce la o marime a dispersiei, numita abaterea medie si notata cu , a carei formula de calcul este urmatoarea:

Formula 3.8

Cea de-a doua posibilitate conduce la o alta marime a dispersiei, numita varianta[6], notata cu s² atunci cand este vorba despre un esantion si cu σ² atunci cand este vorba despre o populatie. Formula de calcul a variantei pentru populatii este urmatoarea:

Formula 3.9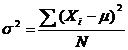    

in care μ = media aritmetica a populatiei

N = numarul total de scoruri din populatie

Formula de calcul a variantei pentru esantioane difera de formula 3.9 sub doua aspecte: in locul mediei aritmetice a populatiei (μ) apare media aritmetica a esantionului (), iar la numitor, in locul numarului total de scoruri din populatie (N) apare numarul total de scoruri din esantion diminuat cu o unitate (n - 1)[7].

Formula 3.10

Pentru a ilustra calculul abaterii medii si al variantei, vom folosi datele din tabelul 3.2, adaugand o coloana pentru modulele diferentelor si, pentru o simplificare pe care o vom folosi ulterior, o coloana pentru patratele scorurilor individuale, X_i²:

Tabelul 3.10 Calculul abaterii medii si al variantei ()

Pentru datele din acest exemplu, avem:

De notat ca varianta calculata cu ajutorul formulei 3.9 reprezinta patratul mediu al abaterilor, i.e. media aritmetica a patratelor abaterilor scorurilor populatiei de la media lor aritmetica μ.

In cazul esantioanelor mari, aplicarea formulei definitionale 3.10 poate fi greoaie, mai ales daca valoarea pentru contine zecimale, ceea ce presupune multe rotunjiri. Din formula 3.10 se pot deduce alte formule de calcul care, aplicate la aceleasi date, produc aceleasi rezultate ca si formula 3.10 si care permit calcularea mai usoara si mai rapida a variantei[8]. Prezentam in continuare doua astfel de formule, in care nu mai este nevoie de calcularea diferentelor X_i - .

Formula 3.11

Formula 3.12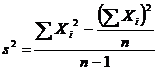

Aplicand formula 3.11 la datele din exemplul de mai sus, avem:

Desi pare mai complicata decat formula 3.10, formula 3.12 ne scuteste de calcularea mediei aritmetice a scorurilor, astfel incat pentru calcularea variantei cu ajutorul acestei formule este nevoie doar de scorurile individuale. In exemplul nostru:

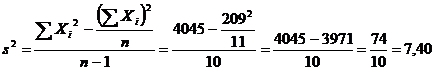
Formulele de calcul simplificat al variantei pentru populatii difera de formulele de mai sus prin aceea ca se inlocuieste cu μ, iar n - 1 devine N.

4 ABATEREA STANDARD SI COEFICIENTUL DE VARIATIE

Calculul variantei implica ridicarea la patrat a abaterilor scorurilor individuale fata de media lor aritmetica (formulele 3.9 si 3.10). In consecinta, unitatea atasata variantei este patratul unitatii atasate scorurilor individuale respective. Daca, de pilda, este vorba despre scoruri exprimate in ani, varianta va fi exprimata in ani la patrat. Pentru a se obtine o marime a variabilitatii care sa fie exprimata in aceleasi unitati in care sunt exprimate scorurile respective, se ia radacina patrata a variantei, s sau σ. Aceasta marime statistica se numeste abatere standard si, in cazul esantioanelor, se defineste cu ajutorul urmatoarei formule:

Formula 3.13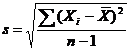

Relatia dintre abaterea standard si varianta fiind , valoarea abaterii standard pentru datele din tabelul 3.10 este = 2,72.

Corespunzator formulelor 3.11 si 3.12, avem urmatoarele formule de calcul simplificat al abaterii standard:

Formula 3.14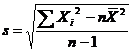

Formula 3.15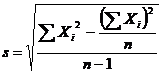

Coeficientul de variatie al unei distributii de scoruri (CV) se defineste ca raportul dintre abaterea standard a distributiei si media sa aritmetica. De obicei, coeficientul de variatie se inmulteste cu 100 si se prezinta ca procent. Astfel, avem:

Formula 3.16

In exemplul folosit pana acum, CV = (2,72/19) · 100 = 143,16. Evident, in cazul populatiilor, s se inlocuieste cu σ, iar cu μ. Coeficientul de variatie este cu deosebire util atunci cand se doreste compararea variabilitatii a doua distributii de scoruri cu medii aritmetice sensibil diferite.

5 CALCULUL ABATERII STANDARD PENTRU DATE GRUPATE

Formula de calcul a abaterii standard pentru date grupate se obtine pe baza formulei 3.15. Pentru a aplica formula 3.15 trebuie sa cunoastem trei valori: suma scorurilor, ΣX_i, suma patratelor scorurilor, ΣX_i², si numarul de scoruri, n. Atunci cand datele au fost grupate in distributii de frecvente nu cunoastem distributia exacta a scorurilor individuale si deci nu putem determina exact primele doua valori. Intr-un astfel de caz, suma scorurilor se aproximeaza, ca si pentru media aritmetica, inmultind numarul de cazuri din fiecare interval, f_i, cu centrul intervalului respectiv, m_i, si insumand aceste produse: Σf_im_i. Suma patratelor scorurilor se aproximeaza ridicand la patrat centrele de interval, inmultind fiecare patrat astfel obtinut cu numarul de cazuri din intervalul respectiv si insumand aceste produse: Σf_im_i². Avem astfel:

ΣX_i Σf_im_i

ΣX_i² Σf_im_i²

Formula care da valoarea aproximativa a abaterii standard pentru date grupate se obtine facand substitutiile corespunzatoare in formula 3.15. Obtinem astfel:

Formula 3.17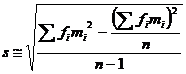

Pentru ilustrare, vom folosi datele din tabelul 3.7, in care vom adauga doua coloane: una pentru patratele centrelor de interval si una pentru produsele dintre patratele centrelor de interval si frecvente:

Tabelul 3.11 Calculul abaterii standard

pentru date grupate

Totalul ultimei coloane este valoarea pentru Σf_im_i². Aplicand formula 3.17 la aceste date obtinem:

===

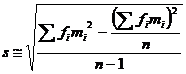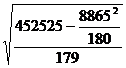=== 9,43

De notat ca, pentru datele negrupate corespunzatoare acestui exemplu, abaterea standard calculata cu ajutorul uneia dintre formulele 3.13 - 3.15 este egala cu 9,00.

Pentru a descrie adecvat o distributie de scoruri trebuie sa raspundem la trei intrebari: Care este forma distributiei? Care este scorul sau mediu? Cat de variate sunt scorurile? Modalitatile de raspuns la prima intrebare au fost discutate in capitolul 2. Raspunsurile la ce-a de-a doua intrebare au fost abordate in prima parte a acestui capitol. Am vazut ca in statistica, "scor mediu" are trei intelesuri diferite, carora le corespund trei marimi statistice: media aritmetica, mediana si modul. Media aritmetica, aplicabila numai pentru date de interval sau de raport, exprima scorul tipic al unei distributii. Mediana poate fi folosita si pentru nivelul ordinal de masura si reflecta scorul central al unei distributii. Modul poate fi folosit la orice nivel de masura si reprezinta cel mai intalnit scor intr-o distributie. In plus, am prezentat modalitati de descriere a pozitiei scorurilor individuale intr-o distributie de interval sau de raport: percentilele si rangul percentilelor. In capitolul urmator vom prezenta un alt cadru de referinta pentru interpretarea scorurilor individuale: scorurile standard.

In cea de-a doua parte a acestui capitol am prezentat modalitati de a raspunde la cea de-a treia intrebare: indicele variatiei calitative, amplitudinea si amplitudinea intercuartilica, abaterea medie, varianta, abaterea standard si coeficientul de variatie. Abaterea standard este cea mai des folosita marime a dispersiei pentru date de interval si de raport, avand avantajul de a fi exprimata in aceleasi unitati de masura ca si scorurile respective. Valoarea abaterii standard este cu atat mai mare, cu cat distributia scorurilor este mai eterogena sau, altfel spus, cu cat variabilitatea distributiei este mai mare. Reciproc, valoarea abaterii standard este cu atat mai mica, cu cat distributia scorurilor este mai omogena sau, altfel spus, cu cat variabilitatea distributiei este mai mica. Daca fiecare caz intr-o distributie ar avea acelasi scor, atunci abaterea standard pentru distributia respectiva ar fi 0. Astfel, abaterea standard nu are limita superioara, iar limita sa inferioara este 0. Abaterea standard isi dovedeste utilitatea mai ales atunci cand se doreste compararea a doua sau mai multe distributii. De asemenea, dupa cum vom vedea in capitolul urmator, abaterea standard este implicata si in calculul scorurilor standard si in notiunea de distributie normala standard.

GLOSAR

Abatere standard: radacina patrata a catului dintre suma abaterilor patratice ale scorurilor fata de media lor aritmetica si n 1 pentru esantioane sau N pentru populatii.

Abatere medie: media aritmetica a sumei abaterilor absolute ale scorurilor fata de media lor aritmetica.

Amplitudinea absoluta: diferenta dintre cel mai mare scor si cel mai mic scor dintr-o multime de scoruri.

Amplitudine intercuartilica: diferenta dintre cea de-a treia si prima cuartila a unei distributii de scoruri ordonate crescator.

Asimetrie: proprietatea unei multimi de scoruri de a avea putine scoruri foarte mari (asimetrie pozitiva) sau putine scoruri foarte mici (asimetrie negativa).

Coeficient de variatie: raportul dintre abaterea standard  a unei distributii de scoruri si media sa aritmetica. De obicei, coeficientul de variatie se inmulteste cu 100 si se prezinta ca procent.

Indicele variatiei calitative: raportul dintre variatia observata efectiv intr-o distributie de scoruri si variatia maxim posibila pentru acea distributie.

Interval modal: intervalul de clasa care contine cel mai mare numar de cazuri.

Marimile tendintei centrale: marimi statistice care rezuma o intreaga distributie de scoruri, descriind cea mai tipica sau centrala valoare a distributiei respective sub forma unui singur numar sau a unei singure categorii.

Marimile dispersiei: marimi statistice care furnizeaza informatie despre eterogenitatea sau varietatea unei distributii de scoruri.

Medie aritmetica ponderata: media aritmetica a mai multor grupuri combinate.

Medie aritmetica: rezultatul impartirii sumei tuturor scorurilor dintr-o multime de scoruri la numarul total de scoruri din acea multime.

Mediana: punct intr-o multime de scoruri fata de care numarul de cazuri cu scoruri mai mici sau egale este egal cu numarul de cazuri cu scoruri mai mari sau egale .

Mod: scorul care apare cel mai frecvent intr-o multime de scoruri.

Percentila: valoarea P_m a unei multimi de scoruri fata de care cel mult m% din scoruri sunt mai mici decat m si cel mult (100 - m)% din scoruri sunt mai mari decat m.

Varianta: catul dintre suma abaterilor patratice ale scorurilor fata de media lor aritmetica si n 1 pentru esantioane sau N pentru populatii.