
|
|
|
DISTRIBUTIA NORMALA
Notiunea de distributie normala este de mare importanta in statistica. Pe de o parte, distributia normala poate fi folosita in combinatie cu abaterea standard pentru a formula enunturi descriptive precise despre distributiile scorurilor unor variabile. Pe de alta parte, distributia normala sta la baza multor tehnici statistice inferentiale.
1 CARACTERISTICILE DISTRIBUTIEI NORMALE
Distributia normala este o distributie teoretica de scoruri unimodala, simetrica si continua. Graficul unei distributiei normale are forma de clopot cu ambele extremitati extinse la infinit[1]. Ca atare, un astfel de grafic, numit si curba normala[2], nu atinge axa orizontala sau, altfel spus, este asimptotic fata de axa orizontala, dupa cum se ilustreaza in figura 1.
Figura 1 Un exemplu de curba normala
![]()
![]()
![]()

![]()
Distributia normala este un model teoretic ce poate fi folosit pentru a descrie distributii particulare ale scorurilor unor variabile masurate la nivel de interval sau de raport, despre care s-a constatat ca aproximeaza suficient normalitatea intr-o populatie, precum coeficientul de inteligenta, rezultatele obtinute la diferite teste de cunostinte sau numarul de erori comise in indeplinirea anumitor sarcini. Scorurile unor astfel de variabile tind sa se grupeze simetric in jurul scorului central, dand nastere unui grafic de distributie in forma de clopot. Daca distributia scorurilor unei variabile intr-o populatie aproximeaza normalitatea, se spune ca variabila respectiva este normal distribuita in populatia respectiva sau, pe scurt, ca variabila respectiva este normala. Pe de alta parte, dupa cum vom vedea in capitolele urmatoare, distributia normala poate fi folosita pentru a reprezenta diferite marimi statistice care rezulta din studierea unor esantioane dintr-o populatie data, ceea ce permite obtinerea unor concluzii despre valorile pentru populatie pe baza valorilor cunoscute pentru esantioane. Utilizarea distributiei normale in statistica face apel la asa-numitele scoruri standard sau scoruri Z.
2 CALCULUL SCORURILOR STANDARD
Scorurile standard, numite si scoruri Z, folosesc abaterea standard ca unitate de masura si descriu pozitia relativa a unui scor individual in raport cu intreaga multime de scoruri din care face parte. Formula de calcul pentru scorurile Z ale unei populatii este urmatoarea:
Formula 1 ![]()
Aceasta formula transforma orice scor "brut" X in scorul Z corespunzator. Numaratorul fractiei, X - μ, indica distanta in unitati brute a scorului X fata de media aritmetica. Prin impartirea acestei distante la σ aflam distanta in abateri standard sau fractiuni de abateri standard a scorului X fata de medie. Corespunzator, formula de calcul pentru scorurile Z ale unui esantion este urmatoarea:
Formula 2 ![]()
Pentru
ilustrare, sa consideram o distributie de scoruri pentru un
esantion, in care ![]() = 100 si s = 20. In acest caz, scorurile Z
corespunzatoare scorurilor brute 85, 120 si 150 sunt:
= 100 si s = 20. In acest caz, scorurile Z
corespunzatoare scorurilor brute 85, 120 si 150 sunt:
![]()
![]()
![]()
Fiecare dintre aceste scoruri Z arata la cate abateri standard fata de media aritmetica se afla scorul brut corespunzator. Un scor Z negativ arata ca scorul brut se afla sub media aritmetica, iar un scor Z pozitiv arata ca scorul brut este mai mare decat media aritmetica. Evident, un scor Z egal cu 0 arata ca scorul brut corespunzator este egal cu media aritmetica.
Se demonstreaza ca daca toate scorurile unei distributii particulare se transforma in scoruri Z, atunci:
q Forma distributiei scorurilor Z este aceeasi cu cea a distributiei initiale;
q Media aritmetica a distributiei scorurilor Z este 0, indiferent de valoarea mediei aritmetice a distributiei initiale;
q Abaterea standard a distributiei scorurilor Z este 1, indiferent de valoarea abaterii standard a distributiei initiale.
Aceste proprietati au fost generalizate in studiul distributiei normale standard.
3 DISTRIBUTIA NORMALA STANDARD
Ca si in cazul unei distributii particulare de scoruri de interval sau de raport, distributia normala poate fi descrisa cu ajutorul mediei sale aritmetice si a abaterii standard. Intrucat oricarei perechi de valori pentru media aritmetica si abaterea standard ii corespunde o distributie normala, matematic vorbind exista o infinitate de distributii normale, ale caror forme exacte depind de marimile mentionate. Pentru a descrie efectiv distributiile unor variabile normale, in analiza statistica se considera o distributie normala particulara, numita distributia normala standard. Variabila corespunzatoare distributiei normale standard este numita variabila normala standard, valorile acestei variabile fiind scoruri Z. Din acest motiv, aceasta distributie se mai numeste si distributia Z. Prin conventie, media aritmetica a distributiei normale standard se ia ca origine a variatiei variabilei normale standard, ceea ce inseamna ca aceasta distributie are media aritmetica egala cu 0. De asemenea, se considera ca abaterea standard a distributiei normale standard este egala cu unitatea.
Graficul corespunzator distributiei normale standard este numit curba normala standard. Aria delimitata de curba normala standard este proportionala cu frecventa scorurilor, astfel ca proportia de cazuri cuprinse intre un scor Z si media aritmetica poate fi aflata cu ajutorul calculului integral. Statisticienii au determinat cu precizie aceste arii, rezultatele fiind organizate sub forma unui tabel, numit tabelul curbei normale standard sau tabelul ariilor de sub curba normala standard (vezi Anexa A). Schema generala a acestui tabel este prezentata in figura 2.
Figura 2 Schema tabelului curbei normale standard
Z
0,00
0,01
0,02
0,03
0,04
0,05
0,0
0000
![]()
0,1
0,2
0,3
0,4
![]()
1736
0,5
In corpul tabelului apar numere alcatuite din patru cifre. Aceste numere reprezinta ariile cuprinse intre un scor Z dat si media aritmetica. Numerele inscrise in prima coloana din stanga, etichetata Z, reprezinta primele doua cifre ale unui scor Z, iar numerele inscrise pe primul rand de sus reprezinta cea de-a treia cifra. De pilda, pentru a afla aria cuprinsa intre un scor Z = 0,45 si media aritmetica, se coboara in prima coloana din stanga pana la 0,4 (primele doua cifre ale scorului Z considerat) si apoi se parcurge spre dreapta randul respectiv pana cand se ajunge sub 0,05 (cea de-a treia cifra). Numarul gasit la intersectia acestor doua coordonate este 1736, care poate fi citit sau ca un procent (17,36%), sau ca o proportie (0,1736). In primul caz vom spune ca 17,35% din aria totala a curbei normale standard se afla intre scorul Z = 0,45 si media aritmetica (punct in care Z = 0); in cel de-al doilea caz vom spune ca proportia din aria totala a curbei normale standard cuprinsa intre scorul Z = 0,45 si media aritmetica este de 0,1736. Intrucat orice curba normala este simetrica, aceeasi procedura se aplica si pentru afla aria cuprinsa intre un scor Z negativ si media aritmetica. Astfel, rezultatul de mai sus poate fi interpretat spunand ca 17,35% din aria totala a curbei normale standard se afla intre scorul Z = 0,45 si media aritmetica.
4 UTILIZAREA DISTRIBUTIEI NORMALE STANDARD
Figura 3 ilustreaza utilizarea tabelului distributiei normale standard pentru determinarea procentelor din aria delimitata de curba normala, aflate intre un scor Z dat si media aritmetica (Z = 0).
Figura 3 Procente din aria de sub curba normala
![]()
0 +2 +3 +1 0,13% 0,13% 2,15% 13,59% 13,59% 2,15% -3 -1 -2 95,44% 68,26%
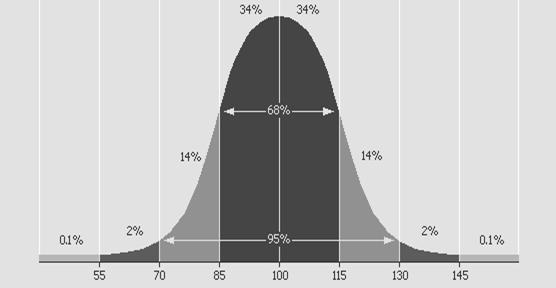
Abateri standard fata de media aritmetica
De pilda, din tabel aflam ca intre Z = +1 si media aritmetica se afla 34,13% din aria de sub curba (v. intersectia coordonatelor 1,0 si 0,00). Intrucat curba este simetrica, procentul din arie cuprins intre Z = 1 si media aritmetica este tot de 34,13%. Astfel, intre 1 abateri standard fata de medie se afla 68,26% din aria totala. Similar, intre Z = +2 si medie se afla 47,72% din arie, astfel ca intre 2 abateri standard fata de medie se afla 94,44% din arie.
Intrucat un procent relativ mic din aria totala se afla peste +3 abateri standard sau sub 3 abateri standard (0,13%), pentru scopuri practice, ilustrate in cele ce urmeaza, se considera ca distributia normala se extinde de la Z 3,59 la Z +3,59 sau, altfel spus, la 3,59 abateri standard de o parte si de cealalta a mediei aritmetice, scorurile Z aflate dincolo de aceste limite fiind considerate a fi egale cu 0.
In cazul variabilelor normal distribuite pentru care cunoastem media aritmetica si abaterea standard, distributia normala standard poate fi folosita pentru a determina diferite procente sau proportii de cazuri in distributii particulare, precum si pentru a determina probabilitatea de a selecta la intamplare un scor cuprins intr-o plaja data de scoruri ale unei distributii aproximativ normale.
1 DETERMINAREA PROCENTELOR DE CAZURI
Sa
consideram o distributie de scoruri a variabilei coeficient de
inteligenta (IQ) pentru un esantion de1000 de subiecti
cu ![]() = 100 si s = 20, ilustrata in figura
= 100 si s = 20, ilustrata in figura
Figura 4 Distributia scorurilor IQ pentru
un esantion de 1000 de subiecti
![]()
0,13% 0,13% 2,15% 13,59% 13,59% 2,15% 160 40 140 80 60 120 95,44% 68,26%

Unitati IQ
Sa presupunem ca ne intereseaza procentul de cazuri cu scoruri IQ mai mici decat 115. Calculam mai intai scorul Z corespunzator scorului brut 115:
![]()
Din tabelul curbei normale aflam ca aria dintre scorul Z = +0,75 si media aritmetica reprezinta 27,34% din aria totala. Intrucat aria aflata sub media aritmetica reprezinta 50% din aria totala, procentul de subiecti cu scoruri IQ mai mici decat 115 este de 74,34% (27,34% + 50%). Acest rezultat poate fi exprimat si in numar de cazuri, spunand ca aproximativ 743 de subiecti din esantionul considerat (74,34% din 1000) au scoruri IQ mai mici decat 115.
Sa presupunem acum ca ne intereseaza procentul de cazuri cu scoruri IQ mai mici decat 75. Scorul Z corespunzator scorului brut 75 este
![]()
Pentru a afla aria de sub un scor Z negativ, aria dintre scor si media aritmetica se scade din 50% (aria aflata la stanga mediei). Din tabelul curbei normale aflam ca aria dintre scorul Z = 1,25 si media aritmetica reprezinta 39,44% din aria totala. Astfel, procentul de subiecti cu scoruri CI mai mici decat 75 este de 10,56% (50% 39,44%), ceea ce inseamna ca aproximativ 394 de subiecti (39,44% din 1000) au scoruri IQ mai mici decat 75.
Acelasi model de calcul se utilizeaza pentru a afla aria situata deasupra unui scor Z pozitiv. Sa presupunem ca ne intereseaza procentul de cazuri cu scoruri mai mari decat 150. Stim ca scorul Z corespunzator acestui scor brut este +2,50. Din tabelul curbei normale aflam ca aria dintre scorul Z = +2,50 si media aritmetica reprezinta 47,98% din aria totala, astfel ca procentul de subiecti cu scoruri mai mari decat 150 este de 2,02% (50% 47,98%). Aceasta inseamna ca aproximativ 20 de subiecti (2,02% din 1000) au scoruri IQ mai mari decat 150.
In general, ariile situate peste sau sub un anumit scor Z se determina conform urmatoarelor reguli:
1. Pentru a determina aria aflata sub un scor Z negativ sau peste un scor Z pozitiv, aria dintre scorul respectiv si media aritmetica se scade din 50%.
2. Pentru a determina aria aflata sub un scor Z pozitiv sau peste un scor Z negativ, aria dintre scorul respectiv si media aritmetica se aduna cu 50%.
Sa vedem acum felul in care se determina ariile, respectiv procentele de cazuri dintre doua scoruri. Sa presupunem ca ne intereseaza procentul de subiecti cu scoruri IQ cuprinse intre 95 si 125. Scorurile Z corespunzatoare acestor scoruri brute sunt
![]()
![]()
Din tabelul curbei normale aflam ca aria dintre scorul Z = 0,25 si media aritmetica reprezinta 9,87% din aria totala si ca aria dintre scorul Z = +1,25 si media aritmetica reprezinta 39,44% din aria totala. Fiind vorba despre scoruri aflate de o parte si de alta a mediei, aria dintre scoruri se determina adunand ariile dintre fiecare scor si media aritmetica. Astfel, procentul de subiecti cu scoruri IQ cuprinse intre 95 si 125 este de 49,31% (9,87% + 39,44%). Aceasta inseamna ca aproximativ 439 de subiecti au scoruri IQ cuprinse intre 95 si 125.
Pentru a determina aria dintre doua scoruri aflate de aceeasi parte a mediei aritmetice, se determina mai intai ariile dintre fiecare scor si medie, dupa care aria mai mica se scade din aria mai mare. Sa presupunem ca ne intereseaza procentul de subiecti cu scoruri IQ cuprinse intre 115 si 125. Stim ca scorul Z corespunzatoare scorurilor brute 115 si 125 sunt, respectiv, +0,75 si +1,25. Stim, de asemenea, ca intre Z = +0,75 si media aritmetica se afla 27,34% din aria totala si ca intre Z = +1,25 si media aritmetica se afla 39,44% din aria totala. Prin urmare, procentul de subiecti cu scoruri IQ cuprinse intre 115 si 125 este de 12,10% (39,44% 27,34%), ceea ce inseamna ca aproximativ 121 de subiecti au scoruri IQ cuprinse intre 115 si 125. Acelasi model de calcul se utilizeaza atunci cand ambele scoruri se afla sub medie.
2 DETERMINAREA PROBABILITATILOR PENTRU SCORURI
Tabelul curbei normale standard poate fi utilizat pentru a determina probabilitatea de a selecta la intamplare un scor cuprins intr-o plaja data de scoruri ale unei distributii aproximativ normale. Inainte de a considera acest tip de utilizare, sa examinam pe scurt notiunea de probabilitate.
Pentru a estima probabilitatea producerii unui eveniment, trebuie sa definim evenimentele care reprezinta cazuri favorabile. Un caz favorabil este un caz in care se produce evenimentul a carui probabilitate de aparitie dorim sa o estimam sau, pe scurt, un caz care realizeaza acel eveniment. Sa presupunem ca intr-o urna sunt n bile de culori diferite, dintre care exact m sunt albe si ca ne intereseaza probabilitatea de a extrage de la prima incercare o bila alba. Evenimentul fiind aparitia unei bile albe, cazul favorabil este extragerea unei bile albe. Fata de cazul favorabil, vom spune ca extragerea unei bile de orice culoare este un caz egal posibil. Avem astfel m cazuri favorabile si n cazuri egal posibile. Probabilitatea teoretica a unui eveniment E, notata Pr(E) se defineste ca raportul dintre numarul m al cazurilor favorabile si numarul n al cazurilor egal posibile:
![]()
Pentru ilustrare, sa presupunem ca in urna se afla 52 de bile de culori diferite, dintre care una singura este alba. Intrucat m = 1 si n = 52, probabilitatea de a extrage de la prima incercare o bila alba este 1/52. Aceasta fractie poate fi exprimata si ca proportie, impartind numaratorul la numitor: (1/52) = 0,0192. Vom spune ca aparitia bilei albe la o singura extragere se produce in proportie de 0,0192. In stiintele omului, probabilitatile sunt exprimate in mod obisnuit ca proportii si vom urma aceasta conventie in continuare.
Este important de remarcat ca, gandite astfel, probabilitatile au un inteles precis: pe termen lung, cazurile favorabile se afla intr-o anumita relatie proportionala cu numarul total de cazuri. In exemplul nostru, probabilitatea de 0,0192 ca bila alba sa apara la o singura extragere inseamna de fapt ca din 10000 de extrageri a cate unei bile din urna completa, proportia de extrageri a bilei albe va fi de 0,0192 sau, altfel spus, ca din 10000 de extrageri a cate unei bile din urna completa, bila alba va aparea de 192 de ori, celelalte 9808 extrageri producand bile de alte culori.
Acum, din cele de mai sus stim ca pentru orice distributie particulara aproximativ normala, proportiile prezentate in tabelul curbei normale standard ne dau frecventa relativa a cazurilor cu scoruri cuprinse intre un anumit scor si media aritmetica, precum si ca probabilitatea unui eveniment este frecventa relativa a cazurilor care realizeaza acel eveniment. Prin urmare, proportiile din tabelul curbei normale standard pot fi interpretate ca probabilitati si pot fi folosite pentru a determina probabilitatea de selectie a unui scor cuprins intr-o plaja data de scoruri ale unei distributii aproximativ normale.
Considerand din nou distributia variabilei coeficient de inteligenta cu care am lucrat mai sus, sa presupunem ca ne intereseaza probabilitatea ca un subiect ales la intamplare sa aiba un scor IQ cuprins intre 95 si scorul mediu de 100 (aici, cazul favorabil este selectarea unui subiect al carui scor se afla in amplitudinea de scoruri specificata[3]). Scorul Z corespunzator scorului brut de 95 este 0,25 si, conform tabelului curbei normale standard, proportia din arie cuprinsa intre scorul Z = 0,25 si media aritmetica este de 0,0987. Aceasta proportie este probabilitatea cautata. Vom spune ca probabilitatea ca un subiect ales la intamplare sa aiba un scor IQ cuprins intre 95 si 100 este de 0,0987 sau, rotunjit, de 0,1 sau de unu la zece.
De notat ca pentru determinarea probabilitatilor de selectare a scorurilor se utilizeaza aceleasi proceduri ilustrate mai sus pentru determinarea procentelor de cazuri, diferenta fiind aceea ca proportiile din tabelul curbei normale standard sunt interpretate ca probabilitati. De pilda, probabilitatea ca un subiect ales la intamplare din esantionul considerat sa aiba un scor IQ peste 95 este de 0,5987 (0,5000 + 0,0987).
Sa mai notam ca, intrucat in distributia normala standard cele mai multe scoruri sunt grupate in jurul mediei aritmetice, frecventa acestora scazand pe masura ce ne indepartam de medie, daca vom selecta la intamplare un numar de scoruri dintr-o distributie aproximativ normala, vom selecta mai des scoruri apropiate de media aritmetica si mai rar scoruri aflate mult sub sau peste medie.
[1] Distributia normala a fost studiata pentru prima data in secolul al XVIII-lea de catre Abraham De Moivre. La inceputul secolului al XIX-lea a fost descoperita independent de Carl Friedrich Gauss si Pierre Simon de Laplace.
[2] In onoarea matematicienilor Gauss si Laplace, curba normala este cunoscuta si sub numele de clopotul lui Gauss sau curba Gauss-Laplace.
[3] Determinarea probabilitatii cautate cu ajutorul formulei de calcul pentru probabilitati ar conduce la construirea unei fractii care sa aiba drept numarator numarul de subiecti ale caror scoruri se afla in amplitudinea specificata si drept numitor numarul total de subiecti.