
|
|
|
UNIVERSITATEA "DUNAREA DE JOS" GALATI
Facultatea de Inginerie Electrica si Electronica
PROBABILITATI SI STATISTICA IN INGINERIE
-Probleme Propuse Seminar-
1.Consideratii Teoretice
1.1. NOTIUNI GENERALE
Variabila aleatoare este o marime care poate capata, in urma unui experiment, o valoare oarecare necunoscuta uneori. Variabila aleatoare se noteaza cu litera mare A, B, , X, Y, iar valorile sale posibile se noteaza cu litere mici a1, a2, , an; , y1, y2, , yn. Variabila aleatoare prezinta doua componente: o caracteristica exprimata cantitativ sau calitativ si o posibilitate de realizare exprimata prin probabilitate. Variabilele aleatoare pot fi discrete sau continue.
1.2.Variabilele aleatoare discrete
Daca in urma unei experiente variabila X ia valorile izolate x1, x2, , xn, aceasta este discreta (ex. Numarul pieselor defecte intr-un esantion). Numarul valorilor posibile "n" ale variabilei aleatoare X poate fi finit sau infinit. Probabilitatea aparitiei fiecarei valori este:
P(x=x1) = p1; P(x=x2) = p2; P(x=xn) = pn (1)
Enumerarea tuturor valorilor posibile ale unei variabile aleatoare si a probabilitatilor respective se numeste repartitie. Repartitia variabilei discrete se prezinta sub forma unui tablou de repartitie:
X :
sau X :
(2)
Legea de repartitie stabileste relatia analitica ce leaga valoarea xi de probabilitatea respectiva si se numeste functie de probabilitate:
P(x=xi) = P(xi) = pi (3)
Reprezentarea grafica a repartitiei se poate face sub forma unei diagrame cu bare (fig. 1.a) sau sub forma unei diagrame poligonale (fig. 1.b).
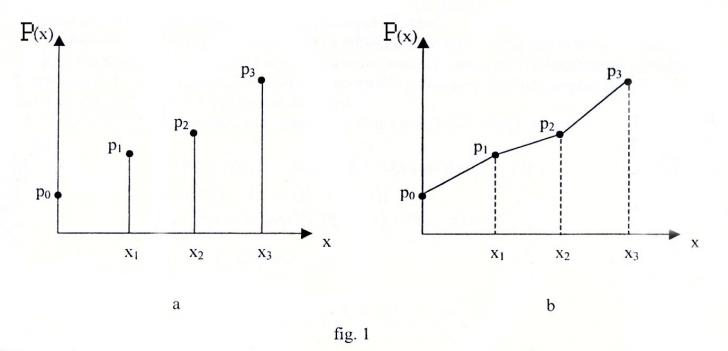
Totalitatea valorilor distincte si posibile x1, x2, , xn formeaza un sistem complet de evenimente incompatibile. Probabilitatile de aparitie ale acestora indeplinesc:
= 1
(4)
Probabilitatea
evenimentului ( X ≤ x ),
x
(x1, .., xn) reprezinta
functia de repartitie a variabilei aleatoare X:
F(x) = P( X ≤ x ) (5)
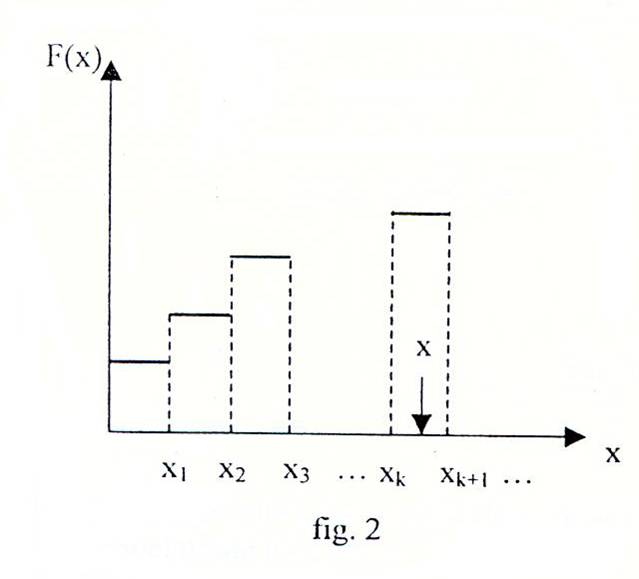
Functia de repartitie este caracteristica cea mai reprezentativa a unei variabile aleatoare, iar pentru variabila discreta, aceasta se reprezinta sub forma unei diagrame discontinue in trepte (fig. 2).
Daca se cunoaste functia de probabilitate a unei variabile aleatoare discrete P(xi), functia de repartitie se poate exprima conform relatiei urmatoare:
F(x) = P(X<x) = P(X≤xk) = P((X=x1)
(X=x2)
(X=xk))
=
(6)
1.3.Variabile aleatoare continue
O variabila aleatoare, care poate lua valori intr-un interval (o infinitate de valori), nu poate fi redata prin tabloul de repartiție specific variabilei discrete.
Functia ce cuantifica probabilitatea ca variabila aleatoare X sa ia valori in intervalul
(x<X≤x +Δx), cu Δx foarte mic (sa ia valoarea aproximativ x), este functia densitate de repartitie a probabilitatii f(x) sau, pe scurt, densitatea de probabilitate (analog, functiei de probabilitate corespunzatoare variabilelor aleatoare discrete).
Probabilitatea ca o variabila aleatoare X sa ia valori in intervalul Δx este:
P(x<X≤(x+ Δx)) = P((X≤(x+ Δx))∩(X>x)) = P((X≤(x+Δx))∩(X≤x)) = P(X≤( x+Δx)) - P(X≤x) = =F(x+Δx)-F(x) (7)
Functia densitate de probabilitate este:
f(x) =
=
= F′(x)
(8)
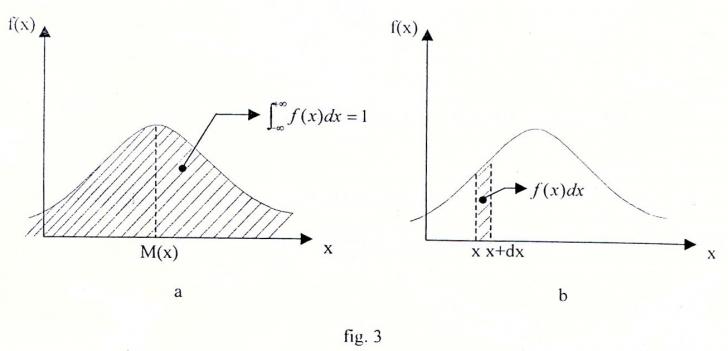
Functia densitate de probabilitate f(x) este prima derivata a functiei repartitie F(x).
Curba densitatii de probabilitate, reprezentata in fig. 3.a are valoarea maxima in punctul x=M(X), iar marimea f(x)dx (aria hasurata in fig. 3.b) reprezinta probabilitatea ca variabila aleatoare sa se gaseasca in intervalul elementar dx, fiind egala din punct de vedere geometric cu aria dreptunghiului elementar cu baza dx din fig. 3.b.
Functia de repartitie pentru variabila aleatoare continua X se exprima, cu ajutorul functiei densitate de probabilitate f(x), astfel:
F(x)=
(9)
si este reprezentata de aria hasurata cuprinsa intre curba densitate de probabilitate si axa absciselor (fig. 4), iar aria totala delimitata de curba f(x) are valoarea 1 (fig. 3.a).
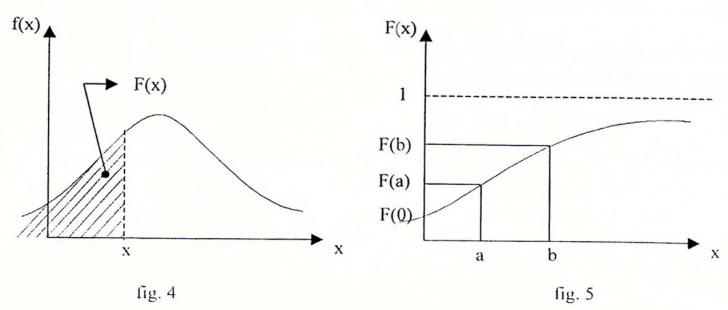
In fig. 5 se prezinta functia de repartitie F(x) a variabilei aleatoare X, ce ia valori in intervalul [0,1], tinzand asimptotic catre valoarea 1.
Proprietatile functiei de repartitie sunt:
a) F(-∞) = 0
b)
F(+∞) =
= 1 (10)
c) F(x1) ≤ F(x2) pentru x1≤x2 (functie nedescrescatoare)
Apartenenta unei variabile aleatoare la un interval dat
Exista
aplicatii in care este necesara determinarea probabilitatii
ca o variabila aleatoare X sa aiba valori cuprinse in intervalul
[a,b), X
[a,b).
Se considera evenimentele:
X < b,X < a,a ≤ X < b (11)
in care exista relatiile:
(X <
a)
(a ≤ X
< b) = (X < b)
(X < a) ∩ (a ≤ X < b) =
(12)
Conform relatiilor (12) avem:
P(X
< b) = P(X < a) + P(a ≤ X
< b)
P(a ≤ X < b) = P(X < b) - P(X < a) = F(b) - F(a)
P(a
≤ X < b) =
(13)
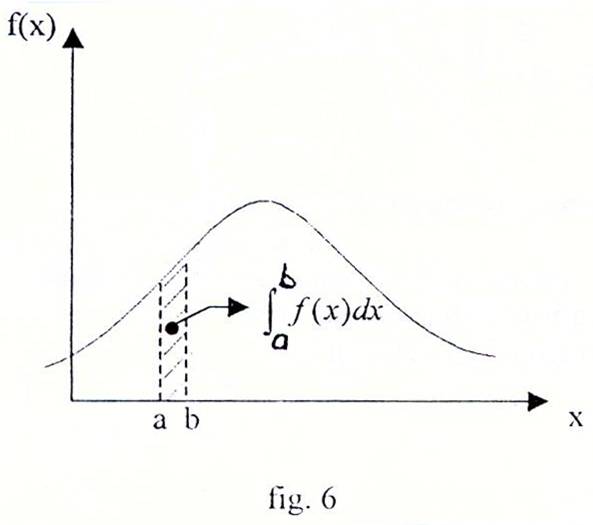
Conform relatiei (13), probabilitatea ca o variabila aleatoare sa apartina intervalului [a, b) este egala cu suprafata hasurata din fig. 6, suprafata limitata de curba f(x), axa absciselor si dreptele x=a, x=b.
2. Probleme Propuse:
2.1. Problema 1:
Se considera:
Experimentul de aruncare al zarului cu 6 fete.
Variabila aleatoare discreta X cu valori exprimate
de numarul
, care apare in urma experimentului.
Se cere:
Evaluarea sub forma de tablou, diagrama cu bare si diagrama poligonala a repartitiei variabilei aleatoare X.
Evaluarea si reprezentarea functiei de repartitie a variabilei aleatoare X.
Sa se verifice proprietatile functiei densitate de probabilitate si functiei de repartitie a variabilei aleatoare X.
Rezolvare:
Pentru M=1.9 se vor lua 100 de valori din tabelul 1 anexa dupa formula 10*M pana la 10*M+99 , adica de la n=19 pana la n=118
Aceste rezultate se trec in tabelul 2, iar in tabelul 3 se grupeaza rezultatele in functie de valoarea i rezultata in urma experimentului.
Cu datele din tabelul 1 se pot construi:
tabloul variabilei aleatoare X;
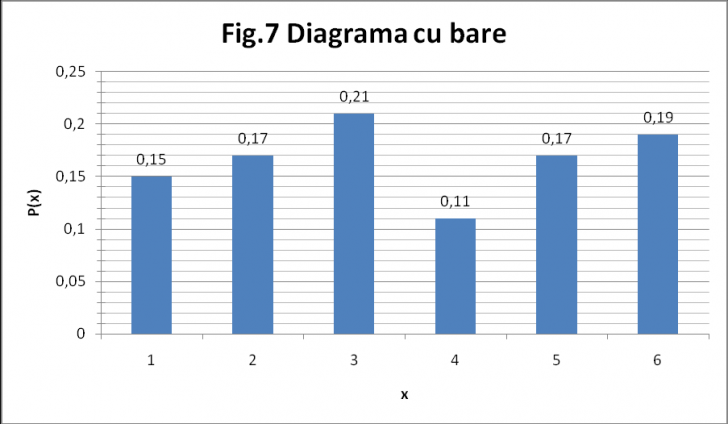
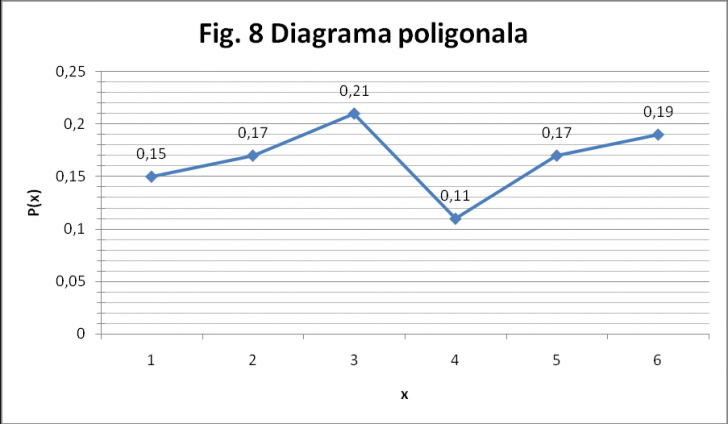
diagrama cu bare (fig7) si diagrama poligonala a repartitiei variabilei aleatoare discrete X (fig8);
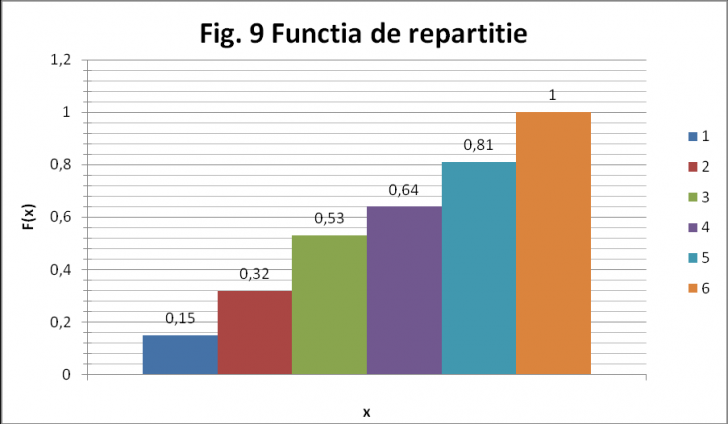
Se evalueaza functia de repartitie a variabilei aleatoare X si se exprima grafic (fig9).
Se verifica faptul ca multimea de evenimente formeaza un sistem complet de evenimente.
N = numarul de incercari.
f(i) = frecventa de aparitie a fetei i.
a(i) = f(i)/N = frecventa relativa de aparitie a fetei i.
Tabelul 1 (Rezultatul a 100 de incercari de aruncare a zarului):
1.
5
21.
3
41.
2
61.
5
81.
3
2.
5
22.
5
42.
6
62.
1
82.
3
3.
6
23.
1
43.
5
63.
5
83.
4
4.
2
24.
5
44.
5
64.
6
84.
6
5.
2
25.
3
45.
1
65.
6
85.
5
6.
6
26.
1
46.
6
66.
4
86.
1
7.
3
27.
3
47.
1
67.
3
87.
6
8.
6
28.
3
48.
2
68.
5
88.
2
9.
6
29.
3
49.
5
69.
6
89.
6
10.
3
30.
1
50.
4
70.
3
90.
5
11.
2
31.
1
51.
3
71.
3
91.
5
12.
5
32.
6
52.
6
72.
4
92.
6
13.
4
33.
2
53.
1
73.
3
93.
5
14.
2
34.
1
54.
2
74.
3
94.
5
15.
2
35.
3
55.
1
75.
3
95.
1
16.
2
36.
6
56.
4
76.
3
96.
6
17.
2
37.
2
57.
1
77.
4
97.
1
18.
4
38.
2
58.
1
78.
3
98.
2
19.
4
39.
6
59.
3
79.
2
99.
5
20.
3
40.
2
60.
4
80.
6
100.
4
Tabelul 2 (Evaluare sub forma de tablou):
I
F(i)
A(i)
1
15
0.15
2
17
0.17
3
21
0.21
4
11
0.11
5
17
0.17
6
19
0.19
|
N = 100
|
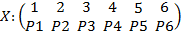
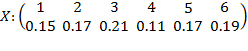
a(1)=F(1)/N=15/100=0.15;
a(2)=F(2)/N=17/100=0.17;
a(3)=F(3)/N=21/100=0.21
a(4)=F(4)/n=11/100=0.11;
a(5)=F(5)/N=17/100=0.17;
a(6)=F(6)/N=19/100=0.19
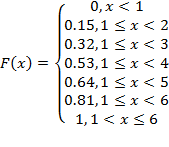
multimea de evenimente
formeaza un sistem complet de evenimente.
Fig. 7 (Diagrama cu bare a repartitiei variabilei aleatoare discrete X)
Fig. 8 (Diagrama poligonala a repartitiei variabilei aleatoare discrete X)
Fig. 9 (Functia de repartitie a variabilei aleatoare X)
2.2. Problema 2
Se considera:
Experimentul de masurare a tensiunii retelei de alimentare cu energie electrica (220/380, 50 Hz).
Variabila aleatoare continua X, cu valori exprimate de marimea xε(210, 230) V C.A. care se determina in urma experimentului.
Se cere:
Reprezentarea functiei densitate de probabilitate a variabilei aleatoare X.
Reprezentarea functiei de repartitie a variabilei aleatoare X.
Sa se verifice proprietatile functiei densitate de probabilitate si functiei de repartitie a variabilei aleatoare X.
Sa se evalueze probabilitatea ca variabila aleatoare X sa apartina intervalului [a, b).
Rezolvare
Se citesc valorile indicate de multimetrul numeric la intervale de timp egale, efectuandu-se 100 de citiri.
Se ordoneaza valorile tensiunii masurate, in ordine crescatoare si se realizeaza tabelul 3.
Se impart aceste valori in sapte intervale de grupare.
Se trec valorile astfel grupate in tabelul 4 si se calculeaza valoarea centrala a fiecarui grup, evaluandu-se:
- frecventa absoluta fj (numar de valori in clasa j);
- frecventa relativa aj (numar de valori in clasa j, raportat la numarul total de valori);
- frecventa cumulata:
- in valori
- in valori
Pentru reprezentarea functiei densitate de probabilitate a variabilei aleatoare X studiate se reprezinta punctele xj, aj si se unesc printr-o curba continua.
Se reprezinta grafic si functia de repartitie a variabilei aleatoare X unind punctele xj, Σaj printr-o curba continua.
Se verifica: functia densitate de probabilitate este prima derivata functiei de repartitie. In acest scop se iau doua valori suficient de apropiate xj1, xj2 si se verifica egalitatea:
[F(xj2)-F(xj1)]/(xj2-xj1)≈f(xj) unde xj este media valorilor xj1, xj2.
Se verifica faptul ca aria delimitata de functia f(x) are valoarea aproximativ 1.
Se verifica faptul ca functia de repartitie F(x) este nedescrescatoare si ia valori in intervalul [0, 1) tinzand catre 1.
Se evalueaza probabilitatea ca variabila aleatoare X sa apartina intervalului [215, 225), prin planimetrarea ariei delimitata de curba f(x) si de dreptele x=215, x=225.
Tabelul 3
n
x
n
x
n
x
n
x
n
x
1
210
21
215
41
218
61
221
81
223
2
210
22
215
42
218
62
221
82
224
3
210
23
215
43
218
63
221
83
224
4
211
24
215
44
219
64
221
84
224
5
211
25
216
45
219
65
221
85
224
6
212
26
216
46
219
66
221
86
224
7
212
27
216
47
219
67
221
87
225
8
212
28
216
48
219
68
222
88
225
9
212
29
216
49
219
69
222
89
225
10
213
30
216
50
219
70
222
90
225
11
213
31
217
51
219
71
222
91
225
12
213
32
217
52
220
72
222
92
226
13
213
33
217
53
220
73
222
93
226
14
214
34
217
54
220
74
222
94
226
15
214
35
217
55
220
75
223
95
226
16
214
36
217
56
220
76
223
96
227
17
214
37
218
57
220
77
223
97
227
18
214
38
218
58
220
78
223
98
227
19
215
39
218
59
220
79
223
99
228
20
215
40
218
60
221
80
223
100
229
Tabelul 4
Nr. clasei j
Interval de grupare
(xj1,xj2)
Valoare centrala xj
Frecventa simpla
Frecventa cumulata
absoluta fj
relativa
aj=fj/n
i
i
1
(210,212)
211
9
0.09
0.09
9
2
(213,215)
214
15
0.15
0.24
24
3
(216,218)
217
19
0.19
0.43
43
4
(219,221)
220
24
0.24
0.67
67
5
(222,224)
223
19
0.19
0.86
86
6
(225,227)
226
12
0.12
0.98
98
7
(228,230)
229
2
0.02
1
100
fj = frecventa absoluta (numarul de valori in clasa j).
aj = frecventa relativa (numarul de valori din clasa j, raportat la numarul total de valori).
N = 100
Fig. 10 (Functia densitate de probabilitate)
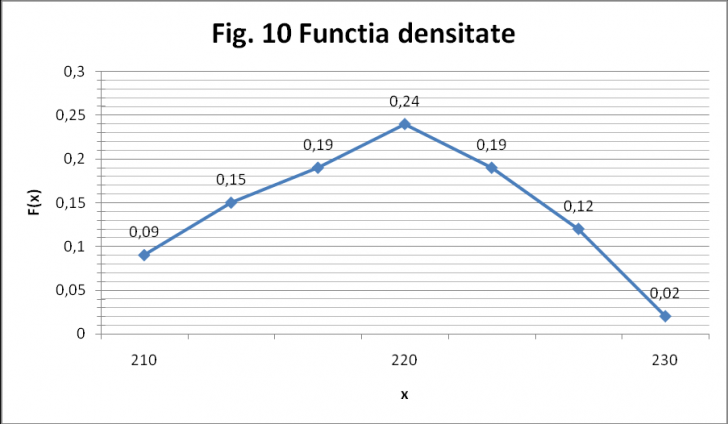
Fig. 11 (Functia de repartitie)
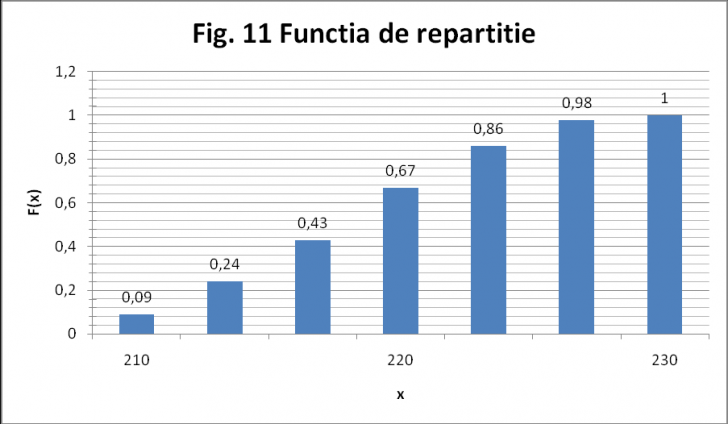
Proprietațile functiei de repartitie:
F(210) = P(210) = 0.03
F(212) = P(210) + P(211) + P(212) = 0.03 + 0.02 + 0.04 = 0.09
F(212) - F(210) / (212 - 210) = (0.09 - 0.03) / (212 - 210) = 0.06 / 2 = 0.03 = f(211)
F(213) = P(210) + P(211) + P(212) + P(213)= 0.03 + 0.02 + 0.04 + 0.04 = 0.13
F(215) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 = 0.24
F(215) - F(213) / (215 - 213) = (0.24 - 0.13) / (215 - 213) = 0.11/2 = 0.055 = f(214)
F(216) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 = 0.3
F(218) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) = = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 = 0.43
F(218) - F(216) / (218 - 216) = (0.43 - 0.3) / (218 - 216) = 0.13/2 = 0.065 = f(217)
F(219) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 = 0.51
F(221) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) + P(220) + P(221) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 + 0.08 + 0.08 = 0.67
F(221) - F(219) / (221 - 219) = (0.67 - 0.51) / (221 - 219) = 0.16 / 2 = 0.08 = f(220)
F(222) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) + P(220) + P(221) +P(222) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 + 0.08 + 0.08 + 0.07 = 0.74
F(224) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) + P(220) + P(221) +P(222) + P(223) + P(224) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 + 0.08 + 0.08 + 0.07 + 0.07 + 0.05 = 0.86
F(224) - F(222) / (224 - 222) = (0.86 - 0.74) / (224 - 222) = 0.12/ 2 = 0.06 = f(223)
F(225) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) + P(220) + P(221) +P(222) + P(223) + P(224) + P(225)= 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 + 0.08 + 0.08 + 0.07 + 0.07 + 0.05 + 0.05 = 0.91
F(227) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) + P(220) + P(221) +P(222) + P(223) + P(224) + P(225) + P(226) + P(227) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 + 0.08 + 0.08 + 0.07 + 0.07 + 0.05 + 0.05 + 0.04 + 0.03 = 0.98
F(227) - F(225) / (227 - 225) = (0.98 - 0.91) / (227 - 225) = 0.07/ 2 = 0.035 = f(226)
F(228) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) + P(220) + P(221) +P(222) + P(223) + P(224) + P(225) + P(226) + P(227) +P(228) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 + 0.08 + 0.08 + 0.07 + 0.07 + 0.05 + 0.05 + 0.04 + 0.03 + 0.01 = 0.99
F(230) = P(210) + P(211) + P(212) + P(213) + P(214) + P(215) + P(216) + P(217) + P(218) + P(219) + P(220) + P(221) +P(222) + P(223) + P(224) + P(225) + P(226) + P(227) +P(228) + P(229) + P(230) = 0.03 + 0.02 + 0.04 + 0.04 + 0.05 + 0.06 + 0.06 + 0.06 + 0.07 + 0.08 + 0.08 + 0.08 + 0.07 + 0.07 + 0.05 + 0.05 + 0.04 + 0.03 + 0.01 + 0.01 + 0.00 = 1
F(230) - F(228) / (230 - 228) = (1 - 0.99) / (230 - 228) = 0.01/ 2 = 0.0055 = f(229)
f(x) = f(210) + f(211) + f(212) + f(213) + f(214) + f(215) + f(216) + f(217) + f(218) + f(219) + f(220) + f(221) + f(222) + f(223) + f(224) + f(225) + f(226) + f(227) + f(228) + f(229) + f(230) = 1
P(210 < x < 230) = F(230) - F(210) + P(230)= 1 - 0.03 + 0.00 = 0.97