Marimi ale corelatiei la nivel nominal

MARIMI ALE CORELATIEI LA NIVEL NOMINAL

Cele mai utilizate marimi ale corelatiei dintre variabile masurate la nivel nominal sunt coeficientul φ, coeficientul de contingenta C, coeficientul V al lui Cramer si coeficientul λ.

Coeficientii φ, C si V sunt marimi ale corelatiei bazate pe χ². Coeficientul φ se calculeaza cu ajutorul urmatoarei formule:

Formula 1

Sa consideram din nou tabelul 10.1, in care se prezentau datele (fictive) ale unui studiu privind sexul si dominanta functional-operativa a mainilor, reprodus aici ca tabelul 5.

Tabelul 5 Sexul si dominanta functional operativa a mainilor

Dupa cum am constatat prin aplicarea testului χ², relatia dintre cele doua variabile este statistic semnificativa, i.e valoarea χ² (obtinut) = 18 s-a dovedit a fi semnificativa la un nivel de incredere de 95%. Ceea ce ne intereseaza acum este taria corelatiei. Aplicand formula 1, obtinem:

Valoarea φ = 0,42 indica o corelatie cel mult moderata intre sex si dominanta functional-operativa a mainilor. Relatia dintre aceste variabile este statistic semnificativa (χ²), dar nu este puternica. Problema este ca φ ia valori cuprinse intre 0 (nici o corelatie) si 1 (corelatie perfecta) numai pentru tabele 2 2. Pentru tabelele de mare dimensiune, φ poate depasi valoarea 1, ceea ce face ca interpretarea acestui coeficient sa devina problematica. Oricum, dupa cum vom vedea, valoarea lui φ obtinuta pentru exemplul de mai sus este foarte apropiata de valorile obtinute prin calcularea celorlalti coeficienti de corelatie mentionati.

Coeficientul C se calculeaza cu ajutorul urmatoarei formule:

Formula 2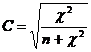

Aplicand aceasta formula la datele din tabelul 5, obtinem:

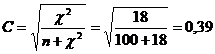
Deficienta coeficientului C este aceea ca, fiind o marime subunitara, nu poate lua niciodata valoarea 1. Se demonstreaza ca pe masura ce dimensiunea tabelului creste, C tinde catre 1. De pilda, valoarea maxima a lui C este 0,82 pentru un tabel 3 3 si 0,87 pentru un tabel 4 4. De aceea, se recomanda folosirea acestui coeficient numai pentru tabele de mare dimensiune (aproximativ de la 10 linii sau/si coloane in sus).

Coeficientul V se calculeaza cu ajutorul urmatoarei formule:

Formula 3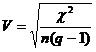

in care q este cea mai mica dintre valorile numerice r (numar de randuri) si c (numar de coloane) pentru tabelul respectiv. Aplicand formula 3 la datele din tabelul 5 obtinem:

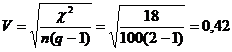
Dupa cum se poate constata, rezultatul obtinut prin calcularea coeficientului V este acelasi cu cel obtinut prin calcularea coeficientului φ. Coeficientul V are valoarea maxima 1, dar numai pentru tabele mai mari de 2 2.

Cu toate deficientele lor, intrucat sunt usor de calculat, coeficientii φ, C si V pot fi folositi in calitate de primi indici ai importantei unei corelatii.

In situatii de cercetare mai pretentioase se obisnuieste sa se utilizeze coeficientul λ., care ia valori cuprinse intre 0 si 1. In cazul in care nu se doreste sau nu se poate identifica variabila independenta, se foloseste varianta simetrica a coeficientului λ, a carui formula de calcul este urmatoarea:

Formula 4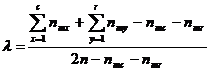

in care n_mx = cea mai mare frecventa in coloana x

n_my = cea mai mare frecventa in randul y

n_mc = cel mai mare marginal de coloana

n_mr = cel mai mare marginal de rand

Sa presupunem ca intr-o cercetare privind relatia dintre apartenenta religioasa si atitudinea fata de pedeapsa capitala s-au obtinut rezultatele din tabelul 6.

Tabelul 6 Apartenenta religioasa si atitudinea

fata de pedeapsa capitala

Pentru datele din acest tabel avem:

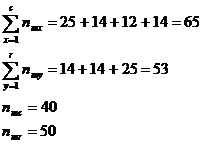
Aplicand formula 4, obtinem:

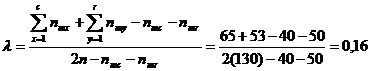
Daca se poate identifica variabila independenta, atunci se foloseste varianta asimetrica a coeficientului λ, notat λ_y, a carui formula de calcul este urmatoarea:

Formula 5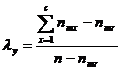

Considerand exemplul de mai sus, daca cercetatorul identifica drept variabila independenta apartenenta religioasa, atunci se obtine:

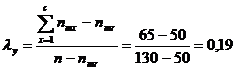
Pentru cele mai multe situatii de cercetare, interpretarea celor doua variante ale coeficientului λ este similara interpretarii coeficientilor C si V. Pentru exemplul considerat aici, putem conchide ca cele doua variabile sunt corelate, dar ca aceasta corelatie este foarte slaba[1].