ANOVA PENTRU O VARIABILA INDEPENDENTA

Inainte de a trece la expunerea testului ANOVA pentru o variabila independenta sa notam ca intr-un experiment psihologic, cercetatorul manipuleaza cel putin o variabila si inregistreaza raspunsurile subiectilor in privinta unei alte variabile, cu scopul de a constata eventualul efect al primei variabile asupra celei de-a doua. De pilda, cercetatorul poate expune un grup de subiecti unor conditii de stres si un alt grup unor conditii normale, pentru a constata daca stresul influenteaza indeplinirea unei anumite sarcini. Variabila manipulata este numita variabila independenta, iar variabila care este observata si masurata este numita variabila dependenta.

Un cercetator presupune ca subiectii supusi unui interviu vor furniza cu atat mai multe informatii cu caracter personal, cu cat se afla mai aproape de intervievator. Pentru a verifica aceasta presupunere, cercetatorul monteaza un experiment la care participa 15 subiecti. Fiecare subiect primeste aceleasi intrebari de la acelasi intervievator. Variabila independenta (A) este distanta fata de intervievator, cu urmatoarele categorii: mica (0,5 metri), medie (1,5 metri), mare (2 metri). Pentru a fi intervievati, subiectii sunt repartizati aleatoriu intr-una dintre cele trei categorii ale variabilei independente. Variabila dependenta (B) este numarul de raspunsuri cu caracter personal date de subiect. Datele obtinute, impreuna cu marimile necesare pentru ANOVA sunt prezentate in urmatorul tabel:

Tabelul 1 Calcule initiale pentru ANOVA, o variabila independenta

Pentru fiecare grup i, T_i este totalul scorurilor individuale, n_i este numarul de subiecti, este media aritmetica a scorurilor, Σ este suma patratelor scorurilor individuale, iar este patratul totalului scorurilor. De notat ca grupurile obtinute sunt independente, precum si ca formulele de calcul care urmeaza sunt aplicabile si in cazul in care este vorba despre un numar diferit de subiecti in fiecare grup.

In ANOVA pentru o variabila independenta se considera doua surse de variatie: (i) variatia mediilor aritmetice ale grupurilor si (ii) variatia datorata diferentelor dintre subiectii din fiecare grup, care poate fi atribuita procesului de esantionare. Pentru inceput, se calculeaza trei sume de patrate ale abaterilor fata de medie sau, pe scurt, sume de patrate. Vom desemna generic prin SS aceste sume de patrate[1]: (1) SS_TOTAL - suma patratelor abaterilor fiecarui scor individual fata de media aritmetica a tuturor scorurilor, numita si marea medie; (2) SS_A - suma patratelor abaterilor fiecarei medii de grup fata de marea medie; (3) SS_EROARE - suma patratelor abaterilor fiecarui scor individual fata de media aritmetica a grupului respectiv. Litera "A" din SS_A arata ca lucram cu varianta sistematica a variabilei independente A. SS_A reflecta prima sursa de variatie, iar SS_EROARE pe cea de-a doua.

Putem calcula aceste abateri direct pe baza datelor din tabel. Intrucat astfel de calcule sunt greoaie, vom utiliza formule simplificate.

Formula 1 

in care Σ= suma patratelor scorurilor individuale ale tuturor subiectilor din

experiment = Σ + Σ + Σ

= patratul totalului tuturor scorurilor =

N = numarul total de subiecti din experiment.

Daca se efectueaza calculele pe hartie sau cu un calculator de buzunar, este convenabil sa se afle mai intai Σ pentru scorurile din fiecare grup, asa cum am facut in tabelul de mai sus, dupa care sa se adune aceste sume. Aplicam formula 1:

Atunci cand calculam SS_TOTAL este recomandabil sa retinem termenii diferentei, 8545 si 7752,07, pe care ii vom folosi pentru simplificarea calculelor ulterioare.

Odata de am calculat SS_TOTAL, putem calcula SS_A dupa urmatoarea formula:

Formula 2

In aceasta formula, T_i este un simbol general pentru T₁, T₂ si T₃, iar n_i este un simbol general pentru n₁, n₂ si n₃. Astfel, odata ce cantitatea este calculata pentru fiecare grup, cantitatile sunt adunate, dupa cum arata simbolul Σ. Sa notam ca a doua parte a formulei 2, G²/N, a fost deja calculata, atunci cand am obtinut SS_TOTAL, asa incat vom prelua direct rezultatul respectiv in calculul SS_A:

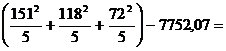
Si aici vom retine unul dintre termenii diferentei, si anume 8381,80, pe care il vom folosi pentru calculul SS_EROARE, dupa urmatoarea formula:

Formula 3

Ambele cantitati cerute de aceasta formula au fost calculate anterior, cand am obtinut SS_TOTAL si, respectiv, SS_A, asa incat vom prelua direct rezultatele respective in calculul SS_EROARE:

De notat ca SS_TOTAL = SS_A + SS_EROARE. Aceasta relatie poate fi utilizata pentru a controla corectitudinea calculelor.

Pasul urmator in calculul ANOVA consta in calcularea a doua medii aritmetice ale sumelor de patrate ale abaterilor fata de medie sau, pe scurt, medii aritmetice ale sumelor de patrate. Vom desemna generic prin MS aceste medii[2]: (1) MS_A - media aritmetica pentru SS_A, numita varianta sistematica si (2) MS_EROARE - media aritmetica pentru SS_EROARE, numita varianta de eroare.

Formula 4

In aceasta formula, k este numarul de grupuri, k 1 fiind numarul de grade de libertate asociate SS_A, pe care il vom nota in continuare cu gl_A.

Formula 5

Aici, N k reprezinta numarul de grade de libertate asociate SS_EROARE, pe care il vom nota in continuare cu gl_EROARE.

Distributia de esantionare in ANOVA este distributia F (numita astfel in onoarea britanicului Ronald Fisher (1890-1962), biolog si statistician, inventatorul ANOVA). Forma aproximativa a unei curbe F este urmatoarea:

Figura 1 Un exemplu de curba F

Forma exacta a unei curbe F depinde de valorile pentru gl_A si, respectiv, pentru gl_EROARE. De notat ca folosirea distributiei F cere ca variabila dependenta sa fie normal distribuita in cele k populatii si ca aceste populatii sa fie egal dispersate[3]. In tabelul distributiei F (vezi Anexa D) in prima coloana din stanga sunt trecute gradele de libertate pentru MS_EROARE (gl_EROARE = N - k), de la 1 la 120 si . Pe cea de-a doua coloana din stanga apar nivelele α. Pe primul rand al tabelului apar gradele de libertate pentru MS_A (gl_A = k - 1), de la 1 la 120 si

Figura 2 Schema tabelului valorilor critice ale distributiei F

La intersectia randului pentru N - k grade de libertate si nivelul α ales cu coloana pentru k - 1 grade de libertate se gaseste F (critic), adica valoarea care marcheaza inceputul zonei critice in distributia F. In exemplul nostru, pentru N - k = 12 si k - 1 = 2, alegand un nivel α = 0,05, F (critic) = 3,8853 sau, rotunjit, 3,8 Valoarea pentru F (obtinut) se calculeaza cu formula urmatoare:

Formula 6

Daca intervin doar factori intamplatori, valoarea asteptata pentru F (obtinut) este 1,0. Cu cat este mai mare valoarea pentru F (obtinut), cu atat este mai mica probabilitatea ca rezultatele experimentului sa se datoreze intamplarii. Regula de decizie este urmatoarea:

Se respinge H₀, daca F (obtinut) > F (critic)

In exemplul nostru,

Intrucat F (obtinut) cade in zona critica (23,15 > 3,89), vom conchide ca rezultatele experimentului sunt semnificative si vom respinge ipoteza ca mediile aritmetice sunt egale la nivelul populatiei.

In termenii modelului in patru pasi, testul ANOVA pentru o variabila independenta, in exemplul nostru, decurge dupa cum urmeaza:

Pasul 1. Enuntarea ipotezelor

H₀: μ₁ = μ₂ = μ₃

H_a: Cel putin o medie aritmetica difera de celelalte

Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice

Distributia de esantionare = Distributia F

α = 0,05

gl_EROARE = N - k = 12

gl_A = k - 1 = 2

F(critic) = 3,89

Pasul 3. Calcularea statisticii testului

Organizarea calculului ANOVA se face cu ajutorul unui tabel de calcule initiale (v. tabelul 1), precum si al unui tabel ANOVA rezumativ, numit tabel al surselor de variatie. Forma generala a unui astfel de tabel este urmatoarea:

In exemplul nostru, avem urmatorul tabel:

Tabelul 2 ANOVA rezumativ, o variabila independenta

Pasul 4. Luarea deciziei

Intrucat, F (obtinut) cade in zona critica (23,15 > 3,89), ipoteza de nul este respinsa. La nivelul populatiei, mediile aritmetice ale scorurilor corespunzatoare celor trei distante difera semnificativ. Enuntul de probabilitate asociat acestei concluzii este urmatorul: probabilitatea ca diferenta observata intre mediile aritmetice ale grupurilor sa apara din intamplare, daca H₀ ar fi in realitate adevarata, este mai mica de 0,05.

De notat ca in cazul in care se considera mai mult de doua categorii ale variabilei independente (ca in exemplul nostru in care avem trei grupuri), F (obtinut) nu arata care este grupul care difera semnificativ de celelalte. O modalitate de a examina diferenta dintre doua grupuri este de a utiliza formula SS_A pentru a calcula suma patratelor si media sumei de patrate pentru cele doua grupuri (numarul de grade de libertate in acest caz fiind 2 - 1) si de a utiliza cantitatea MS_EROARE, calculata anterior, ca eroare de varianta pentru calcularea F (obtinut). Au fost dezvoltate si metode mai sofisticate pentru a evalua diferenta dintre doua grupuri, dupa ce s-a determinat un F (obtinut) semnificativ, numite teste de comparare multipla post hoc, precum si metode de testare a unor ipoteze specifice privind diferentele dintre medii, numite comparatii a priori sau comparatii planificate[4].