Indici statistici de start

Indici statistici de start

1.     Determinarea valorii centrale (a tendintei centrale)

a)     Media

- notata cu m sau x

m = x / N

-cand facem media a doua subgrupuri diferite, se aplica formula medie ponderate (m_p)

m_p= ;

Exemplu:

m1=6; N1=10; m2=7; N2=20;

m_p= ;

Daca grupam datele, obtinem urmatorul tabel:

X X_K f f * X_K

3 - 5 4 3 12

6 - 8 7 5 35

9 - 11 10 9 90

12 - 14 13 16 208

15 - 17 16 10 160

18 - 20 19 4 76

21 - 23 22 3 66

24 - 26 25 1 25

In acest caz, putem calcula media dupa formula

m = T / N;

b) Mediana - cand avem distributie asimetrica si este acea valoare care imparte sirul ordonat (crescator sau descrescator) in doua parti egale.

se noteaza cu Med;

se gaseste exact la mijlocul sirului

locul sau rangul pe care-l ocupa mediana se calculeaza dupa formula: ;

Exemplul 1: 4 4 5 6 6 7 7 7 7 8 9

Locul =6 Med = 7.

Exemplul 2: Fie valorile ordonate:

3       4 4 5 6 7 7 8 8 9

Loc = 5.5; Med = 6.5;

Daca vrem sa calculam mediana pe datele grupate din tabelul de mai sus, aplicam aceeasi formula de calcul, dar se aplica, pentru calcularea locului, formula N / 2.

In exemplul dat, N / 2 = 51 / 2 = 25.5 se afla in clasa 12 - 14.

Avand in vedere ca variabila se considera continua si nu discreta, limitele exacte ale intervalului 12 - 14, se considera 11.5 - 14.5, iar formula de calcul a medianei este:

Med = l+ , unde: l = limita inferioara a intervalului;

F_s = totalul frecventelor situate sub l;

F_i = frecventa corespunzatoare

intervalului localizat;

i = intervalul de grupare;

N = numarul de cazuri.

In cazul nostru:

l = 11.5; F_s = 17; i =3;

N/2 = 25.5; f_I = 16.

Med = 11.5 +

c)Modulul = valoarea care se repeta cel mai des intr-un sir de rezultate.

2.     Variabilitatea, omogenitatea datelor

. Dispersia (s² sau s²) - se mai numeste varianta.

s²= s² = a(x-m²) / (N-1), unde x = fiecare valoare;

m = media.

. Abaterea standard (s

s =

Expresia a(x-m)² se numeste suma produselor si mai poate fi calculata si prin formula: ax² - T² / N, in care T = ax.

Exemplu:

Note (x)                   f f * x (f * x)*x

3 2 6 18

4 2 8 32

5 3 15 75

6 7 42 252

7 10 70 490

8 8 64 512

9 4 36 324

10 2 20 200

N=38; T=261; ax²= 1903.

Formula este , pentru acest caz, s²= 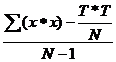s²=3.

. Formula computationala:

s²= s² = ;

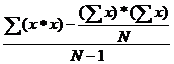Exemplu:

X: 5 4 4 6 6 ;

Y:25 16 16 36 36;

aX = 25; a(X*X) = 129;

s² = 1.

Prin s si s² putem aprecia gradul de omogenitate al grupului.

. Exista un coeficient de variatie PIERSON, cu ajutorul caruia nu facem comparatie intre doua grupuri, ci intre doua fenomene.

V = , unde V= coeficientul de variatie (numit si

variabilitate).

Cand: VI [0%;15%], imprastierea este mica si media este reprezentativa;

VI[15%;30%], imprastierea este mijlocie si media este suficient de

reprezentativa;

V>30%,33%, media nu este reprezentativa (din cauza

omogenitatii).

3.     Semnificatia abaterii standard

Intr-o distributie normala in intervalul [m 3s] sunt dispuse toate valorile.

Avand s, putem afla departarea fata de mesie.

Retine!!!

1)     s masoara distanta la care se afla o cota oarecare in raport cu media;

2)     s poate deveni o masura a variabilitatii.

I.        Inferenta statistica

1.     Proprietatile distributiei normale

Extragerea din populatie a unui esantion;

Supunerea esantionului la o anumita experienta;

Prelucrarea datelor;

Extrapolarea datelor de la esantion la populatie.

Pentru a vedea in ce masura datele obtinute pe esantion sunt relevante pentru populatie se recurge la inferenta statistica.

Distributia normala - s-a demonstrat ca s poate sa ne indice imprastierea datelor in jurul mediei. In acest sens, 1.96 s cuprind 95% din aria de sub curba (asadar raman 2.5 procente in stanga, respectiv in dreapta).

2.58 s acopera 99% din suprafata.

Atunci cand vrem sa lucram cu o unitate de masura standard, lucram cu variabile normate z.

z = , unde x = cota, valoarea obtinuta la test;

m = media valorilor obtinute la test.

Pe baza acestei distributii standard, se ajunge - prin calcul - la urmatoarele formule:

m 1.96 s 95% p = 0.05 sau p = .05 unde p = grad de

incredere. m 2.58 s 99% p = 0.01 sau p = .01

2.     Probleme de estimare

Practic, in cele demonstrate mai sus, s-a pus problema intervalului de incredere.

Semnificatia unei medii

Media este mai semnificativa in functie de:

volumul esantionului studiat;

variabilitatea populatiei.

Eroarea standard a mediei (E) se calculeaza dupa formula:

E = ;

Pe aceasta baza, se poate evalua greseala pe care o facem, luand drept baza media esantionului, in loc de media populatiei. Tot pe aceasta baza se stabilesc si limitele intre care se afla, cu o anumita probabilitate (grad de incredere), adevarata valoare m a colectivitatii generale.

. (m - 1.96 E, m +1.96 E) se numeste interval de incredere la p=.05 (deci exista numai 5% sanse de a gresi);

. (m - 2.58 E, m+ 2.58E) reprezinta intervalul de incredere la p=.01;

Atunci cand se lucreaza cu frecvente, eroarea (E) este:

E = .

Exemplu: Intr-o statistica a erorilor la casierie s-au constatat 134 de erori in plus si 289 erori in minus (in total, 423 erori)

Pentru erorile in plus: f = E== 0.02;

Limitele de incredere: f E.

Pentru p = 0.05, avem f 1.96E.

Pentru p = 0.01, avem f 2.58E.

3.     Sarcini si probleme de comparatie

Se aplica teste / probe unor esantioane si se calculeaza indicii de start (de exemplu, media). Care este gradul de semnificatie al diferentelor? Sau de la ce nivel de incredere diferentele pot fi considerate semnificative?

. Ipoteza specifica (Hs) = ipoteza psihologica sau pedagogica ce sta la baza experientei respective.

. Ipoteza nula (Ho) nu metoda duce la rezultate mai bune, ci intamplarea.

Noi va trebui sa calculam un prag de semnificatie care indica, de fapt, riscul pe care ni-l asumam. Daca probabilitatea obtinerii acestor rezultate este mai mica de 0.05, de exemplu, respingem ipoteza nula (sau ipoteza hazardului) si spunem ca rezultatele se datoreaza ipotezei specifice.

. p < 0.10 ultimul caz acceptat in psihologie;

. p > 0.10 nu mai este de incredere;

Cercetarea este buna daca p = 0.05 si este foarte buna daca p = 0.01.

Ipoteza nula este o ipoteza statistica precisa, pe cand ipoteza specifica este imprecisa (pentru ca lucram cu o anumite improbabilitati).

Daca ipoteza nula este infirmata, atunci acceptam ipoteza specifica.

Daca ipoteza nula nu este infirmata, se considera suspendarea deciziei, in sensul ca datele noastre nu sunt suficiente (retestez).

Pentru a vedea daca anumite diferente sunt semnificative, se aplica o serie de calcule, de formule, care se numesc criterii (z, t, l², etc) si se compara cu anumite valori standard existente in tabele. Daca valoarea calculata de noi este mai mare sau egala cu valoarea critica existenta in tabele, probabilitatea asociata este mai mica sau egala cu pragul a (0.01; 0.05; 0.1) si se decide respingerea ipotezei nule (Ho).

Daca valoarea calculata de noi este mai mica decat valoarea gasita in tabele, inseamna ca probabilitatea este mai mare decat 0.10 si respingem ipoteza specifica.

Esantioane perechi (corelate) - fie acelasi esantion supus unor testari succesive, fie esantioane stabilite astfel incat pentru variabilele semnificative asociate cu ipoteza noastra, fiecarui element din esantion experimental trebui sa-i corespunda un element similar in esantionul de control.

Esantioane independente - cand comparam doua esantioane stabilite la intamplare.

4.     Semnificatia diferentei intre doua medii in cazul

esantioanelor independente

Sunt doua cazuri:

N 30 se aplica criteriul z;

N < 30 se aplica criteriul t;

Se accepta faptul ca de la 30 de subiecti in sus distributia tinde sa fie normala.

Criteriul z

;

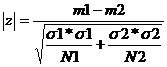Exemplu:

m1 = 7.7;                        m2 = 6.7;

N1 = 33;                          N2 = 34;

s²₁ = 3.15; s²₂ = 3.5;

Aplicam formula si obtinem: 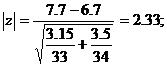p=0.02

Daca probabilitatea ce corespunde indicelui z este mai mare decat 1.96, atunci diferenta dintre cele doua medii este semnificativa la p<0.05.

Daca z calculat este mai mare decat 2.58, atunci diferenta este semnificativa la pragul p < 0.01.

Daca z calculat ste mai mic decat 1.96, respingem ipoteza specifica.

Criteriul t

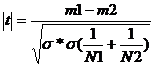, unde s²=;

N1+N2 - 2 = n (numarul gradelor de libertate).

Exemplu:

m1 = 13.3; m2 = 14.2;

N1 = 10; N2 = 10;

a(x-m1)² = 82.1; a(x-m2)² = 97.6;

s²=;

gradul de libertate = 18;

Semnificatia diferentelor intre medii in cazul

esantioanelor perechi

In cazul esantioanelor perechi, presupunem ca avem aceeasi subiecti .

Subiecti Note trimestrul I Note trimestrul II d d²

A    8 6 2 4

B     7 5 2 4

C     5 5 0 0

D    6 4 2 4

E     5 6 -1 1

F     6 4 2 4

G    6 5 1 1

H    5 4 1 1

I      4 6 -2 4

J      7 5 2 4

K=10                                       Sd=+9 Sd²=27

d= diferenta

Daca facem raportul calculam media diferentelor (md)

md===0,9

Se aplica criteriul pentru esantioane corelate :

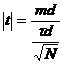
t²_d= ; ;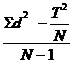

/9=2,1

; gradul de libertate este N-1(adica 9 ).

(vezi tabelul ) diferenta este semnificativa

semnificatia diferentei intre frecvente

CRITERIUL C²

Cand lucram cu frecvente , ne intereseaza atat frecventele observate , cat si cele teoretice .

In general , criteriul 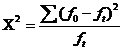, unde f₀ = frecvente observata

F_t= frecventa teoretica

Exemplu :

Presupunem o instalatie comanda - manuala

Accidente?

-automata

Comanda Comandatotal

Manuala automata

Accidentati a25 b23 48

Neaccidentati  c 183 d 112 295

Total208135 343

In acest caz ,

N= numarul gradelor de libertate=(r-1)(c-1). Unde r= nr. de randuri

C= nr. de coloane

In cazul nostru r=2; c=2 deci n=1;

. In cazul in care avem doua grupe, A si B, si avem masuratori, se procedeaza in felul urmator:

x y z Total

A a 63.5 b 20 c 16.5 100

B d 33.7 e 18.3 f 48 100

Total    97.2 38.3 64.5 200

Unde: x - inferior; y - mediu; z - superior.

Sau xI [0,3]; yI[4,6]; zI[7,10].

Pentru frecventa teoretica pentru fiecare celula (a,b,.,f) se inmulteste totalul randului cu totalul coloanei si se imparte la T.

Pentru casuta "a":