
|
|
|
STIINTIFIC
TEHNICI DE SIMULARE
SIMULAREA REPARTITIEI POISSON
Cuvinte cheie
simulare, lambda, repartitie, Metoda Poisson
Introducere
Inceputurile teoriei probabilitatilor sunt legate de numele matematicienilor Blaise Pascal si Pierre Fermat in secolul XVII, ajungand la probleme legate de probabilitate datorita jocurilor de noroc.
Dezvoltarea teoriei probabilitatilor si cercetarea unor probleme nelegate de jocurile de noroc sunt legate de matematicienii: Abraham Moivre, Pierre Simone de Laplace, Carl Friedrich Gauss, Simon-Denis Poisson, Pafnuti Lvovici Cebisev, Andrei Andreevici Markov in secolul XIX, iar in secolul XX Andrei Nikolaevici Kolmogorov si al lui Alexandr Iakovlevici Hincin.
Simularea este o metoda experimental- aplicativa prin care se testeaza un model (sistem) pentru a stabili gradul de adecvare a acestuia in raport cu procesul initial. Simularea se realizeaza prin implementarea sistemului (modelului) pe un dispozitiv de simulare care poate fi specializat sau universal. Este de mentionat dezvoltarea fara precedent a tehnicilor numerice de simulare, care pun la dispozitia cercetatorilor programe dedicate acestei operatii, cu o interfata prietenoasa accesibila chiar si incepatorilor in domeniul informatic.
Cuvantul "simulare" deriva din latinescul "simulatio", care inseamna capacitatea de a reproduce, reprezenta sau imita ceva. In matematica, termenul "simulare" a fost folosit pentru prima data de catre John von
Neumann si S. Ulan in anii 1940-1944, cu ocazia cercetarilor de fizica nucleara efectuate inS.U.A. Ei, impreuna cu N. Metropolis, Fermi si alti matematicieni si fizicieni ai scolii "Los Alamos" au introdus in aceeasi perioada un nume pitoresc in matematica si anume "metoda Monte Carlo". Denumirea, desigur improprie, provine din faptul ca primele metode de generare a numerelor aleatoare au fost cele oferite de rezultatele obtinute la ruletele vestitelor cazinouri din Monte Carlo.
Repartitia Poisson
Este asemanatoare cu cea binomiala, deosebindu-se prin faptul ca n poate fi foarte mare (n-> ∞) si p foarte mic (p->0).
Legea de repartitie: ![]()
Media: a
Dispersia: a
Formula de recurenta: ![]()
Modelul repartitiei Poisson se poate construi pornind de la legea binomiala in
urmatoarele ipoteze [:
p : probabilitatea de aparitie a evenimentului urmarit este mica ;
n : volumul esantionului este suficient de mare astfel incat sa fie indeplinita conditia :
np = λ = constant
Legea lui Poisson mai poarta numele si de legea "evenimentelor rare", dupa
specificul fenomenelor pe care le descrie, evenimente a caror probabiliste de aparitie este redusa.
Functia de repartitie a legii lui Poisson este:
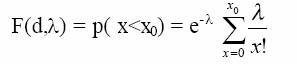
Metoda Poisson
Pi=P(X=i)=![]() i=0,1,2,3,.
i=0,1,2,3,.
M[x]=λ; var[x]=λ;
Variabila aleatoare Poisson de λ reprezinta numarul de evenimente rare (intrarile intr-un sistem de asteptare pe unitatea de timp)
Intervalal de timp dintre 2 sosiri consecutive este o variabila de tip exponential de x.
Pentru generarea lui x generam intervalele de timp τ=intervalele de timp Exp(λ) asfel incat suma lor sa acopere intervalul de timp egal cu unitatea. Numarul j de astfel de intervale este sectiune a variabilei aleatoare de timp Poisson.
j satisface inegalitatea dubla
![]() astfel
il gasim pe j
astfel
il gasim pe j
![]() ui
ui![]() u(0,1)
u(0,1)
Algoritm
Pasul 1 Initializarea algoritmilor RND,Intrare λ,n
Pasul
2: Pentru i=![]() executa
executa
j=-1;P=1
repeta
genereza U![]() U(0,1)
U(0,1)
P=P*u;
j=j+1;
pana cand P<e-λ
retine x=j
Pasul 3 STOP!
Program
//Generarea variabilelor aleatoare de tip Poisson de parametru lambda
#include<iostream.h>
#include<math.h>
#include<time.h>
#include<conio.h>
#include<stdio.h>
#include<stdlib.h>
void main()
cprintf('rn Apasati enter pentru revenire in cpp');
getch();

Bibliografie
1. Purcaru Ion - "Matematici generale si elemente de optimizare", Editura Economica, Bucuresti 1997;
2. Vaduva Ion. - "Modele de simulare cu calculatorul", Editura Tehnica, Bucuresti 1997;
3. Ciucu G., Craiu V., Stefanescu A. - "Statistica matematica si cercetari operationale", vol III, Editura Didactica si Pedagogica , Bucuresti 1978;
4. Dani E., Muresan A. - "Matematici Aplicate in Economie", Universitatea Cluj Napoca, 1988.