|
|
|
POLIGOANE REGULATE
DEFINITIE
Un poligon convex cu toate laturile si toate unghiurile congruente se numeste poligon regulat.
(Exemple cunoscute patratul, triunghiul echilateral.)
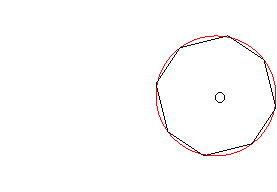Daca printr-un procedeu
oarecare impartim cercul in n arce congruente, si unim succesiv punctele de
diviziune, obtinem un poligon cu n laturi congruente.
Laturile sunt congruentedeoarece subintind arce de cerc de aceeasi masura:
( masura unghiului la centru corespunzator)
Unghiurile poligonului sunt unghiuri
inscrise in cerc care cuprind intre laturi arce de masura:
.
TEOREMA
Orice poligon regulat se poate inscrie intr-un cerc.
DEFINITIE
Segmentul dus din centrul cercului circumscris unui poligon regulat, perpendicular pe latura poligonului, se numeste apotema
CALCULUL ELEMENTELOR IN POLIGOANE REGULATE
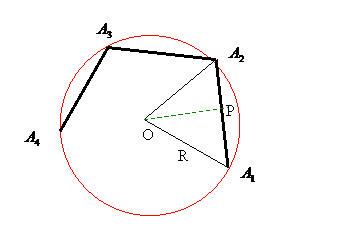Vom calcula latura 
si apotema 
in functie de raza R a
cercului circumscris.
Unghiul la centru corespunzator fiecarei laturi
este:
Triunghiul 
este isoscel.
In
triunghiul 
dreptunghic in P (
, OP apotema) avem:
Aria poligonului este:
Deci
: 
|
|
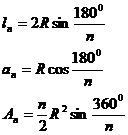
Latura |
Apotema |
Aria |
Perimetrul |
|
Triunghi echilateral |
|
|
|
|
|
Patrat |
|
|
|
|
|
Hexagon regulat |
|
|
|
|
|
|
Inaltimea |
Apotema |
Aria |
Raza |
|
Triunghi echilateral |
|
|
|
|
|
Patrat |
|
|
|
|
|
Hexagon regulat |
|
|
|
|
PROBLEME
Sa se completeze tabelul urmator:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
