Metode de analiza a informatiilor din cercetarile de marketing

1. Metode de analiza univariata

De regula se folosesc pentru:

a)     a se detemina tendintele central a variabilelor considerate;

b)     caracterizarea variatiei si a repartitiei acestora.

Modalitati de determinare a tendintelor centrate a variabilelor considerate

Pentru a determina tendintele central a variabilelor considerate trebuie sa stabilim tipul de scala utilzat.

Daca masurarea variabilelor considerate se realizeaza cu ajutorul scalei nominale indicatorii care exprima tendinta centrala a variabilei considerate este grupul modal sau modulu data de cea mai frecventa aparitie a componentelor esantionului, adica numarul care apare cel mai frecvent intr-un sir.

Un alt indicator al tendintei central este mediana care reprezinta valoarea deasupra si dedesubtul careia se situeaza cate ½ din observatii. Daca datale sunt negrupate in ordine si daca numarul de observatii este fara sot, valoarea median se stabileste fara dificultate (fiind pozitionata la jumatate). Daca datele sunt grupate iar numarul observatiilor este cu sot, mediana se calculeaza astefl: numarul total de observatii se imparte la 2, rezultand numarul observatiilor care trebuie sa fie deasupra si dedesubtul medianei. Apoi se determina frecventele cumulate ale datelor pentru a stabili in care grupa se situaeaza mediana. In fnal se calculeaza valoarea medianei raportand frecventele cumulate ale datelor obtinute din cercetare la grupul cu dimensiunea cea mai mare.

Un alt indicator al tendintei central a variabilelor considerate il reprezinta media aritmetica. Media aritmetica se calculeaza prin insumarea tuturor scorurilor si impartirea rezultatului la numarul de scoruri:

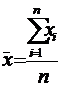
Un ultim indicator este media geometrica dar este destul de rar utilizat in analiza cercetarilor de marketing.

Modalitati de caracterizare a variatiei si a repartitiei variabilelor

Caracterizarea variatiei este un al obiectiv al analizei datelor culese prin cercetarile de marketing. Ea se poate realiza in mod diferentiat, in functie de nivelul de masurare realizat printr-un tip de scala sau altul folosind mai multi indicatori :

a)     distributia de frecventa atat in forma tabelara cat si in forma grafica ;

b)     amplitudinea variatiei care se poate calcula fie ca expresie absoluta, ca diferenta dintre observatia cu valoarea cea mai mare si observatia cu valoarea cea mai mica, fie ca expresie relativa, ca raport dintre amplitudinea observatiei si cea medie.

c)     abaterea absoluta de la medie

2. Modalitati de analiza bivariata

Se folosesc pentru a masura gradul de asociere dintre 2 variabile considerate sub aspectul directiei, intensitatii si semnificatiei statistice. In functie d tipul de scala utilizat, masurarea gradului de asociere dintre variabilele considerate presupune utilizarea mai multor metode.

In cazul scalelor nominale masurarea gradului de asociere dintre variabilele considerate se realizeaza utilizand urmatoarele modalitati.

a)     Intocmirea tabelelor de contingenta. Un asemenea tabel cuprinde distributia de frecvente considerata simultan pe 2 sau mai multe variabile caracterizate.

b)     Folosirea coeficientului de corelatie g _phi care se calculeaza astfel :

g _{phi =,}  unde

a,b,c,d reprezinta frecventele tabelului de contingenta de tipul 2x2 dupa cum urmeaza :

g _phi poate lua valori intre -1,0 si +1,0. Cele 2 extreme indica o asociere perfecta intre variabile, in vreme ce valoarea zero indica lipsa corelatiei. Pentru a determina in ce proportie preferintele pentru factorul investigat sunt explicate de variabilele considerate,  g _phi se ridica la patrat (g _phi² ). Daca  g _phi are o valoare pozitiva acest lucru indica o corelatie pozitiva in sensul ca exista in ansamblu o asociere intre variabilele considerate pentru factorul studiat.

Pentru testarea gradului de semnificatie a asocierii dintre opiniile subiectilor constituiti in doua esantioane distincte si preferinta pentru factorul (produsul) cercetat se poate utiliza testul neparametric c²

Testul lui  χ²

Etapele de lucru, in cazul acestei metode, sunt:

a)     se efectueaza un sondaj asupra colectivitatii generale, pentru a obtine valorile lui x si y;

b)     se inregistreaza valorile lui x si y in tabelul de contingenta;

c)     pe baza ipotezei nule, respectiv pe baza presupunerii ca nu exista legatura intre variabilele x_i si y, se vor calcula valorile teoretice pe care le notam cu A_ij, pe baza relatiei:

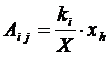
pentru , iar

d) se masoara diferenta dintre valorile observate si cele calculate pe baza ipotezei nule; valoarea calculata a lui χ² va fi:

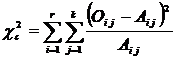, unde:

r si k - numarul de randuri, respectiv de coloane ale tabelului de contingenta;

O_ij - frecventele randului i si ale coloanei j, care rezulta din observare;

A_ij - frecventele randului i si ale coloanei j, care se asteapta sa rezulte conform ipotezei nule.

Valoarea lui χ² are o anumita distributie de probabilitate, data de tabelul lui Fischer, care cuprinde valorile lui χ² pentru anumite grade de libertate si anumite probabilitati, precum  si numarul gradelor de libertate: g = (r-1) (k-1).

Daca >ipoteza nula se respinge, iar

Daca <, ipoteza nula se accepta.

3. Tehnici de analiza multivariata

In cercetarile de marketing se intalnesc foarte frecvent situatii in care sunt supuse analizei mai mult de 2 variabile. Este vorba de analiza multivariata care presupune utilizarea unui grup de metode statistico-matematice cu ajutorul carora se pot cerceta simultan legaturile de asociere existente intre 3 sau mai multe variabile.

Cele mai cunoscute metode de analiza multivariata sunt :

a)     metodele de regresie multipla ;

b)     metoda discriminantului liniar multiplu ;

c)     metoda multivariata a variatiei ;

d)     metoda canonica;

e)     metoda factoriala;

f)      analiza grupurilor;

g)     scalarea multidimensionala in varianta metrica sau nemetrica;

h)     analiza structurilor latente.

a) Metoda regresiei multiple

In principal, in cadrul metodei se urmaresc urmatoarele aspecte:

determinarea proportiei in care variatiile variabilei dependente pot fi explicate prin variatiile variabilelor independente, atat in ansamblul lor, cat si separat sau pe grupe de variabile.

evaluarea gradului de interdependenta dintre variabilele independente. Cu cat numarul de variabile independente este mai mare si cu cat relatia dintre variabilele independente este mai mare, cu atat este de dorit a se elimina una sau mai multe dintre ele in analiza regresiei, pentru ca, in acest caz, de regula, numai o variabila independenta are un impact semnificativ asupra relatiei dintre variabilele independente si cele dependente.

Un model regresional multiplu se prezinta sub forma urmatoarei ecuatii:

unde:

Y- valoarea estimata a variabilei dependente y (uneori se foloseste denumirea de valoare calculata si se noteaza cu Y_c);

- parametru care reprezinta valoarea estimata a interceptului;

- valoarea estimata a parametrilor care exprima relatia dintre Y si Xi;

X_i - variabile independente;

n - numarul variabilelor independente.

b) Metoda discriminatului liniar multiplu

Este o metoda de estimare a relatiei liniare dintre o variabila dependenta de tip dihotomic (cu 2 stari) sau multidihiotomic (cu mai mult de 2 stari) si combinatii liniare ale mai multor variabile independente pentru masurarea carora s-a folosit o scala metrica.

Folosirea acestei metode presupune urmatoarele etape :

definirea apriorica a grupurilor variabilelor dependente si a starilor posibile ale variabilelor dependente (cumparatori, necumparatori).

definirea variabilelor independente presupuse a fi utilizate in realizarea discriminarii intre grupurile respective.

Metoda discriminantului liniar multiplu urmareste delimitarea celor 2 grupuri, astfel incat ele sa fie cat mai omogene in interior si cat mai eterogene unele fata de altele.

c) Analiza multivariata a variatiei

Cuprinde un grup de metode apartinand statistici inferentiale utilizate mai ales pentru analiza datelor provenite din diferite tipuri de experimente, cu ajutorul carora se poate face separarea si testarea semnificatiei efectelor cauzate de actiunea simultana a mai multor factori. Concret este vorba de urmatoarele metode : proiectarile factoriale; patratele latine; patratele greco-romane. Indiferent de metoda folosita pentru analiza variatiei, datele trebuie sa indeplineasca urmatoarele cerinte :

se presupune ca datele culese sa provina de la grupuri experimentale a caror constituire s-a facut aleator ;

se presupune ca setul de date utilizate pentru a calcula variatia aleatoare respectiv eroarea experimentala poate sa prezinte o abatere standard ;

se presupune ca variatia aleatoare este independenta de la o observatie la alta;

se presupune ca efectele diferitelor surse ale variatiei, respectiv: efectele factorilor experimentali, efectele de interactiune dintre factori si eroarea experimentala sunt aditive si nu multiplicative.

d) Analiza canonica

Este o alta metoda statistica multivariata de studiere a relatiei liniare intre 2 grupuri de variabile dependente si un grup de variabile independente si unele si altele putand fi masurate cu ajutorul unos scale metrice sau nemetrice.

Obiective:

determinarea directiei, intensitatii si semnificatiei corelatiei dintre cele 2 seturi de variabile considerate;

estimarea coeficientilor celor 2 seturi de variabile pentru numeroasele combinatii liniare care se pot realiza si identificarea combinatiei care maximizeaza corelatia intre seturi;

explicarea si previziunea variatiei setului de variabile dependente avand la baza covariatia lor cu variabilele independente;

determinarea contributiei relative a fiecarei variabile in cadrul functiilor canonice si identificarea variabilelor care contribuie cel mai mult la explicarea asocierii seturilor.

e) Analiza factoriala

Are ca scop cercetarea legaturilor de interdependenta dintre mai multe variabile cu ajutorul carora se caracterizeaza un anumit fenomen, prin condensarea (reducerea) volumului datelor cuprinse in variabilel initiale si constituirea unui set mai mic de factori urmarindu-se o pierdere minima de informatii. La baza analizei factoriale sta urmatoarea ipoteza: daca in cadrul setului variabilelor supuse cercetarii exista o interdependenta sistematica, ele trebuie sa posede cateva elemente latente comune care poarta denumirea de factori.

Obiective:

identificarea setului de dimensiuni latente existente in variabilele initiale;

combinarea (sau condensarea) componentelor unei populatii statistice si crearea unor grupuri distincte;

identificarea variabilelor corespunzatoare, pornind de la setul initial si crearea unui nou set, mai redus, care urmeaza a fi supus in continuare,analizei cu ajutorul regresiei, corelatiei sau discriminantului liniar multiplu.

f) Analiza grupurilor

In principiu exista 2 strategii de analiza a grupurilor:

una care pleaca de la intrega multime ce urmeaza sa fie subdivizata in grupuri omogene;

alta care pleaca de le fiecare componenta din cadrul multimii, constituierea grupurilor facandu-se prin adaugare succesiva la o anumita componenta a altor componente cu care se aseamana cel mai mult din punct de vedere al criteriului utilizat.

g) Scalarea multidimensionala

Reprezinta un proces in care cu ajutorul diferitelor tehnici, obiectele sau fenomenele analizate sunt prezentate sub forma de puncte intr-un spatiu perceptual multidimensional ale carui dimensiuni sunt interpretate ca atribute cu ajutorul carora obievtele sau fenomenele sunt diferentiate unele de altele.

O caracteristica importanta a scalarii multidimensionale si prin care se delimiteaza de scalarea unidimensionala este ca dimensiunile sau atributele nu sunt definite de cercetatori ci sunt generate de subiectii investigati.

Obiective:

determinarea subiectilor in evaluarea obiectivelor sau fenomenelor;

estimarea importantei relative a acestor atribute si a relatiilor perceptuale dintre ele