Teorema energiei electromagnetice. fluxul de energie electromagnetica. vectorul lui poynting.

teorema energiei electromagnetice. Fluxul de energie electromagnetica. vectorul lui poynting.

Plecand de la ecuatiile lui Maxwell, se pot stabili unele rezultate importante privind bilantul energiei in camp electromagnetic.

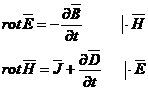
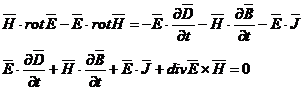
Se integreaza aceasta relatie pentru un domeniu v_Σ limitat de o suprafata inchisa oarecare Σ, in interiorul careia se presupune ca se gasesc medii liniare, izotrope si fara campuri imprimate. Aplicand ultimului termen transformarea Gauss-Ostrogradski

rezulta:

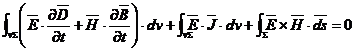                           (1)

Se analizeaza semnificatiile diferitilor termeni ce intervin in relatie:

- reprezinta puterea din unitatea de volum care apare sub forma de

caldura (efectul Joule-Lenz). Pentru intregul volum aceasta putere va fi:

- reprezinta densitatea de volum a energiei electrice

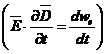. Pentru intregul volum aceasta putere va fi:

.

Daca mediul este liniar , expresia densitatii de volum a energiei electrice devine: iar pentru intregul volum

- reprezinta densitatea de volum a energiei campului

magnetic 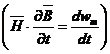. Daca ne referim la intregul volum aceasta putere va fi: .

In cazul particular al mediilor liniare, iar pentru intregul volum

expresia se numeste vectorul lui Poynting. Aceasta marime releva

existenta unei puteri electromagnetice care se transmite prin suprafata Σ ce margineste domeniul considerat (din interior spre exterior sau invers). Puterea electromagnetica transmisa prin suprafata Σ este:

deci apare sub forma fluxului vectorului lui Poynting prin suprafata respectiva. Aceasta putere se mai numeste si flux de energie electromagnetica in unitatea de timp.

Valoarea numerica a vectorului lui Poynting reprezinta energia electromagnetica care strabate in unitatea de timp unitatea de suprafata, respectiv puterea electromagnetica care se transmite prin unitatea de suprafata (W m²), iar orientarea acestui vector indica directia si sensul de propagare a energiei electromagnetice. Vectorul lui Poynting este diferit de zero numai in punctele in care exista simultan marimile de stare si , iar vectorii respectivi nu sunt paraleli. Rezulta ca vectorul este perpendicular pe planul definit de vectorii si .

Relatia (1) poate fi scrisa sub forma:

sau:      (2)

unde

Relatia (2) poarta denumirea de teorema energiei electromagnetice in forma integrala, care se enunta astfel: derivata in raport cu timpul luata cu semn schimbat a energiei campului electromagnetic din volumul considerat este egala cu suma dintre puterea P_J care apare sub forma de caldura in procesul de conductie si puterea electromagnetica P_S transmisa prin suprafata ce margineste volumul respectiv.

Observatii: Campul electromagnetic reprezinta inlantuirea reciproca a campurilor electric si magnetic variabile in timp, inlantuire ce se propaga in spatiu sub forma unor unde electromagnetice. Aceste unde sunt purtatoare de energie. Deci, in regim variabil se releva ca un fapt caracteristic existenta unei energii electromagnetice care se propaga in spatiu si timp.

La transportul energiei electromagnetice conductoarele liniei electrice doar dirijeaza propagarea acesteia. La suprafata de separatie conductor-aer vectorul are o componenta tangentiala ce asigura transmisia de energie in lungul liniei spre consumator si o componenta radiala (mult mai mica decat cea tangentiala) corespunzatoare energiei electromagnetice din interiorul conductoarelor liniei, ce se regaseste sub forma de caldura dezvoltata prin efect Joule-Lenz.

Undele electromagnetice se propaga nu numai prin vid (aer) ci si prin corpuri in conditii ce depind de proprietatile fizice de natura electrica si magnetica ale acestora. In cazul mediilor conductoare, patrunderea campului electromagnetic este insotita de scaderea valorii campului de la suprafata inspre interior dupa o lege exponentiala. Caracterizarea fenomenului de patrundere a campului electromagnetic in medii conductoare se face cu ajutorul unei marimi δ numite adancime de patrundere.

unde:   f - frecventa

σ - conductivitatea mediului conductor

μ - permeabilitatea magnetica a acestuia.

In figura este reprezentata variatia densitatii de curent in functie de distanta r de la axa unui conductor cilindric cu raza a, parcurs de curentul i. Fata de regimul stationar, cand J are aceeasi valoare (a), in regim variabil valoarea lui J scade inspre axa conductorului (b). La frecvente foarte inalte curentul obtine o repartitie exclusiv superficiala, densitatea de curent J fiind nula in centrul conductorului. Rezulta ca la frecvente foarte mari se pot folosi conductoare tubulare.

Refularea curentului din axa spre exteriorul conductorului, efect cu atat mai pronuntat cu cat frecventa curentului este mai ridicata, se numeste efect pelicular.

Efectul pelicular are drept rezultat micsorarea sectiunii active a conductorului, ceea ce conduce la marirea rezistentei electrice a acestuia. Prin urmare in curent alternativ rezistenta electrica a unui conductor este mai mare decat in curent continuu,

R_c.a. > R_c.c.

cu atat mai mult cu cat frecventa curentului alternativ este mai mare.