Modelarea si simularea circuitelor de cale fara joante

MODELAREA SI SIMULAREA CIRCUITELOR DE CALE FARA JOANTE

Circuitul de cale  fara joante poate fi considerat ca fiind este o linie multifilara avand doua conductoare active in prezenta solului.

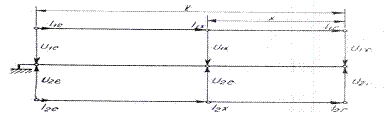
Fig.  III. 1 Circuitul de cale fara joante privit ca linie de transmisie multifilara, cu doua conductoare active in prezenta solului.

Pentru frecventele uzuale de lucru ale circuitului de cale fara joante capacitatile specifice partiale sunt neglijabile. In aceste conditii ecuatiile telegrafistilor de ordinul unu pentru circuitul de cale se prezinta astfel:

Cunoscand constantele de integrare, se pot scrie relatiile ce definesc valorile tensiunilor si curentilor in orice punct al liniei functie de marimile de iesire. Astfel pentru se obtin marimile de intrare:

Aceste relatii pot fi scrise si sub forma matriciala:

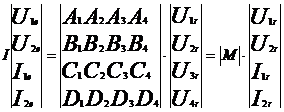
Relatiile de mai sus definesc un hexapol echivalent caii fara joante, caraterizat prin matricea |M|. Matricea |M|, functie de parametrii primari ai liniei si de lungime, stabileste o relatie biunivoca intre marimile de intrare si de iesire din linie, considerata ca hexapol. Dar, practic, nu intereseaza explicit valorile tensiunilor si curentilor in circuitele sina-pamant, ci valorile tensiunilor si curentilor in circuitul format din cele doua sine, la capatul caruia sunt conectate aparatele de emisie si receptie. Apare deci necesitatea determinarii parametrilor unui cuadripol echivalent circuitului de cale fara joante, care sa tina seama de caracterul specific de hexapol al caii.

Determinarea parametrilor cuadripolului echivalent

Schema echivalenta a circuitului de cale fara joante cuprinde hexapolul caii, intre punctul de emisie si cel de receptie, definit prin matricea |M|, admitantele reflectate din circuitul de cale adiacent capatului de receptie Ya, Yb, Yc, respectiv capatului de emisieYA, YB, YC , si aparatajul reprezentat printr-un generator de tensiune de impedanta interna, Ze si impedanta de intrare a receptorului Zr.

Intre punctele 1-1' si 2-2' circuitul de cale fara joante se prezinta ca un cuadripol de parametri A, B, C, D. Determinarea parametrilor presupune stabilirea unei relatii intre marimile de intrare, Ue, Ie, si marimile de iesire Ur, Ir, tinand seama de configuratia circuitului cuprins intre aceste puncte.

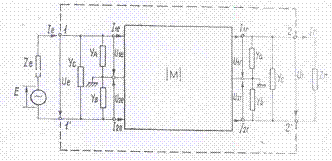
Fig. III.2 Schema echivalenta a circuitului de cale fara joante.

Relatiile de dependenta ce definesc cuadripolul echivalent sunt:

Coeficientii cuadripolului echivalent sunt:

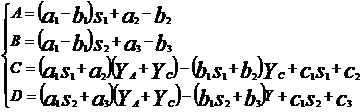
Aceste relatii reprezinta forma cea mai generala a coeficientilor cuadripolului caii, cu ajutorul carora se poate determina comportarea circuitului de cale fara joante in orice situatie existenta in exploatare. Particularizindu-le, de exemplu pentru cazul unui circuit de cale fara joante echilibrat, se obtin coeficientii cuadripolului caii:

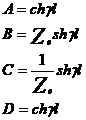
Unde impedanta caracteristica Zc si constanta de propagare γ au expresiile:

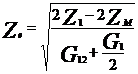
Utilizand cele doua fire ale caii drept conductoare electrice se pot transmite informatii intre blocuri ale instalatiei automatizate, sau prin cuplaj magnetic, catre vehicule, informatii tinand de siguranta circulatiei sau auxiliare (ultima functie fiind practic abandonata pentru instalatii noi).

Pentru studiul circuitelor de cale fara joante izolante ca baza se foloseste teoria generala a circuitelor de cale dar se tine seama de cateva trasaturi specifice conditionate de lipsa joantelor izolante.

Schema generala echivalenta a circuitului de cale fara joante izolante este prezentata in figura de mai jos.

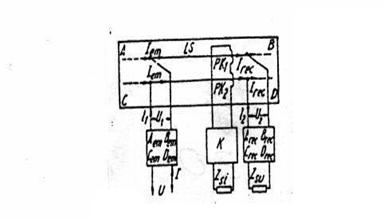
Fig.III. 3 Schema generala echivalenta a circuitului de cale fara joante izolante

Aceasta schema, la fel ca si schema circuitului de cale cu joante izolante este compusa din montajul in cascada a trei cuadripoli: Em, Rec si Ls. Cuadripolii Em si Rec inlocuiesc aparatura respectiva de alimentare si a capetelor de relee, iar cuadripolul Ls inlocuieste linia de cale ferata.

Acest cuadripol se deosebeste substantial de cuadripolul din schema cu joante izolante. Din cauza aceasta, pentru analiza si sinteza circuitelor de cale ferata fara joante izolante, este necesara deducerea ecuatiei pentru calculul coeficientilor cuadripolului, care substituie linia. In circuitele de cale nelimitate preluarea sarcinii se realizeaza atat ca tensiune respectiv curent. In cadrul preluarii sarcinei ca intensitate a curentului, releul de cale intra in functiune in contul fortei electromotoare, introdusa in linii de curenti I, I in bobinele de linie PK1 si PK2, asezate la sine. Pentru circuitele de cale de acest gen, o mare importanta o au problemele legate de asigurarea sensibilitatii la sunt prin aplicarea la circuitul de cale a doua sunturi de tren cu rezistenta diferita in ambele parti ale punctului de conectare a sarcinii.

Schemele de substitutie pentru o linie fara joante, sunt aratate in cazul unor sine de linie bune, in figura nr. III. 4 iar, in cazul intreruperii unui fir in figura III. 5.

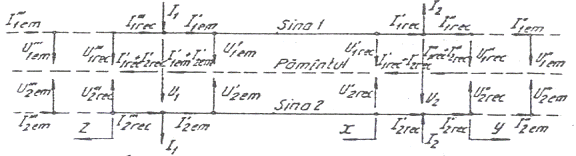
Fig. III. 4 Schema de substituire ( sinele sunt bune)

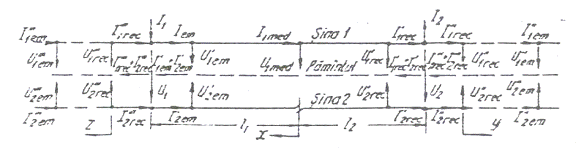
Fig. II.I. 5 Schema de substituire (sina este intrerupta)

Linia de sine este impartita in trei portiuni, cu o impartire diferita a curentilor in sine. Orientarile pozitive ale curentilor si tensiunilor si inceputul calculelor pentru fiecare din sectiuni sunt aratate in desene.

In cazul determinarii modificarii curentilor si tensiunilor de-a lungul fiecarei sectiuni este necesar sa se tina seama de curentii care ajung in sine din sectiunile  invecinate. Aceasta imprejurare complica mult tabloul general de distributie a curentilor si tensiunilor de-a lungul liniei asimetrice fara joante izolante. Rezolvarea exacta a ecuatiilor pentru curenti si tensiuni de-a lungul liniei asimetrice este dificila, intrucat constantele integrarii pentru toate cele trei sectiuni sunt legate reciproc.

In scopul simplificarii ecuatiilor privind coeficientii cuadripolului asimetric de linie, s-au luat doua variante admise in schema de substitutie. In prima varianta fiecare linie de sine longitudinal vecina este inlocuita cu trei impedante echivalente, concentrate pentru capat Z,Z,Z si pentru inceput Z, Z, Z.

Schemele de substitutie ale liniei conform primei variante admise, in cazul unor sine de linie bune, sunt aratate in figur nr.III..5, iar pentru linia cu o sina intrerupta in fig. III..6

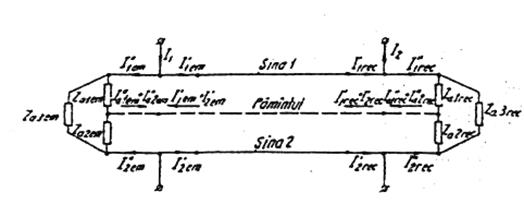
Fig. III. 6 - Schema de substituire ( sinele sunt bune)

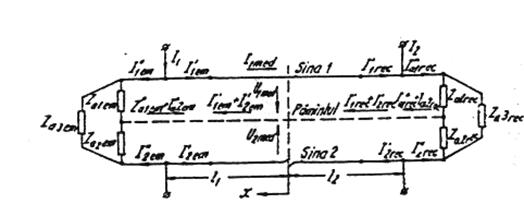
Fig. III. 7 - Schema de substituire ( sina  intrerupta)

In cazul variantei a doua admise, fiecare linie de sine longitudinal vecina este inlocuita cu doua impedante echivalente concentrate pentru capatul Z,Zsi inceputul Z, Z.

Schemele echivalente in cazul ambelor sine de linie bune sunt prezentate in figura nr. III.7, iar in cazul unui fir de sina intrerupt sunt aratate in fig nr. III..8.

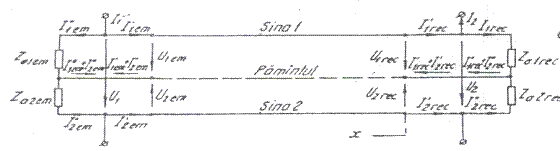
Ffig. III. 8 - Schema de substituire ( sinele sunt bune)

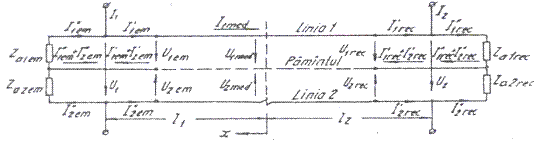
Fig. III. 9 Schema de substituire ( sina intrerupta)

In ambele variante admise la ridicarea ecuatiilor de calcul pentru impedantele echivalente concentrate, fiecare din liniile longitudinal vecine se examineaza separat de restul partilor schemei echivalente.

Pentru deductia unor ecuatii exacte si aproximative ale coeficientilor cuadripolului de sine ale liniei nelimitate se folosesc ecuatiile cunoscute, care exprima legile de modificare a curentilor si tensiunilor de-a lungul liniei.

U=Achx+Ashx+Achx+Ashx;

U=M+N;

I =y+y;

I = y+y.

In aceste ecuatii constantele integrarii se determina corespunzator cu conditiile limita pentru circuitele de cale nelimitate. Metoda deductiei ecuatiilor coeficientilor cuadripolului de sina pentru circuitele de cale nelimitate este identica cu metoda utilizata in cazul circuitelor de cale limitate . Deosebirea consta doar in alegerea conditiilor limita si a sistemului de ecuatii pentru determinarea constantelor de integrare.

In cazul analizei schemei echivalente a liniei asimetrice in intregime, compusa din trei sectiuni sunt 12 constante de integrare iar in cazul jumatatii de schema sunt 8 constante de integrare, pe cand in cazul analizei schemei de substitutie a circuitelor de cale nelimitate au fost patru constante de integrare. Din ecuatiile limita trebuie alcatuite atatea ecuatii cate constante de integrare sunt.

La analiza schemei de substitutie in ansamblu in cazul unor fire de sine bune pentru conditiile limita s-au obtinut 12 ecuatii cu 12 necunoscute.

-; -; -

=2I;

;

;

;

MNMN;

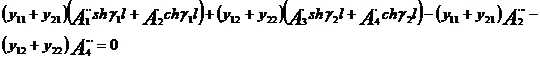
M

In cazul analizei jumatatii schemei de substituie, cand este rupt un fir de sina, pentru conditiile limita s-au obtinut opt ecuatii cu opt necunoscute

La deductia ecuatiilor aproximative a coeficientilor cuadripolului de sine conform schemelor in figurilor prezentate, vor fi patru constante de integrare, ca si in cazul deductiei ecuatiilor pentru circuitele de cale limitate, fapt pentru care nu se indica sistemele de ecuatii. Pentru circuitul de cale simetric constantele de integrare se gasesc conform urmatoarele opt ecuatii obtinute din conditiile limita:

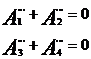
Coeficientii cuadripolului de sine in cazul lui ; ; si a schimbarii de la :

in cazul lui iar in cazul schimbarii de la 0 la ∞;

Pentru calculele practice este comod sa se exprime coeficientul cuadripolului de cale prin functiile circuitului de cale:

unde

In cazul valorii adica in cazul ruperii firului de sina la mijlocul caii la mijlocul caii de sine, ecuatiile functiilor se simplifica.

In circuitele de cale cu prelucrarea curentului conform schemei de substitutie, releul de cale se atrage datorita fortei electromotoare care se induce in bobinele de cale de catre curentul din sine.