Legea transformarii de energie in conductori

Legea transformarii de energie in conductori

Experienta arata ca orice corp conductor aflat in stare electrocinetica degaja caldura in mediul inconjurator, fenomen care inceteaza atunci cand starea electrocinetica dispare. Caldura degajata se produce in toata masa corpului, in orice punct al acestuia, si fiind legata de existenta procesului de conductie electrica (ca efect al electrocineticii, care este un fenomen strict electromagnetic) se considera ca ea provine din energia campului electromagnetic, ce poate fi numita energie electromagnetica. Prin urmare, exista urmatorul fenomen, ca aspect calitativ: in procesul conductiei electrice are loc o transformare a energiei electromagnetice in caldura (energie termica) si uneori -in cazul electrolitilor- si in transformari de substanta, deci in energie chimica (v. § 1.3.12), sediul acestei transformari fiind corpul conductor.

Legea transformarii de energie in conductori determina cantitativ fenomenul natural al degajarii de caldura in corpurile conductoare aflate in stare electrocinetica prin modele care implica marimile de stare ale electrocineticii ( i si , ca marimi fizice ce cuantifica procesul conductei) si de stare electrica (prin marimile u si ), precum si marimile de proces: energie (W), putere (P) si densitate de volum a puterii (p).

Cronologic, in activitatea de cunoastere si cercetare a campului electromagnetic, legea aceasta a fost formulata la nivel global de catre fizicianul englez James P. Joule pentru cazul particular al unui conductor electric, stabilindu-se apoi si o forma generala locala.

Legea lui Joule

Daca un corp conductor, avand rezistenta R, se afla in stare de conductie electrica exprimata cantitativ de intensitatea curentului de conductie i, se constata ca intr-un interval de timp (de la momentul t₁ la momentul t₂) conductorul va degaja ireversibil, in mediul inconjurator, energia W care -exprimata in unitatea de masura SI a energiei juole (J) sau watt secunda (Ws)- se determina cu expresia:

(1.99)

care este o forma globala primitiva a legii transmiterii de energie in conductori.

Exprimata in calorii, energia degajata (caldura Q) se determina cu:

(1.99')

In ambele relatii, (1.99 si (1.99'), R se exprima in ohmi, i in amperi si t in secunde.

Forma integrala a legii transformarii de energie in conductori

Din expresia legii (1.96) a conductiei electrice se poate explicita termenul R, obtinandu-se: R= (u_f + e)/i , care introdusa in locul lui R din legea (1.99) conduce la:

(1.100)

care este o noua forma integrala (globala, relativa la un conductor filiform) a legii transformarii de energie in conductori. Operatorul integrala se poate distribui (fiind liniar) intre cei doi termeni, obtinandu-se o noua forma a acestei legi:

(1.100')

ea are doi termeni:

W_R, corespunzator integrarii in intervalul de timp (t₂ - t₁) a produsului dintre tensiunea electrica in lungul firului u_f (determinata de campul coulombian existent in conductor de-a lungul axului sau) si intensitatea curentului electric de conductie i;

W_is, corespunzator integrarii in intervalul de timp (t₂ - t₁) a produsului dintre t.e.m e (determinate de campurile: imprimat  si solenoidal existente in conductor de-a lungul axului sau) si intensitatea curentului electric de conductie i.

Termenul W_R reprezinta energia disipata in conductor datorita campului coulombian, iar termenul W_is reprezinta energia datorita campurilor imprimat si/sau solenoidal, ambele de provenienta "exterioara" conductorului si specifice asa-numitelor "surse electrice" (v. cap.4 si cap.8). Prezenta, in acest proces de disipare termica, a campurilor coulombian si solenoidal arata ca energia termica degajata de conductor este de origine electromagnetica.

In cazul particular in care = 0 (ceea ce inseamna ca nu exista o variatie in timp a campului magnetic iar conductorul este imobil) si = 0 (adica nu exista neomogenitati de material in cadrul conductorului si nici neuniformitati de acceleratie etc.) expresia (1.100) devine:

(1.101)

din care se poate deduce si puterea disipata de conductor:

(1.102)

care este o alta forma globala (integrala) a legii transformarii de energie in conductori potrivit careia intr-un conductor filiform puterea totala dezvoltata este egala cu produsul intre tensiunea de-a lungul axei conductorului si intensitatea curentului conductorului.

Deoarece aceasta transformare de energie are loc in procesul de conductie electrica, se poate apela din nou la legea conductiei electrice sub forma (1.96) din care il explicitam pe u_f :

u_f = Ri - e,

care introdusa in forma (1.102) a legii transformarii de energie in conductori da:

(1.102') P = (Ri - e)i = Ri² - ei =P_R -P_is,

care este o alta forma integrala a legii ce evidentiaza, prin cei doi termeni ai sai, ca:

o parte din puterea P transformata in procesul conductiei electrice, termenul P_R = Ri², singurul diferit de zero (si imtotdeauna pozitiv) in conductoarele fara camp imprimat (E_i = 0) si fara camp de inductie (E_s = 0), este puterea disipata, adica puterea dezvoltata ireversibil sub forma de caldura in conductori (legea lui Joule);

- cealalta parte a puterii P transformata in procesul conductiei electrice, termenul P_is = ei reprezinta puterea generata (ceea ce explica semantic denumirea data lui e, de tensiune electromotoare) de eventualele surse electrice existente in lungul conductorului si evidentiate de marimile  si . Acest termen poate fi pozitiv sau negativ; cand ei > 0 sursa produce energie, iar cand ei < 0 sursa absoarbe energie (de exemplu, cazul unui acumulator electric "pus la incarcat" - v.cap.4).

Modelul local al transformarii de energie in conductori

Prin forma locala se exprima logic, transformarea de energie localizata in fiecare punct al conductorului, in functie de  situatia locala a campului electric caracterizat de si a celui electrocinetic caracterizat de , pe de o parte si densitatea de volum a puterii transformate in acel punct, care se noteaza cu p si se exprima in wati pe metru la cub (W/m³), pe de alta parte.

Daca s-ar cunoaste distributia acestei densitati de volum a puterii transformate, adica p(P) in PIW_f, unde W_f este domeniul ocupat de firul conductor, cu un volum v_c, atunci puterea P transformata in intregul domeniu W_f al conductorului, va fi:

(P) ,

in care volumul elementar dv fiind unul oarecare din firul conductor W_f , poate fi ales preferential sub forma unui cilindru elementar cu sectiunea de arie A si cu lungimea elementara dl plasat pe directia axei G_c a conductorului filiform si orientat astfel ca avand versorul perpendicular pe sectiunea de arie A si cu lungimea dlIG_c cu avand versorul t tangent la G_c , in acelasi sens cu, asa cum se arata in figura 1.25, astfel ca , adica sunt omoparalele.

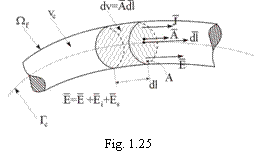In aceste conditii, redate in figura 1.25, relatia (P) se poate scrie sub forma:

   (P')

si daca il inlocuim pe P cu expresia lui din legea (1.102'), in conditiile din figura 1.25 se va obtine:

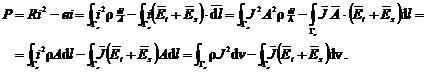(P")

In expresiile (P') si (P'') s-a tinut cont de omoparalelismul vectorilor , existente in conditiile unui conductor filiform omogen, precum si de faptul ca pentru o sectiune prin conductorul filiform cu aria foarte mica (daca). Egalandu-se intre ele expresiile din membrul drept al ultimelor egalitati (P') si (P'') rezulta:

(1.102")

si, deoarece dv este un element de volum oarecare rezulta in definitiv:

; (1.103)

care este modelul local al legii transformarii de energie in conductori. Primul termen poate fi scris si in forma , deoarece -conform legii (1.95') - astfel ca legea (1.103) se poate descrie astfel:

. (1.103')

Primul termen din aceste expresii ale lui p reprezinta densitatea de volum a puterii disipate ireversibil sub forma calorica (fiind in orice situatie pozitiv), iar al doilea , este densitatea de volum a puterii transformate (primita sau cedata de conductor) in punctele in care exista camp imprimat si/sau solenoidal (deci este densitatea de volum a puterii generate in conductori, cu semnul + T produsa si cu T absorbita).

In cazul in care intr-un punct din conductor nu exista camp imprimat si camp solenoidal, legea transformarii de energie in conductori, sub forma locala, este:

. (1.103")