Ecuatiile lui Maxwell

Ecuatiile lui Maxwell

Formele locale, de punct, ale legilor generale de structura si evolutie a campului electromagnetic -adica ale legilor: circuitului magnetic (1.88), inductiei electromagnetice (1.82), fluxului electric (1.66') si fluxului magnetic (1.69')- constituind un sistem de ecuatii cu derivate partiale, poarta denumirea generica de ecuatiile lui Maxwell.

Aceste ecuatii, exprimate in functie de punct si de timp, completate -in concordanta cu particularitatile sistemului fizic de tip electromagnetic analizat- si cu alte ecuatii in forma locala ale legilor campului electromagnetic, precum si cu conditiile la limita si initiale, asigura rezolvarea -in conditii de unicitate (v. § 1.5.1)- a oricarei probleme de camp electromagnetic, deoarece ecuatiile lui Maxwell reprezinta, datorita formei lor locale, modelele cele mai adecvate pentru determinarea -corespunzator conceptiei sistemice de localizare a tuturor actiunilor si proprietatilor fizice- a oricarui sistem electromagnetic.

Exista mai multe modele ale ecuatiilor lui Maxwell, in functie de momentul istoric al formularii lor, de conditiile impuse sistemului fizic electromagnetic, de teoria adoptata pentru studiul campului electromagnetic, de sistemul de coordonate adoptat, de procedura de rezolvare matematica si informatica aleasa si de multe altele. In cadrul acestui subcapitol, ne vom limita la prezentarea acelor forme ale ecuatiilor lui Maxwell care sunt folosite in teoria macroscopica clasica a campului electromagnetic si care permit solutionarea problemelor de camp electromagnetic prin tehnici informatice (v. subcapitolele 9.2 si 9.3).

1. Ecuatiile de baza ale lui Maxwell

Sub forma lor initiala, asa cum au fost elaborate de insusi Maxwell, ecuatiile lui Maxwell se refera la electrodinamica macroscopica a mediilor continue, netede (in care functiile sunt continue si derivabile) si imobile, adica in cazul unor medii in repaus (cu viteza ), liniare, omogene si izotrope, fara polarizatie electrica permanenta (), fara magnetizatie permanenta () si fara camp imprimat (); ele se prezinta astfel:

, (1.105M1)

, (1.105M2)

, (1.105M3)

, (1.105M4)

in care: si sunt vectorii intensitatii locale a campului electric si inductiei electrice locale; _{si sunt vectorii intensitatii locale a campului magnetic si inductiei magnetice locale; este vectorul densitatii curentului electric de conductie si qv este densitatea de volum a sarcinii electrice, ultimele doua marimi fiind si ele functii de punct (locale). Toate aceste marimi pot fi (sunt) si functii de timp.}

_{Prima ecuatie -ecuatia intai a lui Maxwell (1.105M1)- reprezinta forma locala -in conditiile precizate anterior- a legii circuitului magnetic (1.83IV ) in care termenii si , pentru ca} ; ea se mai numeste si ecuatia lui Maxwell-Ampere. A doua ecuatie (1.105M2) -denumita ecuatia a doua a lui Maxwell sau, inca, ecuatia lui Maxwell-Faraday- reprezinta forma locala a legii inductiei electromagnetice (1.81^III) in care termenul _{deoarece s-a considerat initial} . A treia ecuatie (1.105M3) este forma locala a legii fluxului electric (1.65), iar ecuatia a patra (1.105M4) reprezinta forma locala a legii fluxului magnetic (1.67).

2. Ecuatiile generale ale lui Maxwell

Pentru determinarea campului electromagnetic, adica a celor patru marimi de stare ,, _{si ale acestuia, cele patru ecuatii ale lui Maxwell (1.105) se completeaza cu legile de material sub formele:(1.77) - a polarizatiei electrice temporare, (1.80) - a magnetizatiei temporare si (1.95) - a conductiei electrice, care sunt modele locale (de punct), valabile numai pentru materialele uniforme, liniare si avand} , _si .

Astfel, la cele patru ecuatii (1.105) din § 1 se mai adauga ecuatiile:

(1.106 M5)                    ,

(1.106 M6)                    ,

(1.106 M7)                    ,

in care ε, μ si γ sunt marimile de material: permitivitatea absoluta, permeabilitatea absoluta si conductivitatea electrica, toate indicate pentru materiale liniare, omogene si izotrope.

Sistemul celor patru ecuatii de baza ale lui Maxwell (1.105), in care si _{se inlocuiesc cu expresiile lor din (1.106M5) si (1.106M6), iar operatorii liniari -scrisi in coordonate carteziene, ca si vectorii de stare} si se dezvolta prin:

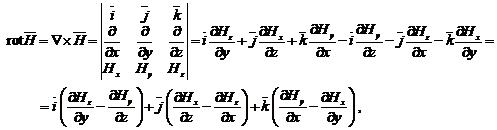
cu:

cu:

si:

in care sunt versorii celor trei axe ale sistemului de coordonate cartezian, iar E_x , H_x si J_x , E_y , H_y si J_y , E_z , H_z si J_z sunt componentele dupa directiile , ale vectorilor si respectiv.

Inlocuind aceste dezvoltari in ecuatiile (1.105) si identificand, membru cu membru, componentele de pe aceleasi axe ale sistemului cartezian , ecuatiile de baza ale lui Maxwell formeaza urmatorul model de opt ecuatii scalare simultane cu derivate partiale cu sase functii necunoscute :

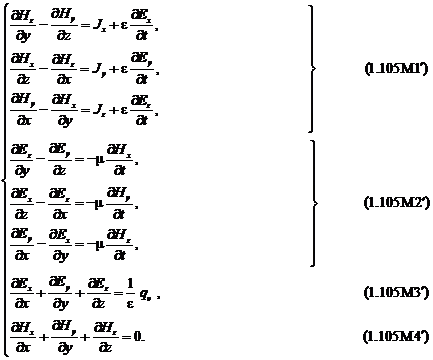
Conform teoremei de unicitate a campului electromagnetic pentru medii liniare si uniforme (v. § 1.5.1) si teoriei sistemelor de ecuatii cu derivate partiale (din Matematica), sistemul de ecuatii (1.105M1').(1.105M4') precedent are o solutie unica ( si ) intr-un domeniu dat (pentru care se cunosc ε, μ, γ si ), daca se dau: sursele q_v si J_x , J_y , J_z , conditiile la limita pe frontiera domeniului in care se determina campul electromagnetic (prin componentele tangentiale E_t sau H_t ) si conditiile initiale.

3. Modele ale ecuatiilor lui Maxwell

Intr-un caz mai general, ecuatiilor lui Maxwell (1.105) si ecuatiilor (1.106) li se mai ataseaza si forma locala (1.92) a legii conservarii sarcinii electrice (1.90), adica:

, (1.107)

in conditiile in care mediul este imobil (), ceea ce se scrie si prin:

(1.107')

In ecuatiile lui Maxwell (1.105), precum si in ecuatiile (1.106) si (1.107), atat marimile de stare macroscopica a campului electromagnetic (nestationar) si a corpurilor, cat si coordonatele spatiale si variabila temporara t, sunt raportate la un sistem de referinta inertial fix, care -in cazul considerat al unui mediu mobil- coincide cu referentialul propriu (adica sistemul de referinta inertial atasat fiecarui punct al mediului de camp aflat in repaus, local si instantaneu, in raport cu substanta din vecinatatea punctului respectiv - v. § 1.1.1).

In lucrarea: Mandru, Gh. , Radulescu, M.M. "Analiza numerica a campului electromagnetic", Editura Dacia, Cluj-Napoca, 1986 se prezinta un model pentru ecuatiile lui Maxwell, complectate cu ecuatiile (1.106) si (1.107') scris intr-un sistem general de coordonate curbilinii triortogonale, un model foarte indicat pentru calculele realizate cu sisteme informatice, pe care il reproducem in continuare.

Sistemul general de coordonte curbilinii triortogonale este caracterizat de:

- coordonatele (x₁, x₂, x₃) definite in functie de cele carteziene (x, y, z) prin relatiile:

, ,

sau invers:

, , ;

- coeficientii lui Lamé (v. Matematica) h₁, h₂, h₃ care sunt unitati locale de lungime, definiti prin expresia distantei elementare dl dintre doua puncte elementar vecine si si anume:

= dl cu .

In acest sistem general de coordonate curbilinii, ecuatiile lui Maxwell (1.105M1').(1.105M4') si ecuatia (1.107') se transcriu printr-un model constand din noua ecuatii diferentiale scalare, cu derivate partiale de ordinul intai in raport cu timpul si cu coordonatele spatiale si anume:

(1.105M1'')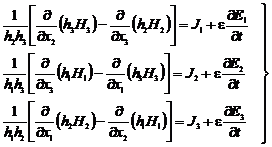       

(1.105M2'')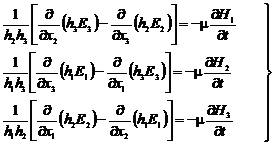      

(1.105M3'')              

(1.105M4'')         

(1.107'')            

Expresiile coordonatelor si parametrilor Lamé si formulele de transformare pentru sistemele uzuale de coordonate curbilinii triortonormale sunt:

- sistemul de coordonate carteziene:

- sistemul de coordonate cilindrice circulare:

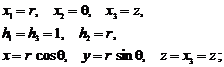
- sistemul de coordonate sferice:

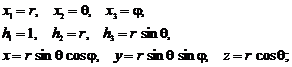
- sistemul de coordonate eliptice (ale cilindrului eliptic):

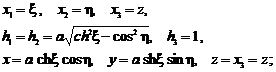
- sistemul de coordonate parabolice (ale cilindrului parabolic):

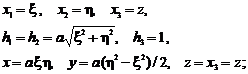
- sistemul de coordonate ale elipsoidului alungit:

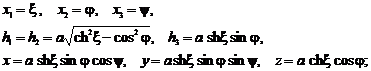
- sistemul de coordonate ale elipsoidului aplatisat:

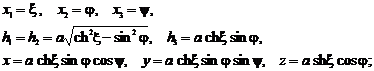
- sistemul de coordonate paraboloidale:

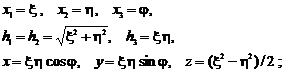
- sistemul de coordonte toroidal:

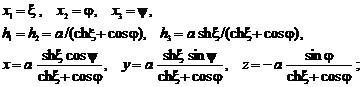
- sistemul de coordonate biaxiale:

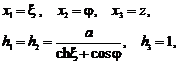
In relatiile de mai sus a este un numar real reprezentand semiaxe ale suprafetelor de revolutie, raze focale sau raza torului.

Modelul general (1.105M1''), (1.105M2''), (1.105M3''), (1.105M4'') si (1.107''), al ecuatiilor lui Maxwell, permite adaptarea lui la orice caz concret-practic, cu alegerea sistemului de coordonate cel mai potrivit topologiei mediului (corpului) la care se refera aplicatia si cu scrierea imediata a unor modele numerice pentru problemele de camp electromagnetic, rezolvabile prin tehnicile informatice ale diferentelor finite si variationale prin metoda elementului finit (v. subcapitolele 9.2 si 9.3).

4. Ecuatiile lui Maxwell - Hertz

Ecuatiile lui Maxwell (1.105M1).(1.105M4) au fost generalizate de Hertz, prin includerea  cazului general in care mediul (corpurile din camp) sunt in miscare, cu o viteza locala , rezultand modelul:

(1.108)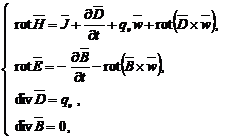                         

cunoscut sub numele de ecuatiile lui Maxwell-Hertz.

Modelul (1.108) se obtine din formele integrale ale legilor (circuitului magnetic si inductiei electromagnetice), presupunand -in acord cu ipoteza domeniului total antrenat- ca liniile inchise in lungul carora se calculeaza circulatia campurilor si suprafetelor deschise care se sprijina pe aceste contururi si prin care se calculeaza fluxurile campurilor sunt antrenate de corpuri cu viteza locala .

In ecuatiile Maxwell-Hertz (1.108) apar urmatorii termeni suplimentari fata de ecuatiile de baza ale lui Maxwell (1.105):

- termenul care exprima densitatea (de suprafata) a curentului electric de convectie, termen confirmat de experienta;

- termenul ce reprezinta densitatea (de suprafata) a curentului Roentgen teoretic, termen infirmat partial de experienta - care confirma insa expresia - v. § 1.3.8 / relatia _{(1.83IV );}

_{- termenul - ce corespunde inductiei electromagnetice prin miscare, fiind verificat intotdeauna de experienta.}

_{Spre deosebire de ecuatiile lui Maxwell, care -asa cum s-a vazut- nu sunt invariabile la schimbarea sistemelor de referinta inertiale, daca se foloseste (presupunandu-se valabila) transformarea Galilei (v. Mecanica solidelor), ecuatiile lui Maxwell-Hertz sunt invariante la aceasta transformare, marimile} , , si fiind definite in mod absolut. Deoarece experienta infirma atat ecuatiile lui Maxwell-Hertz cat si transformarea Galilei, rezulta ca aceste ecuatii au fost obtinute printr-o generalizare doar teoretica, aproximativ corecta. Deoarece termenii din aceste ecuatii infirmati de experienta, fiind vorba de , au o contributie neglijabila la determinarea (calculul) campului electromagnetic in raport cu ceilalti termeni corecti, aceste ecuatii se utilizeaza in tehnica fiind deosebit de comode in aplicatii si furnizand solutii care aproximeaza destul de exact solutiile corecte care s-ar obtine pe baza electrodinamicii relativiste. In acest scop, al aplicatiilor corecte din tehnica, ecuatiile Maxwell-Hertz se completeaza cu relatiile de legatura si cu cele de material (1.106) si (1.107), ca si in cazul ecuatiilor lui Maxwell.

5. Relatia lui Maxwell

Aceasta relatie este un model care stabileste legatura intre constantele universale ale electromagnetismului ( si - v. § 1.2.3) si viteza de propagare a luminii in vid , avand forma cunoscuta (1.54), adica:

,

in care este permitivitatea vidului, iar - permeabilitatea vidului. In forma aceasta, relatia este scrisa in sistemele de unitati CGSem, MKSA (v. Fizica) si in SI, in care constanta lui Gauss se ia egala cu unitatea. Intr-o forma mai generala (care inglobeaza si sistemul simetric de unitati de masura a lui Gauss), relatia lui Maxwell se scrie:

. (1.109)

Constanta lui Gauss g₀ este o constanta universala, care in toate sistemele uzuale de unitati de masura este g₀ = 1, in afara de sistemul CGS Gauss in care g₀ = 1/c₀ (adica inversul vitezei de propagare a luminii in vid).

Membrul drept al relatiei lui Maxwell (1.109) este egal cu viteza de faza a undelor electromagnetice in spatiul vid, nelimitat, asa cum rezulta din ecuatiile lui Maxwell (v.§ 7.4.4). Relatia lui Maxwell, care exprima identitatea dintre aceasta viteza si viteza de propagare a luminii in vid, poate fi considerata fie ca o lege experimentala (a carei verificare a sugerat lui Maxwell natura electromagnetica a luminii), fie ca o conditie de invarianta a ecuatiilor lui Maxwell la schimbarea sistemului inertial de referinta cu transformarea Lorentz (in Fizica relativista). Totusi, ultima interpretare arata ca aceasta relatie a lui Maxwell reflecta proprietatile fizice de structura, mult mai generale decat identitatea undelor luminoase cu a celor electromagnetice. Asupra acestei chestiuni se va reveni in capitolul 7, consacrat propagarii campului electromagnetic.