|
|
|
Legea conductiei electrice
Aceasta este o lege de material care exprima un fapt experimental evident si anume: conductia electrica dintr-un corp sau starea sa electrocinetica este determinata de campul electric in care se afla corpul si -in mod semnificativ- de natura materialului (substantei) corpului.
Constatarea aceasta experimentala reprezinta aspectul fenomenologic (calitativ) caruia legea conductiei electrice cauta sa-i postuleze un model care sa determine cantitativ dependenta dintre "nivelul" conductiei electrice, intensitatea campului electric si "contributia" de material a corpului, prin relatia vectoriala de punct si de timp:
.
Modelul aplicatiei vectoriale instantanee (de timp
t):
, in orice punct P
apartinand corpului 
, depinde puternic de natura materialului si de starea
lui. Astfel, pentru unele materiale (denumite, generic, izolanti) practic,
chiar la valori mari ale campului -care insa nu trebuie sa
depaseasca asa-numita "rigiditate dielectrica" 
ce reprezinta tot
o marime de material (ea va fi prezentata in capitolul 2)-
conductia electrica este practic inexistenta (deci 
); in schimb la alte materiale (denumite, generic,
conductori) densitatea de curent 
este practic direct
proportionala cu intensitatea campului electric 
.
Legea conductiei electrice poate fi exprimata
local (ca functie de punct) - cazul general si sub forma
integrala (globala) - relativ la o curba 
considerata in
mod particular printr-un conductor filiform.
In unele lucrari, legea conductiei este denumita legea lui Ohm.
Modelul local al legii conductiei electrice
In cazul unui domeniu 
format dintr-un conductor uniform (omogen si
izotrop) si liniar, legea
conductiei electrice se exprima prin modelul:
, (1.95)
unde 
este conductivitatea electrica, o
marime de material (care este specifica fiecarei substante)
ce a fost prezentata in paragraful 1.2.3 (v. tabelul 1.3).
Deoarece prin definitie 
, adica rezistivitatea electrica a materialului (v.
§ 1.2.3 si tabelul 1.3), modelul (1.95) se poate scrie si in forma:
(1.95') 
,
care reprezinta tot legea conductiei electrice locale in medii conductoare, uniforme si liniare.
Daca mediul
conductor nu este omogen si/sau are neuniformitati de
acceleratie si de temperatura, este iradiat etc., atunci in
punctele de neuniformitate (chiar daca materialul este liniar si
izotrop) se produce un camp electric imprimat (v. § 1.2.2 si subcap. 4.3),
cu intensitatea 
, astfel ca in aceste puncte campul electric are
intensitatea, conform expresiei (1.28E): 
, si legea conductiei electrice sub forma
locala devine:
(1.95") 
,
in care 
- conductivitatea
electrica si - intensitatea
campului electric imprimat (ambele marimi de material) iar 
este intensitatea
campului electric coulombian (v. § 1.2.2. si subcap. 2.2).
In cazul in care domeniul
conductor neomogen, insa izotrop si liniar, se afla intr-un
camp electromagnetic variabil in timp (cu 
) sau/si se deplaseaza in camp cu o viteza
locala 
- astfel ca rot
, atunci -conform legii inductiei electromagnetice
(1.82)- in conductor exista si un camp magnetic solenoidal (cu
intensitatea 
), ceea ce face ca intr-un punct 
campul electric
sa aiba intensitatea - conform relatiei (1.28 E): 
si legea
conductiei electrice (1.95) capata forma:
(1.95"') 
sau:
(
) 
.
In cazul unor conductoare
anizotrope (dar liniare), marimea de material din legea (1.95) se
inlocuieste cu tensorul
conductivitatii electrice 
care se
exprima printr-o matrice cu 9 (eventual 3) valori scalare specifice
materialului (v. § 4.6.2).
Modelul global (integral) al legii conductiei electrice
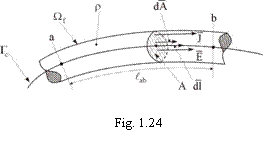Considerandu-se cazul particular al unui domeniu conductor 
filiform, foarte lung in raport cu cea mai mare dimensiune a
sectiunii transversale (fig. 1.24), adica avand 
, in asa fel ca in orice punct P al sectiunilor transversale de arie A de-a lungul firului conductor vectorii de punct 
si 
si vectorul
elementului de curba orientat 
, al axei 
a firului conductor,
precum si elementul de arie transversala orientat 
(v. fig. 1.24), sunt
omoparalele, ceea ce inseamna:
(HP) 
si efectuandu-se, in fiecare memmbru al egalitatii
(), integrala curbilinie dupa axa a firului conductor 
intre doua puncte
oarecare 
(v. fig. 1.24) se
obtine:
. (IC)
In conditiile (HP) de omoparalelism si
distribuind integrala (ca operator liniar) in membrul din stanga
egalitatii (IC) in conditiile unui conductor filiform realizat
dintr-un material uniform, deci cu 
, se obtine:
(RI)
in care:
- conform definitiei (1.43'), 
, adica tensiunea
electrica in lungul firului, intre punctele a si b (prin
conductor);
-conform definitiei (1.49), 
, adica tensiunea
electromotoare pe portiunea 
a conductorului;
- valoarea absoluta a densitatii de
curent, J, in conditiile unui
conductor filiform, cu sectiunea transversala pe curba cu aria foarte
mica A (v. fig. 1.24), se poate
considera constanta, adica in 
, unde i este
intensitatea curentului electric de conductie ce descrie starea
electrocinetica a conductorului filiform. In aceste conditii, 
, deoarece 
, adica lungimea firului conductor intre punctele a si b considerate.
Termenul 
este denumit rezistenta electrica a unui
conductor filiform, intre doua puncte ale sale a si b, intre care
conductorul este omogen (
), izotrop si cu aria sectiunii transversale
constanta (A=
.).
Scriind integrala din membrul drept al relatiei (IC) sub forma:
, (R')
unde:
(R)
este rezistenta electrica a conductorului filiform intre doua puncte ale sale, relatia intermediara (RI), tinand seama de cele de mai sus, devine:
(1.96')
sau:
(1.96'')
si (mai simplu) :
, (1.96)
care constituie modelul integral (global, relativ la un conductor filiform din material liniar) al legii conductiei electrice, care dimensional reprezinta, termen cu termen, tensiuni electrice.
Deoarece, prin definitie 
, denumita conductanta conductorului filiform,
legea (1.96) poate fi transcrisa si in forma:
(1.96''') 
,
care este dimensional o relatie intre curenti electrici.
Daca un conductor filiform este omogen, izotrop si cu sectiunea constanta, rezistenta lui electrica se determina cu relatia:
(1.97) 
,
unde l este
lungimea conductorului filiform si se exprima, in sistemul
international, SI, prin unitatea de masura denumita ohm, cu simbolul 
. Asa se explica faptul ca rezistivitatea are
unitatea de masura SI ohm metru (
) asa cum s-a aratat in paragraful 1.2.3. In
aplicatiile tehnice ale retelelor electrice, la care conexiunile se
fac din conductoare filiforme, tabelele cu rezistivitatea unor materiale
electrice il exprima pe 
in 
, care rezulta din (1.97) prin faptul ca 
(ca
rezistenta electrica specifica, pentru 1mm2 de
sectiune si o lungime de 1m), deoarece la conductoarele filiforme
este mai simplu ca aria sectiunii lor sa se exprime in mm2
(si nu in m2!) iar lungimea in metrii. Ca exemplu, cuprul are
rezistivitatea 
.
Acelasi conductor filiform, omogen, izotrop si
cu A=
(pe toata lungimea lui l considerata), are conductanta:
(1.97') 
,
unde 
este conductivitatea
materialului (v. § 1.2.3). Conductanta G
in SI, are unitatea de masura unu pe ohm (
), denumita siemens
(cu simbolul S).
Dimensional, din legea (1.96) rezulta:
(1.98) 
sau 
.
Din felul de exprimare (1.96') sau (1.96'') a legii
conductiei electrice rezulta ca s-a ales acelasi sens de
integrare in lungul curbei (v. fig. 1.24), atat
pentru 
si e
cat si pentru i (prin 
), adica 
, sau 
(deci 
) ceea ce inseamna ca sensul de referinta
al versorului normalei 
la sectiunea
transversala prin conducor a fost ales acelasi cu sensul de
referinta al versorului tangentei 
la curba (axul conductorului
filiform). Daca unul din sensurile de referinta, sau , se inverseaza, atunci in legea (1.96) 
si e sau, respectiv, i vor primi semnul minus. Asupra sensurilor de referinta
si asocierea lor, in cazul marimilor electrice de circuit: 
si i, se va reveni pe larg in subcapitolul
8.2.
In cazul unui conductor filiform din material liniar in
care nu exista campuri imprimate sau solenoidale (cu 
si 
=0), caz in care conductorul se numeste pasiv, legea
(1.96) ia forma:
(1.96
) 
sau 
,
forme frecvent denumite "legea lui Ohm".
