Deformatii si deplasari

Corpurile sub actiunea sarcinilor exterioare sufera si deformatii.

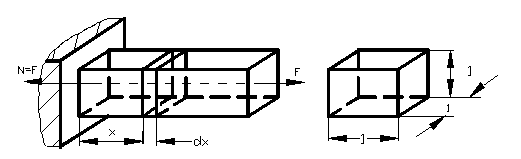
Figura 28

Daca avem o bara si din ea se decupeaza un cub cu latura egala cu

unitatea( 1mm, 1cm ) se constata in cazul unei solicitari , pe de o parte

modificarea lungimii muchiilor sale (se alungeste sau se scurteaza),

iar pe de alta parte , se modifica unghiurile initial drepte dintre doua

muchii (unghiurile devin ascutite sau obtuze).Modificarea lungimii

segmentelor drepte se numeste deformatie liniara ( sau lungire,

respectiv scurtare ), iar modificarea unghiurilor drepte deformatie

unghiulara.

1. Deformatii liniare

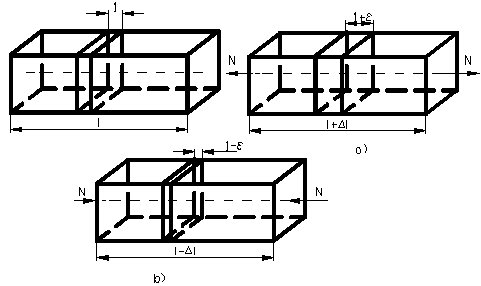
Figura 29

La solicitarea axiala avem doua cazuri : de intindere sau de compresiune , functie de sensul fortei  ( N ); Δl o sa fie pozitiv sau negativ.

Se considera o bara dreapta solicitata ca in figura urmatoare:

in cazul a) din figura 29, avem o alugire a barei cu Δl.

Daca inainte de deformare lungimea barei a fost (l) , iar dupa

Δl= l₁-l, reprezinta deformatia liniara sau lungirea totala a barei. In cazul b) din figura 29, bara este solicitata la compresiune de forta , iar deformatia barei se manifesta prin scurtarea totala Δl. Raportand deformatia liniara Δl= dl , a intregii bare la lungimea initiala l , se obtine deformatia specifica (lungirea sau scurtarea specifica) notata cu ε = Δl /l, notiune de baza in studiul deformatiilor corpurilor asupra sarcinilor . [ε]=si deci [ε]= este adimensionala si poate fi pozitiva sau negativa dupa cum

reprezinta o lungire in cazul barei solicitata la intindere, sau o

scurtare la bara comprimata ( figura 30).

Deformatia specifica provine din faptul ca reprezinta deformatia

liniara a unui tronson din bara avand initial lungimea egala cu

unitatea,  astfel lungimea tronsonului devine dupa deformare 1+ε

respectiv 1-ε dupa cum bara s-a alungit sau s-a scurtat.

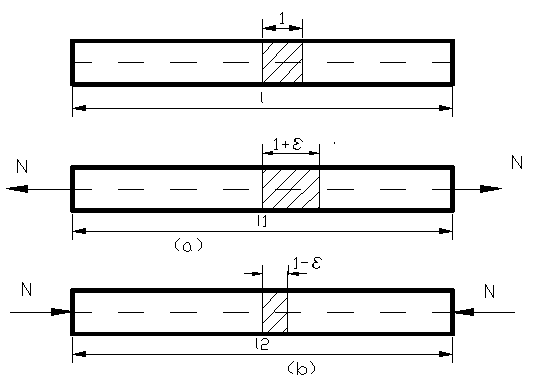
Figura 30

Exemplu:

Daca la o bara ε=0,004 , aceasta inseamna ca la fiecare tronson cu

lungimea de ( 1m ) din bara , s-a alungit cu 0,004m, adica cu 4mm , din relatia; dl=ε.l de unde se poate determina direct lungirea sau scurtarea totala a unei bare dl = Δl=ε.l daca se cunoaste ε .

2. Deformatii unghiulare

Pentru ilustrarea acestui tip de deformatii se considera o bara

solicitata ca in figura 31.

Prin deformarea barei , cele doua sectiuni 1-1si 2-2 luneca una fata de

alta, fara ca distanta initiala ( dx ) dintre ele sa se modifice.

In urma lunecarii celor doua sectiuni , fibrele longitudinale

se vor inclina cu un anumit unghi fata de directia lor initiala

aparand astfel , deformatia unghiulara γ.

Unghiul γ indica variatia unghiului drept, iar  tgγ = in cazul cand γ

este foarte mic (γ tinde la zero) , rezulta : tgγ γ si γ

, atunci cand unghiul tinde catre zero

(figura 32).

In jurul unui punct oarecare , alungirile sau scurtarile specifice ,pe directia axelor de coordonate , se noteaza cu : ε_xx, ε_yy, ε_zz , iar lunecarile specifice , in cele trei plane de coordonate , vor purta indicii planelor respective , adica : γ_xz, γ_xy, γ_yz.

Deformarea unui corp este determinata daca se cunosc elementele deformatiei ε si γ.

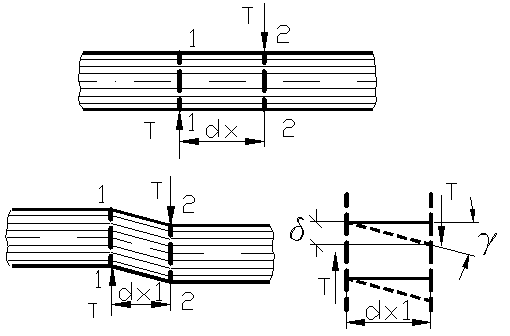
Figura 31

Figura 32