Stabilitatea unui SLCI

Stabilitatea unui SLCI

1. Stabilitate asimptotica (interna)

Fie raspunsul liber al SLCI reprezentat prin ecuatia (2.9) pentru o stare initiala x(t_o).

Definitia 2.1. : Spunem ca sistemul dinamic (2.9) este asimptotic stabil sau daca, indiferent de starea initiala x(t₀),

(2.21)

Remarca 2.3 : Notiunea de stabilitate asimptotica nu se refera la semnalul de intrare u(t) si, deci, la regimul fortat al sistemului.

Tinand cont de remarca 2.3, sistemul (2.9) este asimptotic stabil daca, oricare ar fi , avem:

.

Definitia 2.2 : Spunem ca sistemul dinamic (2.9) este instabil, daca:

Daca, pentru , solutia nu tinde spre zero dar nici spre infinit, vorbim despre stabilitate critica. Oscilatoarele armonice constituie un exemplu de astfel de sisteme.

Intr-adevar, daca m_i este ordinul de multiplicitate al radacinii:

;

putem scrie raspunsul tranzitoriu sub forma:

,

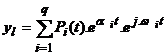cu polinom in t si de grad m_i-1 si

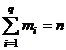(q fiind numarul de radacini distincte)

Tinand cont de aceasta relatie, avem:

()

Stabilitatea critica corespunde perechilor de radacini imaginare conjugate (cu partea reala nula), celelalte avand partea reala negativa.

Pentru studia stabilitatea unui SLCI trebuie deci sa rezolvam ecuatia sa caracteristica si sa studiem partea reala a radacinilor sale.

2 Stabilitatea intrare marginita-iesire marginita

Mai ales in abordare functionala, acest concept de stabilitate intrare marginita-iesire marginita (IMEM) este fundamental pentru analiza SCL.

Definitie2.3: Un SCL este stabil IMEM daca, aplicandu-i la intrare un semnal , rezulta la iesire un semnal

In definitia de mai sus, se poate utiliza p-norma i.e.

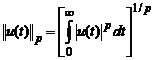, p=1, 2, .

Daca p= se obtine -norma, pe care o vom utiliza in continuare:

Am vazut ca:

y(t)=y_f(t)+y_l(t)=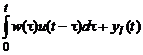

sau

Calculam p-norma lui y(t):

Impunem conditia de stabilitate IMEM:

Aceasta relatie este satisfacuta daca:

este finita (2.22)

este finita (2.23)

Conditiile (2.22) si (2.23) sunt intotdeauna satisfacute daca:

(1)                     

(2)                     

i.e. yl(t) si w(t) trebuie sa fie semnale de energie finita. Prima conditie este echivalenta cu stabilitatea asimptotica. Pentru cea de-a doua conditie avem cazurile ilustrate in figura de mai jos:

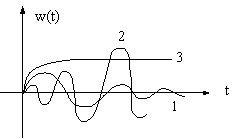
Functia pondere din cazul 1 corespunde unui sistem stabil IMEM, cel din cazul 2 unui sistem instabil, iar cel din cazul 3 unui sistem la limita de stabilitate.

Am vazut ca prima conditie de stabilitate IMEM este identica cu cea de stabilitate interna. Daca

; s_iIR si

, ,

sunt radacinile ecuatiei caracteristice, s-a aratat ca prima conditie este satisfacuta daca

     (2.24)

Ne ocupam de conditia (2):

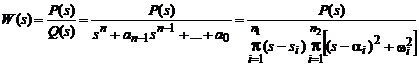
Dezvoltand in fractii simple, obtinem:

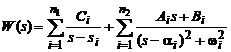
De aici, rezulta:

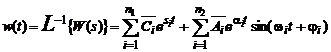
Constatam ca, pentru a satisface relatia (2), este necesara satisfacerea conditiei (2.24).

In concluzie, ambele conditii sunt satisfacute daca este indeplinit criteriul fundamental de stabilitate, adica radacinile polinomului caracteristic se gasesc in semiplanul complex C

Daca una sau mai multe radacini se gasesc pe axa imaginara, sistemul este instabil, dar la limita de stabilitate.

2 Criteriul de stabilitate Routh

Aplicarea conditiilor necesare si suficiente precedente necesita calculul radacinilor ecuatiei caracteristice a ecuatiei (2.9):

.

Este suficient sa determinam semnul partii reale a radacinilor; acest lucru poate fi efectuat cu ajutorul unor criterii care nu necesita decat calcule simple. Unul din acestea este criteriul Routh, a carui aplicare necesita construirea unei matrici de (n+1) linii, dupa cum urmeaza:

Primele doua linii a matricii lui Routh contin coeficientii ecuatiei caracteristice, iar celelalte linii contin elemente calculate in modul urmator:

;;

; ;

si asa pana la ultimul element.

Pe fiecare linie a matricii putem multiplica toate elementele cu un numar pozitiv oarecare. Atunci cand tabloul s-a terminat, examinam elementele din prima coloana pentru a aplica criteriul de stabilitate a lui Routh:

Numarul de schimbari de semn de pe prima coloana este egal cu numarul de radacini cu partea reala pozitiva ale ecuatiei caracteristice

Daca toate elementele de pe o linie sunt nule, ecuatia caracteristica are radacini cu partea reala nula.

Daca, de exemplu, aplicam criteriul lui Routh pentru a studia stabilitatea unui sistem de ordinul patru, obtinem urmatoarea matrice:

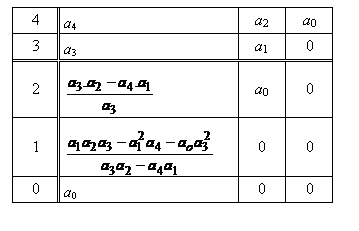
Presupunand ca toti coeficientii sunt pozitivi, conditiile de stabilitate impuse prin criteriul Routh sunt urmatoarele:

(2.25)

(2.26)

Conditia (2.26) se mai poate scrie:

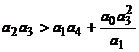, (2.24)

conditie care este mai stricta ca (2.22) si se foloseste singura, asa cum conditia necesara si suficienta pentru stabilitatea asimptotica este urmatoarea:

.