ISP

Flexibilitatea este capacitatea sistemului de productie de a se adapta rapid si economic la variatiile sarcinii de productie.

Proiectarea sistemului flexibil de fabricatie (SFF) trebuie sa fie intotdeauna precedata de analiza sarcinii de productie.

Analiza sarcinii de productie se compune din 2 faze:

Concetrarea tipologica, presupune selectarea din multimea tuturor reperelor prevazute a se realiza in SFF a catorva repere prezentative pentru intreaga sarcina de productie si care vor alcatui nucleul tipologic.

Detenta tipologica, urmareste acoperirea SFF cu un volum cat mai mare de lucrari.

Proiectarea unui SFF va porni intotdeauna de la reperele reprezentative urmand ca o data ce sistemul este constituit si functioneaza sa fie introduse in fabricatie in etapa de detenta tipologica si celelalte repere ramase.

Pentru ca un reper sa fie reprezentativ, acesta trebuie sa posede simultan atribute de stabilitate (adica acel reper sa apara in mod frecvent in fabricatie, ex. seria anuala de fabricatie) si consistenta (timpul unitar de prelucrare sa fie semnificativ mare in raport cu fondul anual de prelucrare al sistemului, ex. timpul de prelucrare).

Pentru a putea determina care repere sunt reprezentative se va utiliza analiza ABC, la care criteriul va fi considerat timpul anual de prelucrare:

Unde:

j - indicele reperului ( j = 1 15 );

i - indicele operatiei ( i = 1 .. 5 );

SAF_j - seria anuala de fabricatie pentru j;

t_i - timpul de prelucare a operatiei i.

A = 0% - 65%

B = 65% - 90%

C = 90% - 100%

Nucleul tipologic va fi alcatuit din reperele cuprinse in clasa A.

Pentru a putea compara intre ele reperele din nucleul tipologic, deoarece caracteristicile acestora au unitati de masura diferite, acestea trebuie aduse la un numitor comun. Astfel se va apela la teoria utilitatilor, in care se va tine cont doar de reperele care fac parte din nucleul tipologic (cele care sunt din clasa A).

Teoria utilitatilor consta in inlocuirea valorilor concrete ale caracteristicii reperului cu anumite utilitati. Situatia cea mai favorabila se va considera ca fiind 1 iar situatia cea mai nefavorabila egala cu 0. Pentru celelalte valori se vor aplica urmatoarele formule:

Daca situatia favorabila este egala cu valoarea maxima atunci

Daca situatia favorabila este egala cu valoarea minima atunci

max, min - valorile maxime si minime din cadrul criteriului

a_k - valoarea concreta a reperului pentru criteriul considerat

Inmultind valorile utilitatilor cu valorile coeficientilor de importanta aferenti criteriilor si insumand aceste produse se va obtine o nota care va caracteriza din punct de vedere global a tuturor criteriilor considerate reperul respectiv (insumarea produselor se aplica pentru un singur reper):

i - indicele criteriului;

j - indicele reperului;

k_i - coeficientul de importanta pentru criteriul i;

u_ij - utilitatile pentru reperul j si criteriul i.

Facand diferenta intre notele a 2 repere se vor obtine coeficientii de concordanta si care reprezinta masura efortului de flexibilitate a sistemului.

Pentru realizarea matricei de concordanta se foloseste relatia:

g,h - indicii reperelor intre care se realizeaza concordanta

i - indicele criteriului

- diagonala principala va fi intotdeauna 0

- aceasta este simetrica in raport cu diagonala principala

Cu cat valorile cuprinse in aceasta matrice sunt mai mici cu atat efortul sistemului de a se adapta la prelucrarea diverselor repere este mai mic.

In continuare se trece de la matricea coeficientilor de concordanta la matricea coeficientilor de afinitate.

1.Analiza ABC a sarcinii de productie

Lungimea semifabricatului se calculeaza din tabel ca suma a valorilor corespunzatoare timpilor de prelucrare de pe linia reperului respectiv si se exprima in mm.

L = t₁ + t₂ + t₃ + t₄ + t₅

L_R1 = 5 +20 + 36 + 34 = 95 [mm]

L_R2 = 5 + 17 + 18 + 33 = 73 [mm]

L_R3 = 5 + 69 + 14 + 59 + 25 = 172[mm]

L_R4 = 5 + 59 + 71 + 92 + 38 = 265 [mm]

L_R5 = 5 + 24 + 79 + 24 + 29 = 161 [mm]

L_R6 = 5 + 63 + 33+ 12+ 23 = 136 [mm]

L_R7 = 5 + 65 + 60 + 26 = 156 [mm]

L_R8 = 5 + 45 + 27 + 55 + 29 = 161 [mm]

L_R9 = 5 + 20 + 49 + 21 = 95[mm]

L_R10 = 5 + 43 + 12 + 24 = 84 [mm]

L_R11 = 5 + 92 + 46 + 14 +28 = 185 [mm]

L_R12 = 5 + 48 + 18 + 39 = 111 [mm]

L_R13 = 5 + 48 + 75 + 23 = 151 [mm]

L_R14 = 5 + 17 +75 + 13 + 31 = 141 [mm]

L_R15 = 5 + 16 + 77 + 37 = 135 [mm]

Diametrul semifabricatului la pornire (D_max) se determina din tabel ca valoarea maxima corespunzatoare timpilor de prelucrare de pe linia reperului respectiv si se exprima in mm.

D_R1 = 36 [mm]

D_R2 = 33 [mm]

D_R3 = 69 [mm]

D_R4 = 92 [mm]

D_R5 = 79 [mm]

D_R6 = 63 [mm]

D_R7 = 65 [mm]

D_R8 = 55 [mm]

D_R9 = 49 [mm]

D_R10 = 43 [mm]

D_R11 = 92 [mm]

D_R12 = 49 [mm]

D_R13 = 75 [mm]

D_R14 = 31 [mm]

D_R15 = 77 [mm]

Greutatea bruta a reperului se calculeaza considerandu-se ca semifabricatul de pornire este cilindric cu dimensiunile L si D_max determinate anterior, iar densitatea materialului(otel) este 7.8 g/cm³.

V = ∏ * R² *L; G = V * ρ

V - volumul cilindrului

R - raza bazei cilindrului

G_R1 = ∏ * (3.6² /4) * 9.5*7.8 = 753.86 ;            G_R1 = 753.86 * 10^-6 = 0.753 [kg]

G_R2 = ∏ * (3.3² /4) * 7.3*7.8 = 486.76 ; G_R2 = 486.76 * 10^-6 = 0.486 [kg]

G_R3 = ∏ *( 6.9²  /4) * 17.2*7.8 = 5014.07 ; G_R3 = 5014.07 * 10^-6 = 5.014kg]

G_R4 = ∏ * (9.2² /4)* 26.5*7.8 = 13733.64 ;      G_R4 = 13733.64 * 10^-6 = 13.733 [kg]

G_R5 = ∏ *( 7.9² /4)* 16.1*7.8 = 6152.39 ;        G_R5 = 6152.39 * 10^-6 = 6.152 [kg]

G_R6 = ∏ * (6.3² /4) * 13.6*7.8 = 3305.09 ; G_R6 = 3305.09 * 10^-6 = 3.305 [kg]

G_R7 = ∏ * (6.5² /4)* 15.6*7.8 = 435.66 ; G_R7 = 435.66 * 10^-6 = 4.356 [kg]

G_R8 = ∏ * (5.5 ² /4)* 16.1*708 = 2889.44 ; G_R8 = 2889.44 * 10^-6 = 2.889 [kg]

G_R9 = ∏ * (4.9² /4)*9.5*7.8= 1396.62 ; G_R9 = 1396.62 * 10^-6 = 1.396 [kg]

G_R10 = ∏ * (4.3² /4)*8.4*7.8 = 950.99; G_R10 = 950.99 * 10^-6 = 0.950[kg]

G_R11 = ∏ * (9.2² /4) *18.5*7.8 = 9587.6 ;G_R11 = 9587.6 * 10^-6 = 9.587 [kg]

G_R12 = ∏ * (4.9 ² /4)*11.1*7.8 = 1631.84 ; G_R12 =1631.84* 10^-6 = 1.631 [kg]

G_R13 = ∏ * (7.5² /4)*15.1*7.8 = 5200.7 ;G_R13 = 5200.7 * 10^-6 = 5.2 [kg]

G_R14 = ∏ * (3.1² /4)*14.1*7.8 = 829.67 ;G_R14 = 829.67 * 10^-6 = 8.29 [kg]

G_R15 = ∏ * (7.7² /4) *13.5*7.8 = 4900.94 ;   G_R15 = 4900.94 *10^-6 = 4.9 [kg]

Seria anuala de fabricatie se calculeaza din tabel ca suma a valorilor timpilor de prelucrare de la primele 4 operatii inmultita cu valoarea timpului de prelucrare de la operatia 5 si se exprima in buc/an.

SAF_R1 = (5 + 20 + 36 ) * 34 = 2075 [buc/an]

SAF_R2 = (5 + 17 + 18) * 33 = 1320 [buc/an]

SAF_R3 = (5 + 69 + 14 + 59) * 25 = 3675 [buc/an]

SAF_R4 = (5 + 59 + 71 + 92) * 38 = 8626 [buc/an]

SAF_R5 = (5 + 24 + 79 + 24) * 29 = 3828 [buc/an]

SAF_R6 = (5 + 63 + 33+12 ) * 23= 2599 [buc/an]

SAF_R7 = (5 + 65 + 60) *26 = 3580 [buc/an]

SAF_R8 = (5 + 45 + 27 + 55) * 29 = 3828 [buc/an]

SAF_R9 = (5 + 25 + 49) * 21 = 1659 [buc/an]

SAF_R10 = (5 + 43 + 12) * 24 = 1440 [buc/an]

SAF_R11 = (5 + 92 + 46 + 14) * 28/ = 4396 [buc/an]

SAF_R12 = (5 + 49+ 18) * 39 = 2808 [buc/an]

SAF_R13 = (5 + 48 + 75) * 23 = 2944 [buc/an]

SAF_R14 = (5 + 17 + 75 + 13) * 31 = 3410 [buc/an]

SAF_R15 = (5 + 16 + 77) * 37 = 3626 [buc/an]

Principalele valori de calcul a reperelor

Timpul de prelucrare se calculeaza cu relatia:

T = SAF * (t₁ + t₂ + t₃ + t₄ + t₅) = S * L [min/an]

T_R1 = 2075* 95 = 197125[min/an]

T_R2 = 1320 * 73 = 96360 [min/an]

T_R3 = 3675 * 172 = 225342 [min/an]

T_R4 = 8626 * 265 = 2285980 [min/an]

T_R5 = 3828 * 161 = 616308min/an]

T_R6 = 2599 * 136 = 253464 [min/an]

T_R7 = 3380 * 156 = 527280 [min/an]

T_R8 = 3828 * 161 = 616308 [min/an]

T_R9 = 1659 * 95 = 157605 [min/an]

T_R10 = 1440 * 84 = 120960 [min/an]

T_R11 = 4392 * 185 = 812520 [min/an]

T_R12 = 2808 * 111 = 311688 [min/an]

T_R13 = 2944 * 151 = 444544 [min/an]

T_R14 = 3410 * 141 = 480810 [min/an]

T_R15 = 3626 * 135 = 489510 [min/an]

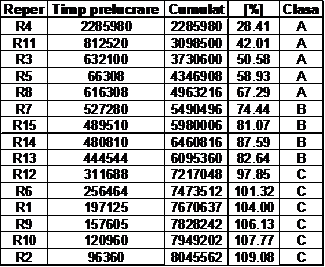
Analiza ABC

In urma analizei ABC rezulta ca nucleul tipologic este format din 4 repere si anume: R4, R11, R3, R5, R8.

2. Determinarea matricii coeficientilor de concordanta

Efortul de trecere al sistemului de la un produs la altul il corelam cu deosebirea/apropierea dintre tipurile de repere. Descriem fiecare tip de reper cu ajutorul unor criterii semnificative: lungime, greutate, rigiditate si le aducem la un numitor comun printr-un indicator global.

Valorile reperelor de clasa A

Pentru a aduce la numitor comun cele 3 criterii, exprimate in unitati de masura diferite, folosim teoria utilitatilor. Stabilim utilitatea 1 pentru cea mai favorabila situatie in cadrul fiecarui criteriu si utilitatea 0 pentru extrema cealalta. Valorile intermediare vor fi marcate cu utilitati intre 0 si 1 prin interpolare liniara.

Utilitatile se calculeaza cu formula: si se obtin urmatoarele valori:

Valorile reperelor de clasa A

transformate in valori unitare

Calculul notei:

N_R4 = 0.3 * 1 + 0.3 * 0.05 + 0.4 * 0.97 = 0.7

N_R6 = 0.3 * 1 + 0.3 * 1 + 0.4 * 0 = 0.6

N_R11 = 0.3 * 0.63 + 0.3 * 0.72 + 0.4 * 0.77 = 0.71

N_R5 = 0.3 * 0.61 + 0.3 * 0.8+ 0.4 * 0.47 = 0.61

N_R9 = 0.3 * 0.96 + 0.3 * 0 + 0.4 * 1 = 0.69

N_R10 = 0.3 * 0 + 0.3 * 0.92 + 0.4 * 0.68 = 0.55

Coeficientii de concordanta sunt:

C_R4R4 = 0

C_R4R6 = 0.3 * |1 - 1| + 0.3 * |0.05 - 1| + 0.4 * |0.97 - 0| = 0.67

C_R4R11 = 0.3 * |1 - 0.63| + 0.3 * |0.05 - 0.72| + 0.4 * |0.97 - 0.77| = 0.39

C_R4R5 = 0.3 * |1 - 0.61| + 0.3 * |0.05 - 0.8| + 0.4 * |0.97 - 0.47| = 0.54

C_R4R9 = 0.3 * |1 - 0.96| + 0.3 * |0.05 - 0| + 0.4 * |0.97 - 1| = 0.04

C_R4R10 = 0.3 * |1 - 0| + 0.3 * |0.05 - 0.92| + 0.4 * |0.97 - 0.68| = 0.68

C_R6R6 = 0

C_R6R11 = 0.3 * |1 - 0.63| + 0.3 * |1 - 0.72| + 0.4 * |0 - 0.77| = 0.50

C_R6R5 = 0.3 * |1 - 0.61| + 0.3 * |1 - 0.8| + 0.4 * |0- 0.47| = 0.37

C_R6R9 = 0.3 * |1 - 0.96| + 0.3 * |1 - 0| + 0.4 * |0 - 1| = 0.71

C_R6R10 = 0.3 * |1- 0| + 0.3 * |1 - 0.92| + 0.4 * |0 - 0.68| = 0.60

C_R11R11 = 0

C_R11R5 = 0.3 * |0.63 - 0.61| + 0.3 * |0.72 - 0.8| + 0.4 * |0.77 - 0.47| = 0.15

C_R11R9 = 0.3 * |0.63 - 0.96| + 0.3 * |0.72 - 0| + 0.4 * |0.77 - 1| = 0.41

C_R11R10 = 0.3 * |0.63 - 0| + 0.3 * |0.72 - 0.92| + 0.4 * |0.77 - 0.68| = 0.29

C_R5R5 = 0

C_R5R9 = 0.3 * |0.61 - 0.96| + 0.3 * |0.8 - 0 | + 0.4 * |0.47 - 1| = 0.56

C_R5R10 = 0.3 * |0.61 - 0| + 0.3 * |0.8 - 0.92| + 0.4 * |0.47 - 0.68| = 0.30

C_R9R9 = 0

C_R9R10 = 0.3 * |0.96 - 0| + 0.3 * |0 - 0.92| + 0.4 * |1 - 0.68| = 0.69

C_R10R10 = 0

Matricea coeficientilor de concordanta

3.Determinarea coeficientilor de afinitate

Se trece de la matricea coeficientilor de concordanta la o alta matrice numita matricea de afinitate, eliminand simetria. Propunem valoarea 1 pentru cea mai mica valoare a coeficientului de concordanta de pe linia respectiva si continuand in ordinea crescatoare a valorii coeficientilor de concordanta obtinem "matricea clasamentelor de preferinte", iar elementele acestei matrici se numesc coeficienti de afinitate.

Matricea coeficientilor de afinitate

F_(x) = 0.101164 + (6.257833 * x)

ρ = 0.9127901, se observa ca coeficientul de corelatie este > 0.7

4.Determinarea numarului si naturii modulelor de prelucrare din S.F.F. si a repartizarii lor spatiale

4.1. Determinarea configuratiei SFF prin modelarea matematica

Determinarea configuratiei SFF se va face prin modelarea matematica si, in acest sens, putem imagina urmatorul model de programare matematica liniara in numere intregi avand ca obiectiv stabilirea tipului si numarului de module operatie care compun SFF: min(Z) =

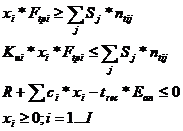
x_i - numar intreg, variabila intreaga asociata modului operatiei i;

i = 1I - indice asociat modulelor operatie delimitate pentru prelucrarea tipurilor de repere cuprinse in nucleul tipologic;

j = 1J - indice care desemneaza tipurile de repere din cadrul nucleului tipologic;

F_tpi - fondul de timp de lucru efectiv al modulului operatie, timp anual de prelucrare

F_tpi = D*S*h*60 - t_rep = D*S*h*60 - 10%*D*S*h*60 = 260*2*8*60 - 10%*260*2*8*60 = 2.25 * 10⁵ [minute];

S_j = seria anuala de fabricatie pentru reperul j;

n_tij = timpul de prelucrare a reperului j la operatia i;

K_ui - gradul minim de incarcare a modulului operatiei i;

, K_u = 75%;

nt_mas - numarul teoretic de masini (valoarea obtinuta in urma rezolvarii sistemului);

na_mas - numarul adoptat de masini (valori rotunjite ale lui X obtinute in urma rezolvarii sistemului);

R - costul celorlalte elemente componente ale sistemului (ex. transportoare piese, manipulatoare, etc.);

- costul total necesar realizat de SFF.

Ultima inecuatie din sistem reprezinta conditia de recuperare a investitiei:

c_i = pretul unui modul operatie;

- costul tuturor modulelor operatiilor;

t_rec = termenul de recuperare a investitiei (4 - 6 ani);

E_an = economiile totale realizate in urma implementarii SFF.

Centruire:

S_R4*n_t14 + S_R5*n_t15 + S_R6*n_t16 + S_R9*n_t19 + S_R10*n_t110 + S_R11*n_t111 = 4836*5 + 4185*5 + 4836*5 + 3570*5 + 3600*5 + 4608*5 = 1.28 * 10⁵ [minute/an]

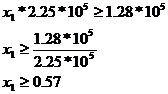
Strunjire:

S_R4*n_t24 + S_R5*n_t25 + S_R6*n_t26 + S_R9*n_t29 + S_R10*n_t210 + S_R11*n_t211 = 4836*92 + 4185*58 + 4836*94 + 3570*36 + 3600*43 + 4608*65 = 1.73 * 10⁶[minute/an]

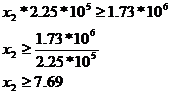
Frezare:

S_R4*n_t34 + S_R5*n_t35 + S_R6*n_t36 + S_R9*n_t39 + S_R10*n_t310 + S_R11*n_t311 = 4836*0 + 4185*47 + 4836*0 + 3570*23 + 3600*0 + 4608*0 = 2.79 * 10⁵ [minute/an]

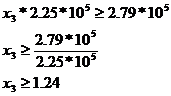
Gaurire:

S_R4*n_t44 + S_R5*n_t45 + S_R6*n_t46 + S_R9*n_t49 + S_R10*n_t410 + S_R11*n_t411 = 4836*89 + 4185*25 + 4836*87 + 3570*41 + 3600*52 + 4608*58 = 1.56 * 10⁶ [minute/an]

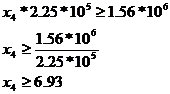
Rectificare:

S_R4*n_t54 + S_R5*n_t55 + S_R6*n_t56 + S_R9*n_t59 + S_R10*n_t510 + S_R11*n_t511 = 4836*26 + 4185*31 + 4836*26 + 3570*34 + 3600*36 + 4608*36 = 7.98 * 10⁵ [minute/an]

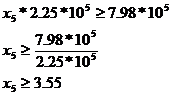
Al doilea set de inecuatii, care impun utilizarea modulelor peste un nivel K_ui considerat acceptabil, este:

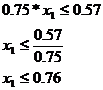
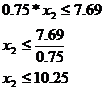
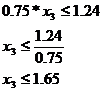
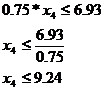
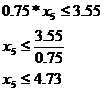
E_an = EPC + BS + EENC

EPC - economii la pretul de cost;

BS - beneficii suplimentare;

EENC - efecte economice care nu se pot cuantifica.

EPC = 4.85 * 10⁵ [lei/an]

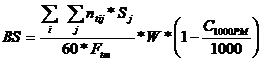
BS = 1.98 * 10⁵ [lei/an]

EENC = 175000 [lei]

E_an = 4.85 * 10⁵ + 1.98 * 10⁵ + 1.75 * 10⁵ = 8.58 * 10⁵ [lei/an]

Cu ajutorul programului STORM s-au calculat urmatoarele valori:

x₁ = 0.57x₁ = 1

x₂ = 7.69x₂ = 8

x₃ = 1.24 aproximam valorile ca nr intregi x₃ = 2

x₄ = 6.93x₄ = 7

x₅ = 3.55x₅ = 4

1.66 * (5400 * 0.57 + 28000 * 7.69 + 29400 * 1.24 + 8700 * 6.93 + 38400 * 3.55) - 5 * 8.58 * *10⁵ = 749431.9 - 4290000 = -3540568.1 < 0

1.66 * (5400 * 1 + 28000 * 8 + 29400 * 2 + 8700 * 7 + 38400 * 4) - 5 * 8.58 * 10⁵ = 834482 - 4290000 = -3455518 < 0

K_ui = 50.96 [%]

1.66 * (5400 * 1 + 28000 * 9 + 29400 * 2 + 8700 * 8 + 38400 * 4) - 5 * 8.58 * 10⁵ = 895404 - 4290000 = -3394596 < 0

Calculul robotilor in sistem

Gradul de mobilitate gm = 5 (fig. 4.4.2.)

5x

85

[puncte]

Viteza medie de amplasare pe traiectorie v_med = 0.9 [m/s] (fig. 4.4.4.)

0.9..x

2..5

[puncte]

Precizia de pozitionare Pp = +/-1 (fig. 4.4.5.)

1..4.5 [puncte]

Volumul spatiului de lucru Vsl = 10 [m³]

10.x

12.1

[puncte]

Masa maxima (= greutatea bruta maxima) mp = 11.47 [kg] (fig. 4.4.1.)

11.47x

20..0.5

[puncte]

Numar total de puncte N = 3.13 + 2.25 + 4.5 + 0.83 + 0.29 = 11 [puncte]

Costul robotului: C_R = 12.882 * N * Curs_euro / 2 = 12.882 * 11 * 4.0824 / 2 = 289.24

Structura SFF cuprinde in medie un robot la 4.38 unitati de prelucrare:

Estimare cost SFF

- unitati de lucru (masini):

1 masina de centruit1 * 5400 = 5400

8 masini de strunjit.8 * 28000 = 224000

2 masini de frezat2 * 29400 = 58800

7 masini de gaurit, alezat.7 * 8700 = 60900

4 masini de rectificat.4 * 38400 = 153600

Costul contabil al elementeleor de lucru  = 502700 lei

Partea cunoscuta (unitati de lucru, sistem de transfer, etc) reprezinta 76% din valoarea SFF:

76%502700

100%x

lei - reprezinta costul intreg al sistemului flexibil de fabricatie

Amplasarea utilajelor

Pentru amplasarea spatiala a modulelor se va folosi metoda gamelor fictive care urmareste in principal, realizarea unor fluxuri de fabricatie fara intoarceri. Modulele de prelucrare necesare pentru prelucrarea pieselor din nucleul tipologic sunt: centruirea (C), strunjirea (S), frezarea (F), gaurirea (G) si rectificarea (R).

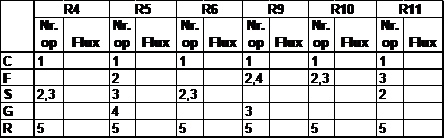
Amplasarea utilajelor

Se observa ca toate reperele au intoarceri de flux astfel incat se va aplica un algoritm de eliminare a intoarcerilor de flux.

Eliminarea intoarcerilor de flux se realizeaza prin ordonarea incarcarilor corespunzatoare numarului curent al operatiilor de-a lungul diagonalei principale. Aceasta procedura atrage divizarea modulelor de prelucrare.

Calculam in continuare incarcarile lunare si apoi le trecem in tabele:

incarcarea lunara la centruire:

operatia 1 C₁ = SAF₄ * nt₄ + SAF₅*nt₅ + SAF₆*nt₆ + SAF₉*nt₉ + SAF₁₀*nt₁₀ + SAF₁₁*nt₁₁ = 4836 * 5 + 4185 * 5 + 4836 * 5 + 2288 * 5 + 3570 * 5 + 3600 * 5C₁ = 116575 [min/an]

incarcarea lunara la frezare:

operatia 2 F₂ = SAF₅*nt₅ + SAF₉*nt₉ + SAF₁₀*nt₁₀ = 4185 * 58 + 2288 * 36 + + 3570 * 43 = 478608 [min/an]

operatia 3 F₃ = SAF₁₀*nt₁₀ + SAF₁₁*nt₁₁ = 3570 * 52 + 3600 * 58 = 394440 [min/an]

operatia 4 F₄ = SAF₉*nt₉ = 2288 * 41 = 93808 [min/an]

incarcarea lunara la strunjire:

operatia 2.. S₅ = SAF₄ * nt₄ + SAF₆*nt₆ + SAF₁₁*nt₁₁ = 4836 * 92 + 4836 * 94 +    + 3600 * 65 = 1133496 [min/an]

operatia 3 S₆ = SAF₄ * nt₄ + SAF₅*nt₅ + SAF₆*nt₆ = 4836 * 89 + 4185 * 47 + 4836 * 87 =1047831[min/an]

incarcarea lunara la gaurire:

operatia 3. G₇ = SAF₉*nt₉ = 2288 * 23 = 52624 [min/an]

operatia 4. G₈ = SAF₅*nt₅ = 4185 * 25 = 104625 [min/an]

incarcarea lunara la rectificare:

operatia 5.. R₉ = SAF₄ * nt₄ + SAF₅*nt₅ + SAF₆*nt₆ + SAF₉*nt₉ + SAF₁₀*nt₁₀ + SAF₁₁*nt₁₁ = 4836 * 26 + 4185 * 31 + 4836 * 26 + 2288 * 34 + 3570 * 36 + 3600 * 36 R₉ = 717119 [min/an]

Incarcarea anuala stabilita pentru numarul adoptat de masini

Numarul teoretic de masini s-a calculat ca raportul intre incarcarea anuala si fondul de timp al masinii:

Fondul de timp = 1880 [ore/an] * 60 = 112800 [min/an]

Impartirea incarcarilor operatiei pe mai multe module

1.66 * (5400 * 2 + 28000 * 10 + 29400 * 20 + 8700 * 2 + 38400 * 7) - 5 * 8.58 * 10⁵ = 1933900 - 4290000 = -2356100 < 0

Reprezentand acum din nou fluxurile pentru cele 6 repere din nucleul tipologic, se constata ca s-au eliminat intoarcerile de flux.

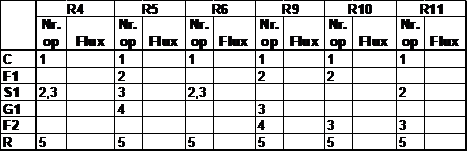
Eliminarea intoarcerilor de flux

Verificarea dinamica a configuratiei SFF

Functionarea reala a unui SFF presupune intrari aleatoare in sistem (functionare dinamica), iar noi pana acum nu am tinut seama de acest lucru. Intrarile aleatoare genereaza variatii aleatoare in ocuparea modulelor din sistem si aparitia sirurilor de asteptare ceea ce presupune amenajarea unor locuri de depozitare in care sa fie stocate reperele in asteptare, pana ce ele vor fi prelucrate. Se impune deci o regandire a amenajarii suprafetei ocupate de SFF. In cazul studiului dinamic, fiecare modul reprezinta un sistem de asteptare, iar, impreuna alcatuiesc o retea de sisteme de asteptare. Trebuie sa verificam daca la nivelul fiecarui modul:

fluxul de intrare in modul (sistem de asteptare) este de tip Poisson;

timpul de servire are repartitie exponential negativa.

Numarul mediu de intrari in SFF: - un modul lucreaza 1880 [ore/an]

[buc/ora]

Determinarea ponderilor iesirilor din fiecare modul in raport cu cantitatea totala de repere care trece prin modulul respectiv:

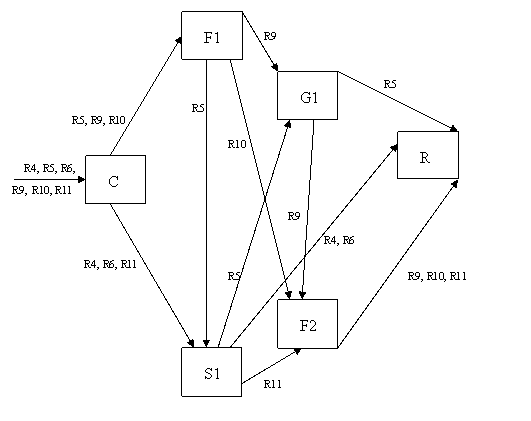
Fig. 1 Reprezentarea intrarilor si iesirilor din fiecare modul

C - F1 =

C - S1 =

F1 - S1 =

F1 - G1 =

F1 - F2 =

S1 - G1 =

S1 - F2 =

S1 - R =

G1 - F2 =

G1 - R =

F2 - R =

In sistemul nostru reperele vor strabate reteaua dinspre sursa C spre destinatia R pe diferite drumuri potrivit tehnologiei lor de prelucrare.

Fiecare sistem de asteptare este caracterizat prin parametrul intrarilor λ si parametrul servirilor μ, care este nr. mediu de unitati servite (prelucrate) in sistemul de asteptare intr-un interval de timp. Pentru determinarea parametrilor λ pentru celelalte module (pentru centruire s-a calculat deja), se va aplica o procedura de calcul care consta in generarea unei matrici k, care are ca elemente ponderile inscrise pe arcele care leaga modulele de pe linie cu cele de pe coloana.

Matricea k

Matricea k²

Matricea k³

Matricea k⁴

Matricea k⁵

Matricea P = k + k² + k³ + k⁴ + k⁵

K_CF1 = 0.44;    K_CS1 = 0.72; K_CG1 = 0.31; K_CF2 = 0.47; K_CR = 0.70

λ_F1 = λ_C * K_CF1 = 14 * 0.44 = 6.16; λ_S1 = λ_C * K_CS1 = 14 * 0.72 = 10.08;

λ_G1 = λ_C * K_CG1 = 14 * 0.31 = 4.34; λ_F2 = λ_C * K_CF2 = 14 * 0.47 = 6.58;

λ_R = λ_C * K_CR = 14 * 0.70 = 9.8

Parametrul de servire μ [buc/ora]: μ = 60/t_med

Valorile timpilor de prelucrare pentru fiecare reper de clasa A

Determinarea caracterului servirilor in modulele SFF

Este convenabil ca timpul de prelucrare (servire) sa aiba o distributie exponential-negativa. Daca servirile sunt constante (ca si la centruire) atunci caracterul "poissonian" al fluxului de intrare se conserva si fluxul de iesire, la fel ca la servirile exponential-negative.

MODULUL C

Modulul C

;;;

;;

;

0.56 < 0.67 - rezulta ca timpul de prelucrare in modulul R este o exponentiala negativa

MODULUL F1

Modulul F1

; ;

;;

In cadrul criteriului Kolmogorov, ecartul maxim dintre functia de repartitie empirica si teoretica, trebuie comparat cu o valoare "d" care se determina astfel:

d - ecartul maxim admis intre cele 2 functii de repartitie

λ₀ - parametru din tabele (in proiect se i-a valoarea 1.63)

n - numarul de repere

0.35 < 0.94 - rezulta ca timpul de prelucrare in modulul F1 este o exponentiala negativa

MODULUL S1

Modulul S1

; ;;

;;

;

0.53 < 0.82 - rezulta ca timpul de prelucrare in modulul S1 este o exponentiala negativa

MODULUL G1

Modulul G1

;

;

0.15 < 1.15 - rezulta ca timpul de prelucrare in modulul G1 este o exponentiala negativa

MODULUL F2

Modulul F2

;;

;;

0.33 < 0.94 - rezulta ca timpul de prelucrare in modulul F2 este o exponentiala negativa

MODULUL R

Modulul R

;;;

;;

;;

;;

;

0.54 < 0.67 - rezulta ca timpul de prelucrare in modulul R este o exponentiala negativa

Determinarea loturilor optime de fabricatie

Calculul urmareste determinarea numarului de loturi dintr-un an, pentru a evita atat penuria de stoc, cat si suprastocul, si pe baza acestuia se stabileste lotul optim pentru fiecare reper.

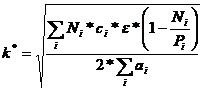
unde:

N - seria anuala

ε - rata stocarii unui leu timp de un an (se asimileaza cu rata dobanzii = 0.2)

c_i - costul reperului i

P_i - cadenta de productie a sistemului pentru reperul i

a_i - costul lansarii unui lot de piese de tip i

Costul de lansare

Media reprezinta numarul punctelor de afinitate.

a_i = nr. pct. de afinitate * costul de tranzitie = nr. pct. de afinitate * 10.5

Cadenta

Modul operatie - centruire (C)

Coeficientul fondului de timp = F_tef * n / TOTAL = 225000 * 2 / 128175 = 3.51

Modul operatie - frezare F1

Coeficientul fondului de timp = F_tef * n / TOTAL = 225000 * 5 / 526050 = 2.14

Modul operatie - strunjire S1

Coeficientul fondului de timp = F_tef * n / TOTAL = 225000 * 20 / 2246847 = 2

Modul operatie - gaurire G1

Coeficientul fondului de timp = F_tef * n / TOTAL = 225000 * 2 / 186735 = 2.41

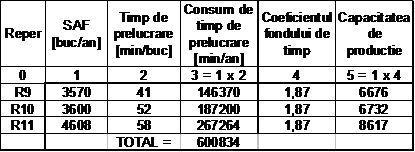
Modul operatie - frezare F2

Coeficientul fondului de timp = F_tef * n / TOTAL = 225000 * 5 / 600834 = 1.87

Modul operatie - rectificare R

Coeficientul fondului de timp = F_tef * n / TOTAL = 225000 * 7 / 798075 = 1.97

Capacitatea de productie a sistemului pentru fiecare din cele 6 repere este data de minimul capacitatilor modulelor care concura la realizarea reperelor respective. Ea reprezinta cantitatea anuala maxima din fiecare reper care poate traversa sistemul.

Reprezentarea grafica a capacitatii de productie pentru reperele de clasa A

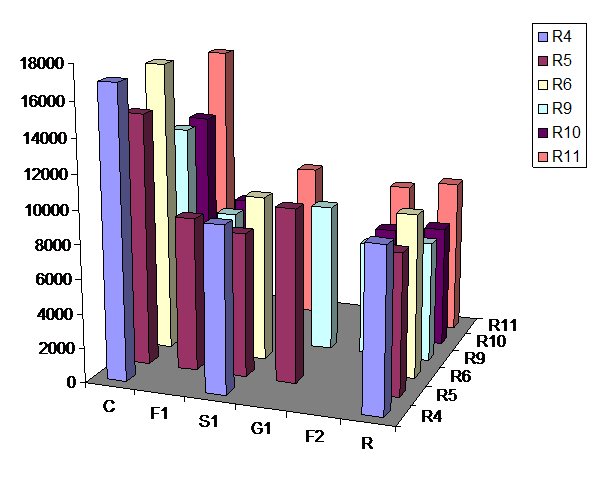
Capacitatea de productie minima pt reperul R4 este P = 9527 [buc/an]

Capacitatea de productie minima pt reperul R5 este P = 8244 [buc/an]

Capacitatea de productie minima pt reperul R6 este P = 9527 [buc/an]

Capacitatea de productie minima pt reperul R9 este P = 6676 [buc/an]

Capacitatea de productie minima pt reperul R10 este P = 6732 [buc/an]

Capacitatea de productie minima pt reperul R11 este P = 8617 [buc/an]

unde:

GB - greutatea bruta a semifabricatului de pornire pentru realizarea produsului [kg/buc]

P_m - pretul materialului [lei/kg]

T_ra - cota procentuala privind cheltuielile de transport-aprovizionare [%]

GN - greutatea neta a produsului [kg/buc]

P_des - pretul de valorificare a deseului [lei/kg]

P_m = 3.85 [lei/kg],T_ra = 0.05, P_des = 0.88 [lei/kg]

GB_R4 = G_R4 = 11 [kg]; GB_R5 = G_R5 = 3.43 [kg]; GB_R6 = G_R6 = 11.47 [kg];

GB_R9 = G_R9 = 1.4 [kg]; GB_R10 = G_R10 = 2.26 [kg]; GB_R11 = G_R11 = 4.21 [kg]

GN_R4 = GB_R4 * 0.75 = 8.25; GN_R5 = GB_R5 * 0.75 = 2.57; GN_R6 = GB_R6 * 0.75 = 8.60;

GN_R9 = GB_R9 * 0.75 = 1.05; GN_R10 = GB_R10 * 0.75 = 1.70; GN_R11 = GB_R11 * 0.75 = 3.16

M_R4 = 35.11; M_R5 = 10.95; M_R6 = 36.61; M_R9 = 5.47; M_R10 = 7.21; M_R11 = 13.44

Manopera MN:

unde:

n_ti - timpul de prelucrare la operatia i [min/buc]

St_i - salariul tarifar orar al operatiei i [lei/ora]

IMP - impozite pe salarii suportate de intreprindere [%]

CAS - cota procentuala reprezentand contributiile la fondul de asigurari sociale si la fondul de somaj [%]

MN_R5 = 0.26 * 166 = 43.16

MN_R6 = 0.26 * 212 = 55.12

MN_R9 = 0.26 * 139 = 36.14

MN_R10 = 0.26 * 136 = 35.36

MN_R11 = 0.26 * 164 = 42.64

Costul piesei de tip i este de fapt pretul de cost (PI) al reperului respectiv, calculat cu formula:

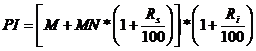
unde

M - valoarea materialului incorporat in produs [lei/buc];

MN - cheltuieli cu manopera incorporate in produs [lei/buc];

R_s - regia sectiei = 300 [%];

R_i - regia intreprinderii = 30 [%].

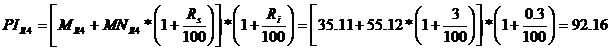PI_R5 = 55.57;   PI_R6 = 93.66; PI_R9 = 42.82; PI_R10 = 43.76; PI_R11 = 57.53

=0.2

[loturi]

Q₄ = N₄ / k = 211 [buc/lot]

Q₅ = N₅ / k = 182 [buc/lot]

Q₆ = N₆ / k = 211 [buc/lot]

Q₉ = N₉ / k = 156 [buc/lot]

Q₁₀ = N₁₀ / k = 157 [buc/lot]

Q₁₁ = N₁₁ / k = 201 [buc/lot]

Determinarea succesiunii de intrare in sistem a tipurilor de produse

Metoda componentelor tare conexe

In continuare va fi prezentata o procedura de determinare a drumului hamiltonian de lungime minima pe care o vom exemplifica pentru situatia din tabelul de mai jos.

Procedeul pe care il folosim este o euristica si in consecinta nu avem certitudinea ca solutia obtinuta va fi optima. Prima etapa a algoritmului consta in invalidarea arcelor pe care tranzitia sistemului este posibila dar cu un efort mare de flexibilitate. Presupunem ca nu exista posibilitatea tranzitiei SFF de-a lungul arcelor cu marimea mai mare decat 2, astfel reducandu-se numarul arcelor.

Matricea conexiunilor aferente

Pornind de la matricea conexiunilor se urmareste descompunerea grafului in niste subdiviziuni numite "componente tare conexe", prezentam in continuare algoritmul prin care se realizeaza gasirea componentelor tare conexe.

Construim vectorii linie respectiv coloana V1 si V1' astfel:

linia V1 se completeaza mai intai cu cifra 1 in coloanele in care exista aceasta cifra si in linia R4;

la linia V1 se aduna boolean liniile corespunzatoare numarului de coloana in care avem cifra 1 in V1;

se procedeaza identic ca la punctul anterior pe masura ce apar noi cifre de 1 in linia V1 prin adunare booleana;

in momentul in care toate pozitiile de pe linia V1 sunt 1 sau atunci cand orie noua adunare a unei linii nu mai aduce schimbariin linia V1, algoritmul de generare al liniei V1 ia sfarsit;

se procedeaza identic pentru generarea coloanei V1' dar in formularile anterioare cuvantul "linie" se schimba in cuvantul "coloana" si invers.

Componenta tare conexa care contine varful R4 se determina cu formula:

V1 =

V1' =

C1 =

Componenta tare conexa care contine varful R6 se determina cu formula:

V2 =

V2' =

C2 =

Componenta tare conexa care contine varful R11 se determina cu formula:

V3 =

V3' =

C3 =

In acest caz vom avea:

Se construieste matricea A, coloanele C1, C2 si C3 fiind obtinute prin adunarea booleana a coloanelor corespunzitoare varfurilor care sunt cuprinse in componenta respectiva. Apoi se construieste A adunand acum liniile din A pe componente. Inlocuind cu 0 elementele de pe diagonala principala a matricii A abtinem A*. Construim matricea drumurilor din graf D,

printr-o metoda similara constructiei liniilor V1.

Matricea A

Matricea A

Matricea A*

Pentru ca sa existe drum hamiltonian in graful din figura de mai sus este necesar ca, in matricea drumurilor D, numarul elementelor egale cu 1 sa fie , unde n este rangul matricii drumurilor.

Matricea D

In acest caz conditia nu este indeplinita, se observa ca varful R6 este izolat deoarece de la el nu pleaca nici un arc. In aceasta situatie introducem si virful R6 prin introducerea arcului de lungime minima care a fost eliminat si reluam algoritmul de determinare a drumului hamiltonian.

Componenta tare conexa care contine varful R4 se determina cu formula:

V1 =

V1' =

C1 =

Drumul hamiltonian este urmatorul: C1: R4->R6->R11->R5->R9->R10.

Lungimea drumului este de 5 + 2 + 1 + 5 + 4 = 17 unitati

Cuplajul maximal ca referinta pentru evaluarea calitatii solutiei

Pentru a verifica daca solutia obtinuta prin euristica 1 este optima vom utiliza in continuare algoritmul acoperirii zerourilor.

Plecand de la matricea coeficientilor de afinitate, redata mai jos vom aplica in cele ce urmeaza

algoritmul amintit.

O imagine asupra departarii de optim a solutiei gasite ne-o putem forma trecand in revista metoda cuplajului maximal.

Consideram o multime I care include tipurile de repere care intra in sistem si o alta multime II care cuprinde starile sistemului. Din I au fost trase arce spre II mai putin fata de punctul cu acelasi nume, trecand totodata cifrele de prioritate care reprezinta relatiile de preferinta ale fiecarui reper.

Redam mai jos matricea clasamentelor de preferinte si pentru a invalida relatiile intre simboluri identice, am notat cu ∞ pozitiile de pe diagonala principala.

Scadem din fiecare linie elementul cel mai mic (1). Urmarim daca au aparut zerouri si pe fiecare coloana. Daca in urma acestei proceduri putem izola un numar de zerouri egal cu rangul matricei atunci algoritmul s-a terminat.

Se observa ca se pot izola 6 zerouri. Vom completa tabelul de mai jos astfel: in loc de zerourile obtinute mai sus vom scrie valorile din matricea coeficientilor de afinitate.

Concluzie: prin euristica am obtinut o succesiune care cuprinde toate reperele inlantuite cu 6 arce in marime totala de 9 unitati.

Metoda inmultirii latine in matrici

In rezolvarea acestei probleme se pleaca de la matricea coeficientilor de afinitate.

Algoritmul de rezolvare este urmatorul:

Se invalideaza arcele mai mari decat 3

Se construieste matricea latina T dupa urmatoarea regula:

- 0 daca nu exista arc intre i si j;

- ij, daca exista arc intre cele doua varfuri.

Matricea T

Se construieste T*, eliminand din T  primul indice din grupele ij.

Matricea T ^*

Se calculeaza: pana la: unde n este rangul matricei n =7, L - inmultirea latina a matricelor.

Inmultirea latina a 2 matrici se reralizeaza exact ca inmultirea intre 2 matrici, cu respectarea suplimentara a inca 2 reguli:

in matricea produs se va trece 0 daca unul dintre termenii inmultirii este 0 daca unul dintre termenii inmultirii este 0 sau daca un se va putea obtine o succesiune de cifre independente

in matricea produs se vor trece toate succesiunile de cifre independente una sub alta.

Matricea T²

Matricea T³

Matricea T⁴

Matricea T⁵

Se calculeaza lungimea drumurilor astfel obtinute si se obtine drumul de lungime minima, si anume:

513462: R9->R4->R11->R5->R10->R6: 1 + 2 + 1 + 2 + 3 = 9 unitati

sau

624315: R10->R6->R5->R11->R4->R9: 3 + 1 +1 +3 + 1 = 9 unitati

Modelarea SFF ca joc matematic (determinarea solutiei

jucatorului minimizant)

Determinarea solutiei jucatorului minimizant

Se poate interpreta ca functionarea SFF se desfasoara in concordanta cu teoria jocurilor matematice cu suma nula. Adversarii sunt sistemul de fabricatie care tinde sa limiteze varietatea tipologica a sarcinii de productie pentru a reduce costurile de tranzitie si sarcina de productie, care tinde sa se diversifice. Sarcina de productie este jucatorul maximizant, iar sistemul flexibil de fabricatie este jucatorul minimizant.

Miza conflictului dintre cei doi jucatori este costul de tranzitie cij. In consecinta matricea jocului este chiar matricea clasamentelor de preferinte prezentate mai jos:

Solutia va materializa o situatie de echilibru care pentru un sistem va insemna o flexibilitate acceptabila, iar pentru sarcina de productie o diversificare acceptabila. Optimul este prezentat de solutia jocului care este situatia reciproc acceptabila pentru tendintele antagoniste promovate de cei doi adversari.

In urma interpretarii SFF ca joc matematic cu suma nula, solutia obtinuta va desemna tipurile de repere care se vor prelucra in SFF si frecventa cu care acestea trebuie sa apara in sistem astfel incat, costul mediu de tranzitie al sistemului sa se situeze sub o valoare de echilibru numita valoarea jocului.

In termenii teoriei jocurilor matematice, solutia obtinuta, se numeste "strategia jucatorului minimizant".

0 * x₁ + 5 * x₂ + 2 * x₃ + 3 * x₄ + 1 * x₅ + 4 * x₆ v

4 * x₁ + 0 * x₂ + 2 * x₃ + 1 * x₄ + 5 * x₅ + 3 * x₆ v

3 * x₁ + 5 * x₂ + 0 * x₃ + 1 * x₄ + 4 * x₅ + 2 * x₆ v

4 * x₁ + 3 * x₂ + 1 * x₃ + 0 * x₄ + 5 * x₅ + 2 * x₆ v

1 * x₁ + 5 * x₂ + 2 * x₃ + 3 * x₄ + 0 * x₅ + 4 * x₆ v

4 * x₁ + 3 * x₂ + 1 * x₃ + 2 * x₄ + 5 * x₅ + 0 * x₆ v

x₁ + x₂ + x₃ + x₄ + x₅ + x₆ =1

Se observa ca in inecuatii coeficientii necunoscutelor sunt coeficientii de afinitate, necunoscutele reprezinta frecventele cu care trebuie sa apara in sistem tipurile de repere, ar v este valoarea jocului. Daca operam schimbarea de variabila:

sistemul poate fi transformat intr-un model de programare matematica liniara:

0 * x₁ + 5 * x₂ + 2 * x₃ + 3 * x₄ + 1 * x₅ + 4 * x₆ 1

4 * x₁ + 0 * x₂ + 2 * x₃ + 1 * x₄ + 5 * x₅ + 3 * x₆ 1

3 * x₁ + 5 * x₂ + 0 * x₃ + 1 * x₄ + 4 * x₅ + 2 * x₆ 1

4 * x₁ + 3 * x₂ + 1 * x₃ + 0 * x₄ + 5 * x₅ + 2 * x₆ 1

1 * x₁ + 5 * x₂ + 2 * x₃ + 3 * x₄ + 0 * x₅ + 4 * x₆ 1

4 * x₁ + 3 * x₂ + 1 * x₃ + 2 * x₄ + 5 * x₅ + 0 * x₆ 1

Dupa rezolvare(cu ajutorul STORM) solutia obtinuta este:

X₁ = 0 X₂ =0 X₃ =1X₄ = 0 X₅ = 0 X₆ = 0

z = x₁ + x₂ +x₃ + x₅ +x₆ +x₇= 1

Operand in sens invers schimbarea de variabila obtinem:

V = 1 / z = 1 / 1= 1

X₁^'=0; X₂^'=0; X₃^'=1; X₄^'=0; X₅^'=0; X₆^'=0

Analiza de sensibilitate a costului mediu de tranzitie in raport cu valoarea jocului (in solutia optima a jucatorului minimizant).

CMT < V  (1)

Daca sistemul va prelucra reperul R3 cu o frecventa de 100% indiferent de numarul de tranzitii, costul mediu de tranzitie (CMT) nu va depasi valoarea jocului care este 1.