Testul mann-whitney u

TESTUL MANN WHITNEY U

Testul Mann Whitney U este asemanator in multe privinte cu testele parametrice pentru diferenta dintre mediile aritmetice a doua esantioane independente. In ambele cazuri, comparam doua esantioane independente pentru a face inferente despre diferentele dintre cele doua populatii de referinta si comparam rezultatul calcularii testului statistic cu distributia de esantionare a rezultatelor tuturor esantioanelor posibile. Pe de alta parte, acest test se bazeaza pe ordonarea scorurilor esantioanelor, astfel ca este aplicabil la date de nivel ordinal.

Ca si alte teste statistice aplicabile la date de nivel ordinal, testul Mann-Whitney U foloseste atribuirea de ranguri. A atribui ranguri unei multimi de scoruri de nivel ordinal inseamna a pune in corespondenta respectiva multime de scoruri cu numere naturale din multimea in asa fel incat succesiunea scorurilor sa se pastreze. Sa presupunem, de pilda, ca intr-un inventar de personalitate li se cere subiectilor sa evalueze o serie de propozitii dupa urmatoarea scala: Acord puternic, Acord, Nedecis, Dezacord, Dezacord puternic. Putem atribui ranguri acestor scoruri dupa cum urmeaza:

Intrucat singura semnificatie a atribuirii de ranguri este reflectarea ierarhiei scorurilor, o alta modalitate de a atribui ranguri in acest exemplu este urmatoarea:

Cu toate acestea, se obisnuieste ca diferenta dintre doua ranguri imediat succesive sa fie egala cu unitatea.

Testul Mann Whitney U comporta doua variante, in functie de dimensiunile esantioanelor. Prezentam mai intai testul pentru esantioane mici (n₁ 20 si n₂ 20).

Sa presupunem ca ne preocupa diferenta pe sexe privind nivelul de satisfactie in raport cu serviciile sociale oferite intr-un campus universitar. Pentru aceasta, selectam aleatoriu doua esantioane de studenti, baieti si fete, cu n₁ = 10 si n₂ = 10, si administram o scala in care un scor inalt indica un nivel inalt de satisfactie. Scorurile obtinute sunt prezentate in tabelul 5.

Tabelul 5 Scoruri ale satisfactiei exprimate in raport cu

serviciile sociale oferite intr-un campus universitar

Mai intai, aranjam scorurile din fiecare esantion in ordine crescatoare (sau descrescatoare). Apoi, consideram scorurile combinate ale celor doua esantioane ca si cum ar fi vorba despre un singur esantion si atribuim ranguri scorurilor combinate, de la cel mai mic la cel mai mare scor. Astfel, atribuim rangul 1 celui mai mic scor (5), rangul 2 scorului imediat urmator (9) s.a.m.d. pana la cel mai mare scor (45). Daca intalnim doua sau mai multe scoruri identice (doua sau mai multe cazuri cu acelasi scor), procedam dupa cum urmeaza:

q      consideram rangurile pe care aceste scoruri le-ar fi avut daca ar fi fost diferite si imediat succesive;

q      calculam media aritmetica a acestor ranguri;

q      atribuim fiecarui scor rangul mediu astfel obtinut.

In exemplul nostru, cazurile 8 si 17 au acelasi scor, 30. Scorului cazului 8 I-am fi atribuit rangul 14, iar scorului cazului 17 I-am fi atribuit scorul 15. Prin urmare, atribuim ambelor scoruri rangul 14,5 ((14 + 15)/2), iar scorului imediat urmator in ordine crescatoare (32) ii atribuim rangul 16 (rangul pe care l-ar fi avut acest scor, daca cele doua scoruri 30 ar fi fost diferite). Dupa aceasta operatie, calculam suma rangurilor pentru fiecare esantion. Intuitiv vorbind, daca cele doua esantioane reprezinta populatii care nu difera semnificativ intre ele sub aspectul variabilei masurate, atunci cele doua sume sunt apropiate ca valoare. Daca, insa, cele doua esantioane reprezinta populatii care difera semnificativ intre ele sub aspectul variabilei masurate, atunci cele doua sume sunt mult diferite.

Calcularea statisticii testului presupune mai intai calcularea a doua marimi statistice, U₁ si U₂, cu ajutorul urmatoarelor formule:

Formula 7

Formula 8

In aceste formule, n₁ si n₂ sunt, respectiv, dimensiunile celor doua esantioane, iar ΣR₁ si ΣR₂ sunt, respectiv, sumele rangurilor pentru cele doua esantioane.

Odata calculate cele doua marimi, U₁ si U₂, se ia drept valoare pentru U (obtinut) cea mai mica dintre valorile U₁, U₂: U (obtinut) = min (U₁, U₂).

Pentru a stabili valoarea critica din distributia de esantionare a valorilor U, folosim tabelul valorilor critice pentru testul Mann Whitney U (Anexa F). Pe primul rand si pe prima coloana din stanga ale acestui tabel sunt trecute dimensiunile a doua esantioane. Nivelele α sunt date pentru un test unilateral (directional). In cazul unui test bilateral (non-directional), nivelul α dat se localizeaza inmultind cu doi valoarea lui α. Valoarea critica, U (critic), se afla la intersectia liniei corespunzatoare dimensiunii unui esantion cu coloana corespunzatoare dimensiunii celuilalt esantion la nivelul α ales. In exemplul nostru, avand n₁ = 10 si n₂ = 10, pentru α = 0,05 (test non-directional), U (critic) = 23.

Ipoteza de nul este, ca intotdeauna, un enunt de tipul "nici o diferenta", dar este formulata in termeni mai generali decat in cazul testelor parametrice: nu exista nici o diferenta in privinta scorurilor populatiilor respective sub aspectul variabilei de interes. In exemplul nostru, ipoteza de nul enunta ca nu exista nici o diferenta intre studente si studenti sub aspectul satisfactiei exprimate in raport cu serviciile sociale oferite in campus. De regula, ipoteza alternativa enunta ca populatiile din care au fost selectate esantioanele sunt diferite sub aspectul variabilei de interes. Aceasta forma a ipotezei de nul conduce la un test nondirectional. Desigur, putem apela la un test directional, atunci cand sensul diferentei poate fi prezis, i.e. atunci cand putem prezice ca scorurile unei populatii sunt mai mari sau mai mici decat scorurile celeilalte populatii. Intr-un test nondirectional, regula de decizie este urmatoarea:

Se respinge H₀, daca U (obtinut) < U (critic)

De remarcat ca ipoteza de nul se respinge daca valoarea obtinuta este mai mica decat cea critica. Aceasta regula difera de regulile de decizie din cele mai multe teste de semnificatie, in care ipoteza de nul este respinsa daca valoarea obtinuta este mai mare decat cea critica.

Daca se poate prezice ca scorurile populatiei 1 sunt mai mari decat cele ale populatiei 2, regula de decizie este

Se respinge H₀, daca U₁ < U (critic)

iar daca se poate prezice ca scorurile populatiei 1 sunt mai mici decat cele ale populatiei 2, regula de decizie este

Se respinge H₀, daca U₂ < U (critic)

Testul formal decurge dupa cum urmeaza:

Pasul 1. Enuntarea ipotezelor

H₀: Satisfactia₁ = Satsfactia₂

H_a: Satisfactia₁ Satisfactia₂

Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice

Distributia de esantionare = Distributia U

α = 0,05 (test nedirectional)

U (critic) = 23

Pasul 3. Calcularea statisticii testului

Pasul 4. Luarea deciziei

Intrucat U (obtinut) > U (critic) (30,5 > 23), nu putem respinge ipoteza de nul. Studentele nu difera semnificativ de studenti sub aspectul nivelului de satisfactie in raport cu serviciile sociale oferite in campus (la un nivel de incredere de 95%).

Atunci cand n₁ > 20 si n₂ > 20, distributia de esantionare pentru U se apropie de distributia normala, astfel incat putem folosi tabelul scorurilor Z pentru a stabili zona critica. Luand drept cadru modelul in patru pasi, in pasul 2, distributia de esantionare este distributia Z, zona critica fiind cea marcata de Z (critic), in functie de nivelul α ales si de tipul de test (unilateral sau bilateral). Formula pentru Z (obtinut) este urmatoarea:

Formula 10

in care μ_U = media aritmetica a distributiei de esantionare a valorilor U pentru toate

esantioanele posibile

σ_U = abaterea standard a distributiei de esantionare a valorilor U pentru toate

esantioanele posibile

Valorile pentru μ_U si σ_U se calculeaza cu ajutorul urmatoarelor formule:

Formula 11

Formula 12

Prin urmare, in pasul 3 lucram cu urmatoarea formula:

Formula 13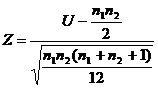

In fine, in pasul 4 se utilizeaza procedura de decizie cunoscuta pentru testul Z.