Marimi ale corelatiei la nivel de interval sau de raport

MARIMI ALE CORELATIEI LA NIVEL DE INTERVAL SAU DE RAPORT

Tehnicile statistice folosite pentru analiza corelatiei dintre variabile masurate la nivel de interval sau de raport se bazeaza pe alte concepte si modalitati de calcul fata de cele prezentate in sectiunea anterioara, dar urmaresc sa raspunda la aceleasi intrebari privind existenta, sensul si taria unei corelatii. In cele ce urmeaza, vom prezenta diagramele de imprastiere, ecuatia de regresie si coeficientul de corelatie r al ui Pearson.

Diagramele de imprastiere[1] sunt modalitati de prezentare vizuala a corelatiei dintre doua variabile masurate la nivel de interval sau de raport si sunt analoage functional tabelelor bivariate, intrucat permit sesizarea rapida a multor trasaturi importante ale unei corelatii.

Vom ilustra construirea unei diagrame de imprastiere cu ajutorul unui exemplu. Sa presupunem ca ne intereseaza daca exista o relatie intre abilitatile de limbaj si cele aritmetice pentru un esantion de 9 elevi din invatamantul primar. Rezultatele obtinute prin aplicarea testelor corespunzatoare sunt prezentate in tabelul 9.

Tabelul 9 Abilitati de limbaj si abilitati aritmetice

Pentru a construi o diagrama de imprastiere, folosim un sistem de axe rectangulare, dispunand valorile variabilei X pe axa orizontala (abscisa) si valorile variabilei Y pe axa verticala (ordonata). Ambele axe se calibreaza in unitati corespunzatoare, respectiv, scalelor de masura folosite pentru strangerea datelor. Pentru fiecare pereche de valori (pentru fiecare caz) se plaseaza un punct la intersectia perpendicularelor respective pe cele doua axe. Diagrama de imprastiere pentru datele din tabelul 9 este prezentata in figura 1.

Figura 1 Abilitati de limbaj si abilitati aritmetice

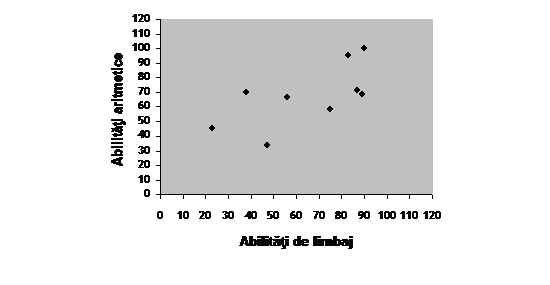
Fiecare elev este reprezentat printr-un punct plasat la intersectia celor doua scoruri obtinute de acesta. Dispunerea punctelor poate fi pusa in evidenta prin trasarea unei linii drepte care sa atinga fiecare punct sau sa treaca cat se poate mai aproape posibil de fiecare punct. Dupa cum vom vedea, aceasta linie, numita linie de regresie, poate fi descrisa precis printr-o ecuatie, dar deocamdata este suficienta trasarea sa aproximativa:

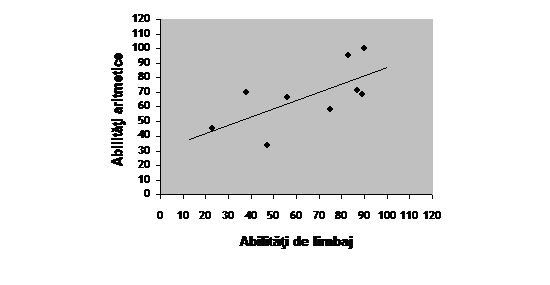
Punctele situate deasupra fiecarei valori X pot fi considerate distributii conditionate ale lui Y; cu alte cuvinte, punctele reprezinta scoruri ale variabilei Y pentru fiecare scor al variabilei X. Figura 1 arata ca aceste distributii conditionate ale lui Y se modifica dupa cum se modifica X (scorurile Y variaza in functie de scorurile X), ceea ce inseamna ca cele doua variabile sunt corelate. Existenta unei corelatii este evidentiata si de faptul ca linia de regresie formeaza un unghi cu axa X (abscisa). Daca cele doua variabile nu ar fi corelate, scorurile variabilei Y nu s-ar modifica in functie de scorurile X, astfel ca linia de regresie ar fi paralela cu abscisa.

Sensul corelatiei poate fi detectat prin panta (inclinarea) liniei de regresie fata de abscisa. In exemplul nostru avem o corelatie pozitiva, deoarece elevii cu scoruri mari in privinta variabilei X (abilitati de limbaj) tind sa aiba scoruri mari in privinta variabilei Y (abilitati aritmetice). Daca intre cele doua variabile ar fi fost o corelatie negativa, linia de regresie ar fi fost inclinata in directia opusa, indicand ca scorurile inalte ale unei variabile sunt asociate cu scoruri mici ale celeilalte variabile.

Taria corelatiei poate fi aproximativ apreciata observand imprastierea punctelor in jurul liniei de regresie. Intr-o corelatie perfecta, toate punctele s-ar afla pe linia de regresie. Prin urmare, cu cat punctele sunt mai putin imprastiate in jurul liniei de regresie, cu atat corelatia este mai puternica.

O supozitie esentiala care sta la baza tehnicilor statistice prezentate in continuare este aceea ca intre cele doua variabile considerate este o corelatie lineara, ceea ce inseamna ca dispunerea punctelor poate fi aproximata printr-o linie dreapta. Aceasta supozitie poate fi testata prin construirea unei diagrame de imprastiere inaintea aplicarii unei tehnici statistice. Daca respectiva corelatie nu este liniara, atunci supozitiile nivelului de masura de interval sau de raport nu sunt satisfacute, ceea ce inseamna ca variabilele trebuie sa fie tratate ca si cum ar fi de nivel ordinal.

Se demonstreaza ca linia care prezinta cel mai bine corelatia dintre doua variabile este descrisa de urmatoarea formula, numita ecuatia de regresie bivariata:

Formula 12

in care Y = scor al variabilei dependente

a = punctul in care linia de regresie intersecteaza axa Y

b = panta liniei de regresie

X = scor al variabilei independente

Parametrul b, numit coeficient de regresie, arata cantitatea de schimbare a lui Y care corespunde unei unitati de schimbare a lui X. Panta unei linii de regresie poate fi pozitiva, negativa sau egala cu 0. In cazul b = 0, linia de regresie este paralela cu abscisa (este orizontala), ceea ce inseamna ca intre cele doua variabile nu exista nici o corelatie. Coeficientul de regresie se calculeaza cu ajutorul urmatoarei formule:

Formula 13

in care n = numarul de cazuri

ΣXY = suma produselor dintre cele doua scoruri ale fiecarui caz

ΣX = suma scorurilor variabilei X

ΣY = suma scorurilor variabilei Y

ΣX² = suma patratelor scorurilor variabilei X

Pentru determinarea valorii coeficientului de regresie se poate folosi un tabel de calcule, ilustrat aici pentru datele din tabelul 9.

Tabelul 10 Calcule pentru coeficientul de regresie (b)

Astfel, in exemplul nostru, avem:

Aceasta valoare a parametrului b arata ca pentru fiecare unitate de schimbare a lui X, exista o crestere de 0,56 unitati in privinta lui Y. Cu alte cuvinte, o crestere cu o unitate a scorului in privinta abilitatilor de limbaj are drept rezultat o crestere cu 0,56 a scorului in privinta abilitatilor aritmetice.

Parametrul a, numit constanta de regresie, se calculeaza cu ajutorul urmatoarei formule:

Formula 14

In exemplul nostru, avem:

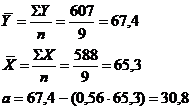
Aceasta valoare a parametrului a arata ca linia de regresie intersecteaza axa Y (ordonata) in punctul in care Y = 30,8. De notat ca a poate fi calculat si cu ajutorul urmatoarei formule, echivalenta algebric cu formula 14:

Formula 15

In fine, ecuatia de regresie pentru exemplul nostru este:

Linia de regresie poate fi folosita pentru a face predictii asupra scorului unui caz in privinta unei variabile, pornind de la scorul celuilalt caz in privinta celeilalte variabile. Daca se foloseste variabila X pentru a face predictii despre variabila Y, atunci linia de regresie este denumita regresia lui Y asupra lui X. Pentru ilustrare, sa presupunem ca, pe baza corelatiei prezentate in figura 1, ne intereseaza sa aflam scorul in privinta abilitatilor aritmetice al unui elev cu scorul 100 in privinta abilitatilor de limbaj (observati ca esantionul nu contine nici un elev cu scorul 100 la testul privind abilitatile de limbaj). Notam scorul pe care dorim sa in aflam ("scorul prezis") cu , pentru a-l distinge de scorurile Y efective. Folosind ecuatia de regresie din exemplul nostru pentru X = 100, obtinem:

Prin urmare, pe baza regresiei lui Y asupra lui X, prezicem ca un elev cu scorul 100 in privinta abilitatilor de limbaj va obtine scorul 86,8 in privinta abilitatilor aritmetice.

Coeficientul r al lui Pearson este o marime a corelatiei lineare dintre doua variabile masurate la nivel de interval sau de raport, care ia valori cuprinse intre 0 si 1. Valoarea acestui coeficient poate fi calculata cu ajutorul urmatoarei formule:

Formula 16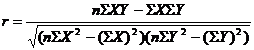

Pentru a afla valoarea coeficientului r in cazul exemplului de mai sus, folosim tabelul 10, in care am adaugat deja o coloana pentru Y² si am calculat suma corespunzatoare. Astfel, avem:

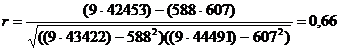
Ca si in cazul celorlalti coeficienti ai corelatiei, valorile coeficientului r diferite de 0 si de 1 nu au o interpretare directa precisa. Valorile apropiate de 0 pot fi interpretate ca indicand o corelatie foarte slaba, iar cele care se apropie de 1 ca indicand o corelatie foarte puternica. O interpretare mai directa este data de calcularea coeficientului de determinare bivariata, care este pur si simplu r². In exemplul nostru, r² = 0,435. Aceasta valoare arata ca scorurile obtinute in privinta abilitatilor de limbaj (X) explica aproximativ 43,5% din variatia totala a scorurilor obtinute in privinta abilitatilor aritmetice, restul de 56,5% din aceasta variatie datorandu-se probabil influentei altor variabile, erorilor de masurare sau intamplarii.

In conditiile in care esantionul respectiv a fost alcatuit aleatoriu, valoarea coeficientului r al lui Pearson poate fi testata pentru semnificatia la nivelul populatiei de referinta, distributia de esantionare fiind distributia t cu gl = n - 2. Calcularea statisticii testului se face cu ajutorul urmatoarei formule:

Formula 17

Daca variabilele sunt corelate la nivelul esantionului si valoarea lui t (obtinut) cade in zona critica, atunci vom respinge ipoteza de nul si vom conchide ca variabilele respective sunt corelate si la nivelul populatiei (cu probabilitatea data de nivelul α ales); daca, insa, valoarea lui t (obtinut) nu cade in zona critica, atunci nu suntem indreptatiti sa conchidem ca variabilele sunt corelate la nivelul populatiei. Intr-un astfel de caz, testul arata ca valoarea coeficientului r la nivelul esantionului poate sa apara numai datorita intamplarii, daca ipoteza de nul este adevarata, i.e. daca variabilele respective nu sunt corelate la nivelul populatiei.

Este important de retinut ca semnificatia valorii coeficientului r poate fi testata cu ajutorul formulei 6 numai daca, pe langa supoztia de linearitate a corelatiei, este satisfacuta atat supozitia ca ambele variabile au o distributie normala (distributie bivariata normala), cat si supozitia ca abaterile standard ale distributiilor conditionate ale variabilei Y sunt aproximativ egale. Pentru aceasta ultima supozitie se foloseste conceptul de homoscedasticitate. In mod obisnuit, inspectarea vizuala a unei diagrame de imprastiere este suficienta pentru a aprecia daca o corelatie se conformeaza supozitiilor de linearitate si homoscedasticitate. Dupa cum am aratat, daca dispunerea punctelor poate fi aproximata printr-o linie dreapta, atunci corelatia poate fi apreciata ca fiind lineara. Pe de alta parte, daca scorurile Y sunt relativ uniform imprastiate deasupra si dedesubtul liniei de regresie, atunci corelatia este homoscedastica. De pilda, dupa cum se poate constata imediat, corelatia prezentata in figura 1 este homoscedastica: din cele 9 cazuri, cinci se afla deasupra liniei de regresie, iar patru dedesubt.