Testul scorurilor t pentru diferenta dintre doua medii aritmetice

TESTUL SCORURILOR t  PENTRU DIFERENTA DINTRE DOUA MEDII ARITMETICE

Atunci cand abaterile standard ale populatiilor nu sunt cunoscute si esantioanele sunt mici (n₁ 30 sau/si n₂ 30), distributia de esantionare folosita este distributia t Student, cu n₁ + n₂ 2 grade de libertate. Teoretic, formula de calcul al testului scorurilor t pentru diferenta dintre doua medii aritmetice este urmatoarea:

Formula 4

Ca mai sus, termenul μ₁ - μ₂ se reduce la zero, intrucat testul are loc sub presupunerea ca ipoteza de nul, μ₁ μ₂ = 0, este adevarata. In cazul testului prezentat in aceasta sectiune, formula folosita pentru estimarea abaterii standard a distributiei de esantionare este urmatoarea:

Formula 5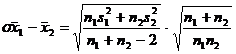

Astfel, pentru a afla valoarea lui t (obtinut) vom folosi urmatoarea formula:

Formula 6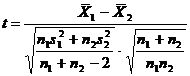

Este important de notat ca testul scorurilor t pentru doua medii aritmetice poate fi folosit doar daca cele doua populatii sunt egal dispersate sau, altfel spus, au abaterile standard egale (σ₁ = σ₂). Aceasta conditie este necesara pentru a justifica supozitia de normalitate a distributiei de esantionare si a estima abaterea standard a acesteia. Egalitatea dispersiilor poate fi testata formal[1]. Pentru scopuri practice, putem considera ca supozitia σ₁ = σ₂ este satisfacuta in masura in care esantioanele au dimensiuni apropiate[2].

Un cercetator presupune ca o anumita metoda moderna de predare a matematicii conduce la rezultate mai bune decat metodele traditionale. Pentru a verifica aceasta ipoteza, cercetatorul alcatuieste un esantion aleatoriu de 25 de elevi, pe care il imparte aleatoriu in doua grupuri. Un grup de 12 elevi este repartizat intr-o clasa in care matematica este predata dupa metoda moderna, iar celalalt grup de 13 elevi este repartizat intr-o clasa in care matematica este predata dupa metode traditionale. Dupa un an, ambele grupuri primesc acelasi test la matematica, obtinand urmatoarele rezultate:

Mediile aritmetice ale grupurilor difera in sensul prezis (μ₁ > μ₂). Aplicarea testului t arata daca aceasta diferenta este sau nu statistic semnificativa. Fie α = 0,05.

Pasul 1. Enuntarea ipotezelor

H₀: μ₁ = μ₂

H_a: μ₁ > μ₂

Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice

Distributia de esantionare = Distributia t

α = 0,05 (test unilateral)

gl = 12 + 13 2 = 23

t_α (critic) = +1,714

Pasul 3. Calcularea statisticii testului

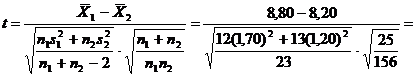
Pasul 4. Luarea deciziei

Intrucat t (obtinut) nu se afla in zona critica (+0,31 < +1,714), ipoteza de nul nu poate fi respinsa la un nivel de incredere de 95%. Diferenta dintre cele doua grupuri nu este statistic semnificativa.