Metode de calcul neparametrice

Metode de calcul neparametrice

pentru distributii diferite de cele normale.

1.     Coeficientul de asociere

Tabel de contingenta

x

+ -

+ a b

y                                              Q =

c d

Exemplu:

Din cei prezenti la curs si seminarii, 32 au trecut la examen, iar 4 nu. Din cei care nu au avut prezenta, au promovat 4 si nu au promovat 16. Sa se calculeze asocierea dintre prezenta la cursuri si promovabilitate.

X = prezenta la cursuri;

Y = promovabilitatea.

x

+ -

+ a 32 b 4

y                                             

c 4 d 16

2.     Coeficientul de concordanta

- la baza lui sta lipsa de concordanta a sensurilor abaterilor perechi.

C = , unde A = unitatile ale caror abateri perechi de la medie au

acelasi semn.

B = unitatile ale caror abateri perechi de la medie nu au

acelasi semn.

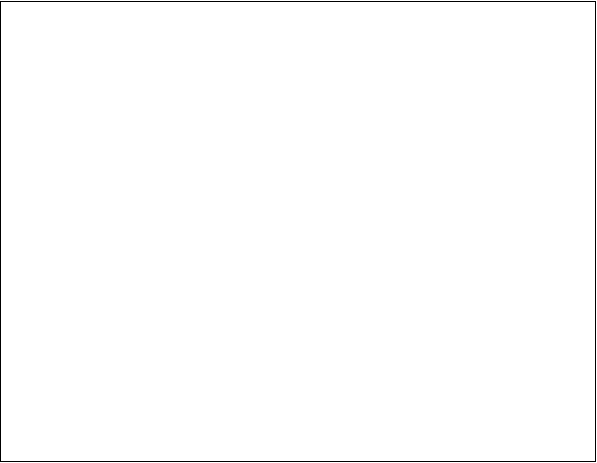
Subiecti x y Semnul diferentei fata de

1 6 8 - -

2 4 9 - +

3 9 6 + -

4 7 8 - -

5 8 10 + +

6 6 7 - -

7 5 6 - -

8 10 10 + +

9 6 8 - -

10 10 9 + +

A = 8; B=2 C=0.60;

3.     Coeficientul de corelatie reciproca PEARSON

Se foloseste in cazul cercetarii aspectelor calitative, in care distributiile cuprind mai mult de doua grupe.

Exemplu si algoritm de calcul:

Obtinand urmatoarele relatii intre prezenta la cursuri si rezultatele la examen, sa se calculeze coeficientul de corelatie reciproca Pearson.

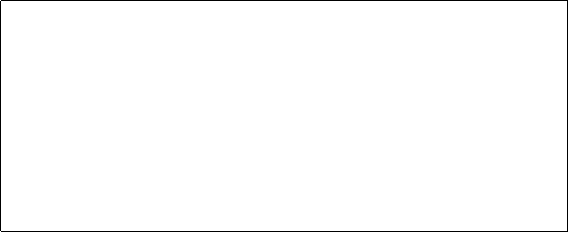Prezenta                  Rezultate Total

Slabe Medii Bune

Slaba 16 8 - 24

Medie 4 20 2 26

Buna                                - 6 18 24

Total 20 34 20 74

Algoritmul de calcul:

a)     se ridica la patrat numarul (sau frecventa) din fiecare casuta a tabelului;

b)     se inmulteste totalul de pe coloana respectiva, cu totalul de pe linia respectiva (pe care se afla casuta);

c)     se imparte a) la b);

d)     se calculeaza totalul acestor rezultate (cele de la punctul c)) - pe linie sau pe coloana;

e)     se face suma (S) acestor totaluri;

f)      se aplica formula;

4. Coeficientul de corelatie a rangurilor Spearman

. Comparatia:

A.    doua esantioane independente - se folosesc probele : proba medianei, proba secventelor, proba U sau Mann-Whitney;

B.     doua esantioane perechi - se folosesc proba semnelor si proba Wiloxon;

C.     mai multe esantioane independente - proba medianei extinsa si proba U generalizat (Kruskal-Wallis)

D.    mai multe esantioane perechi - proba Kochran si proba Freedman.

. Proba medianei

a)     nu exista valori egale cu mediana teoretica

Avem 2 grupe: A si B

A: x(=cota) 0 1 2 3 4 5 6 7 8 9 (numarul de erori)

n ( = numarul de subiecti): 3 6 3 1 0 2 3 1 0 1

B: x: 0 1 2 3 4 5 6 7 8 9

n: 2 1 1 1 3 3 1 1 2 1

Pentru a aplica proba medianei, amestecam datele de la grupa A si de la grupa B,intr-o singura distributie.

A + B x: 0 1 2 3 4 5 6 7 8 9

n: 5 7 4 2 3 5 4 2 2 2

N = 36.

Pozitia medianei = (N+1)/2 = 37/2=18.5 Mediana este 3.5.

Numarul de erori Total

Inferior medianei Superior medianei

A a 13 b 7 20

B c 5 d 11 16

Total                  18 18 36

Se transforma in c²

c²=;

Inlocuind, obtinem:

c²= 4.05; valoarea lui c² trebuie sa fie mai mare sau egala cu valoarea din tabel.

b)     exista valori egale cu mediana teoretica

Grupul de x: 3 4 5 6 7 8 9 10

control n: 2 1 3 3 2 2 1 0

Grupul x: 3 4 5 6 7 8 9 10

experimental n: 1 0 2 1 3 1 3 2

Reunim cele doua grupe x: 3 4 5 6 7 8 9 10

n: 3 1 5 4 5 3 4 2

Pozitia medianei = 14.

. Atunci cand numarul cazurilor este foarte mare:

Inferior medianei Egal medianei Superior medianei

Grupul experimental 4 3 6

Grupul de control 9 2 3

Cazul I:

Inferior sau egal medianei Superior medianei

Grupul experimental a 7 b 6

Grupul de control c 11 d 3

Cazul II:

Inferior medianei Egal sau superior medianei

Grupul experimental a 4 b 9

Grupul de control c 9 d 5

Pentru un numar mic de cazuri, se aplica o varianta, nuita varianta lui YATES.

c²=;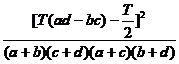

. Proba secventelor

Exemplu: Doua grupe, A si B, de cate 12 elevi. Grupul A este supus unui antrenament special. Aplicandu-se apoi un test de control, s-au obtinut urmatoarele rezultate:

A: 52 56 71 86 95 108 115 120 141 152 165 218

B: 30 45 54 74 7581 101 104 146 151 170 171

Ipoteza nula: "antrenamentul special nu are nici un efect asupra subiectilor".

.se pun datelor celor 2 grupe laolalta in ordine descrescatoare

.inlocuim in fiecare valoare cu initiala grupului din care apartine

A/ BB/ AA/ BB/ AAAA/ BB/ AA/ BBB/ A/ B/ AA/ BB/; avem, asadar, 12 secvente (r=12).

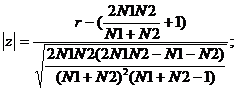
In cazul nostru,

Precizare: In grupele a si B, nu apar valori comune. Daca se intampla acest lucru, luam valorile comune o data apartinand lui A, o data ca apartinand lui B, si luam cel mai mic.

. Testul U (Mann-Whitney)

-se preteaza la date numerice, rezultate din atribuirea de puncte; este una din cele mai importante metode neparametrice, fiind oricand preferabila probei medianei.

Exemplu: Intr-o experienta de instruire, rezultatele la probele finale apar exprimate in note de la 0 la 20. In clasa experimentala (Ce) sunt 27 elevi, iar in clasa de control (Cc), tot 27 elevi.

Rezultatele sunt prezentate astfel:

Ce: x: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

n: 3 2 0 2 2 2 1 0 14 1 0 1 1 2 11 2 1

Cc: x: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

n: 3 5 3 2 3 1 0 0 1 0 0 02 1 11 1 2 0 1

Reunim cele doua grupe si acordam ranguri astfel:

Ce+Cc:x:20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1

ranguri: 1 35 7.......

-dupa ce se atribuie rangurile, se intocmeste urmatorul tabel:

Ce Cc

Subiecti

(x) Rang f R*f Rang f R*f

20                              1 1 1 1- -

19                              3 2 6 31 3

18                5 1 5 5 - -

17                              7 1 7 7 2 14

. . . .

aRf=R1=605aRf=R2=880;

-se face suma si se alege R1 sau R2, in functie de grupa mai putin numeroasa (in exemplul nostru il putem alege pe oricare, intrucat N1=N2);

-cu datele obtinute se intra in formula:

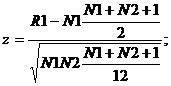
Precizare: daca in formula utilizam R2 la numarator, imediat dupa semnul "-" apare N2.

VIII.         Analiza de varianta

(ANOVA)

1.     Obiectul Anova

Problema esentiala a analizei de varianta este analiza variabilitatii, dispersiei datelor, avand surse de variatie bine precizate.

In orice cercetare de psihologie ne intereseaza sa desprindem influenta (actiunea) unor factori relevanti, cuprinsi in continurul ipotezei.

Influenta unui factor se dezvaluie in efectele sau variatiile produse asupra variabilei studiate. Noi studiem influenta fiecarui factor, suma lor, cat si efectele datorate interactiunii lor.

De obicei se lucreaza cu mai multe grupuri.

Exemple:

1.     Efectul medicamentelor asupra timpului de reactie la soferi.

Se constituie 5 grupe: G1: 10 mg

G2=20 mg

G3=30 mg

G4=40 mg

G5= grupul de control.

VI = medicamentul (administrarea lui), cu mai multe modalitati (A1,A2,A3,A4 si A0 (pentru grupul de control)).

Problema care se pune in ANOVA este compararea grupurilor intre ele.

2.     Ne propunem sa studiem influenta oboselii asupra rezultatelor invatarii (A). Avem 3 modalitati: a1:= oboseala usoara; a2 = oboseala medie; a3 = oboseala accentuata. Dar conteaza si natura materialului (B) cu doua modalitati: b1=material figural concret si b2= material pur verbal.

Pe baza acestui tip de analiza, putem observa cat din variatia unei variabile se datoreaza variatiei altei variabile si cat se datoreaza unor factori intamplatori.

De exemplu, rezultatele la invatatura se datoreaza inteligentei, dar si altor factori, cum ar fi motivatia de exemplu. Elevi cu nivelul inteligentei egal, obtin note diferite. Se impune asadar separarea influentei factorilor intamplatori de factorii esentiali.

Este evident ca trebuie luata in considerare dispersia. De exemplu daca elevii cu acelasi nivel masurat de inteligenta ar obtine toti aceeasi nota, atunci dispersia este 0.

Mai mult, daca elevii cu acelasi nivel de inteligenta obtin note intre 7 si 10, atunci inteligenta este un factor important. Daca au note intre 4 si 6, celalalt factor are mai mare influenta decat acesta.

O variabila independenta cu mai multe modalitati da doua tipuri de variatii: una intragrupala si una intergrupala. Daca variabila intragrupala este mica si variabila intergrupala este mare, atunci putem presupune ca nu apar alti factori intamplatori si abaterea fata de media generala a unui rezultat din colectia totala de date, se compune din abaterea sa fata de media grupului respectiv, la care se adauga diferenta dinte media grupului si media generala.

Ecuatia fundamentala a variabilitatii datelor etse exprimata prin suma patratelor variabilitatea totala = . Aceste formule de variabilitate se mai noteaza cu SP_totala.

SP_totala = SP_intra+SP_inter.

Pentru a calcula:

SP_totala=;

SP_inter=

, unde N = numarul total de subiecti din cele K grupuri.

; cu PM_intra si cu PM_inter se calculeaza coeficientul lui SNEDECOR.

2.     Moduri de calcul

. pentru o distributie bidimensionala

La o clasa s-au efectuat un numar de exercitii, dupa care s-a dat proba de control si s-au obtinut urmatoarele note:

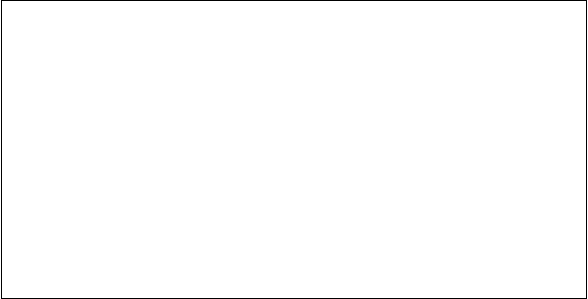
Nota obtinuta 4 5 6 7 8 910 Total

Grupul Numarul de exercitii

G1                             40 6 4 2 12

G2                             41-803 3 7 1 14

G3                             81-120 2 5 86 21

G4                             121-160 2 2 18 8 4 34

G5                             161 2 10 18 30

Total 99 1611 26 18 22 111

Algoritmul:

1. Se calculeaza mediile notelor obtinute la nivelul intregului esantion si apoi, pe cele 5 grupe, tinand cont ca cele 5 grupe sunt alcatuite pe baza numarului de exercitii.

Pentru intreg esantionul media notelor este:

X₀ =

Calculam mediile:

2. Se calculeaza dispersiile de grupe (D²_k), tot pentru aceste note, dupa formula:

D²_k=;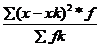

In exemplul nostru,

D₁²=

D₂²=0.816;

D₃²=0.884;

D²₄= 0.336;

D₅²=0.382.

Aceste dispersii de grup ne arata variatia caracteristicilor dependente de natura factorilor intamplatori asupra subiectilor din cadrul fiecarei grupe.

3. Se calculeaza media dispersiilor de grup (), calculata ca o medie

ponderata a dospersiilor de grupa:

= reprezinta variatia variabilei dependente pe ansamblul grupei, ca urmare a actiunii factorilor intamplatori.

4. Se calculeaza dispersia mediilor de grup fata de media generala

s²

s²= reflecta variatia caracteristicii dependente pe ansamblul grupelor, determinata de natura factorilor esentiali (VI).

Cunoscand ca mediile de grup, x_k,releva ce este esential la nivelul grupului, iar media generala (x₀) reflecta ceea ce este esential la nivelul colectivitatii generale, atunci deosebirile dintre grupe sunt concretizate de abaterile x_k-x₀.

s² reprezinta dispersia dintre grupe, sintetizeaza variatia generata de aceste deosebiri.

5. Dispersia generala (Do²) reflecta variatia caracteristicilor variabilei

dependente, generata de actiunea conjugata a celor doua grupe de factori (intamplatori si esentiali) si se aplica regula adunarii dispersiilor.

Do²=D²+s² (=3.5206)

6. Acum putem determina ponderea intensitatii variatiei aferente

fiecarei grupe de factori.

. factorii intamplatori

F₁=

. factorii esentiali

F₂=

Un caz mai complicat de ANOVA presupune variabile continue in mai multe grupuri.

Exemplu: La incheierea unei experiente efectuate cu 5 clase paralele

(A,B,C,D + E=clasa de control). S-a dat aceeasi proba finala pentru a vedea in ce masura factorul studiat influenteaza rezultatele.

Rezultatele finale sunt prezentate in urmatorul tabel de comparatie:

Clase A B C D E Total

Numarul 33 38 31 34 31 N=157

de elevi (ng)

Totalul               928 760 1013 1335748T=4784

datelor (Tg)

Totalul

patratelor (ax²) 28030 22750 35287 56637 21336Sax²=164 040

SP_inter= =

=4519.30;

SP_totala=ax²;

SP_intra= SP_totala-SP_inter= 18256.12-4519.30= 13745.82;

Se calculeaza patratul mediu (PM) inter si intra.

PM_inter=

PM_intra=

raportul Snedecor; cu acest raport se intra in tabel. Veem astfel ca ipoteza noastra nula este infirmata; factorul de diferentiere este puternic semnificativ.

Pana aici a fost vorba de o analiza globala (etapa F_omnibus). Daca raportul Snedecor era mai mic decat p=0.05, nu acceptam ipoteza nula.

Nu ni se spune intre ce grupe diferentele sunt semnificative. De asemenea, variabila independenta poate avea mai multe modalitati. Nu ni s-a spus, pana acum, care dintre modalitatile variabilei independente are efecte mari si care are consecinte minore.

Studiul continua daca raportul Snedecor este semnificativ.

Analiza continua in doua strategii:

in functie de categoriile de situatii

in functie de problemele ce trebuie rezolvate.

XI.

Problemele de tip a sau probleme pentru estimarea diferentierii sau omogenitatii, obtinute intr-o masurare - cu ajutorul coeficientului de corelatie intraclasa r.

Exemplu: In cautarea unui criteriu profesional s-au ales la intamplare dintr-un atelier 7 operatori. Acestia au fost cronometrati asupra unei operatii in momente luate la intamplare, fiecare de 28 de ori.

Prin aceasta masuratore, diferentiem sau nu operatorii intre ei?

Daca intre operatori exista diferente de randament profesional, atunci masuratoarea trebuie sa dea diferente intre ei. Vrem sa vedem, prin urmare, daca masuratoarea este valida.

Pasi:

1.     Se calculeaza testul global de varianta F.

2.     Se calculeaza coeficientul de varianta intragrupala (v_e

v_e = ;

Se calculeaza varianta intergrupe, v_g.

v_g =

Daca datele referitoare la un operator vor fi compacte (v_e este mic, iar v_g este destul de mare), atunci masuratoarea noastra a diferentiat bine muncitorii.

3.     Se pot folosi urmatorii doi indicatori:

q = ; daca q este ridicat, atunci avem diferentiere buna intre muncitori; daca q este scazut omogenitatea este foarte ridicata.

r = ; r variaza intre 0 si 1. Pentru ca masuratoarea sa fie fidela, r trebuie sa fie mai mare decat 0.70.

In probleme de omogenitate se cere ca ipoteza nula sa nu fie infirmata, iar r sa fie destul de mic.

Probleme de tip b - cand avem o colectie sistematica de grupe independente si se pune problema unor comparatii multiple.

Pentru testele de comparatie multipla:

1.     Alcatuirea tabelului pentru stabilirea semnului coeficientilor.

Comparatii intre medii Coeficientii

(grupe) a1 a2 a3

m1 cu m2                              +1 -1 0

m1 cu m3                              +1 0 -1

m2 cu m3                              0 +1 -1

m1 cu m2+m3 +2 -1 -1

m2 cu m1+m3 -1 +2 -1

Efectivele trebuie sa fie egale; grupa pe care o comparam primeste coeficienti pozitivi, iar grupa cu care comparam - coeficienti negativi.

2.     Se trece la algoritmul de calcul:

a)     utilizand totalurile

Se pleaca de la urmatorul tabel:

n=10

Grup A B C D

Total erori 92 81 64 108

(Tg)

Totalul

patratelor 897 965 780 862

a(x²))

. Se intocmeste tabelul cu datele de baza pentru analiza de varianta:

SURSA               v'/v Suma patratelor PM F

Intergrupe 3 102.27 34.3 ?

Intragrupe 36 425.50 11.8 ?

Total                                39 528.37 46.1 ?

Unde v=k-1; v' = N-k.

. Se trece la efectuarea comparatiilor. De exemplu, vom compara grupele A+D cu B+C. in acest sens, trebuie calculat indicatorul D.

D =

D1 = 92*(+1)+81*(-1)+64*(-1)+108*(+1)=55;

Se calculeaza PM_inter =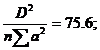

F = semnificativ la p=0.05;

b)     utilizand mediile

PM_inter (d) =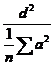

Se pleaca de la medii; in rest, se calculeaza la fel ca mai sus.

Plan bifactorial

In planurile bifactoriale ne intereseaza analiza pe linii si pe coloane.

Exemplu: S-a studiat influenta unor metode de instruire asupra coeficientului de inteligenta (C.I.)

A

I II III Total

Grupul I 114 96 74 284

(C.I. peste medie) 1116 814 542 2742

B                 

Grupul II 88 70 47 205 (C.I. sub medie) 700 462 237 1399

Total 202 166 121 489 (T)

1816 1276779 3871 (Sax²)

In fiecare casuta din tabel pe prima linie este reprezentat Tg, iar pe cea de-a doua, ax².

Intr-un astfel de experiment bifactorial, o studiere globala a variabilitatii intergrupe nu prezinta interes. Ne intereseaza comparatiile intre coloane pentru a desprinde efectele modalitatilor variabilei A, comparatiile intre linii pentru a releva efectul variabilei B, studiul interactiunii dinte A si B.

SP_totala = Sax² -

SP_inter =

SP_intra = SP _totala - SP_inter = 325.69;

. Variabilitatea intergrupe se desface intre componentele principale:

Prima componenta: pe coloane pentru variabila A;

A doua componenta: pe linii pentru variabila B;

A treia componenta: efectul combinatiei AxB.

. SP_A== 137.23;

. SP_B= 86.68;

. Efectul interactiunii: SP_AxB = SP _inter- SP_A - SP_B=0.28.

Pasul urmator: Se calculeaza mediile:

PM_A= = 68.62, unde c= numarul de coloane.

PM_B=, unde r = numarul de linii;

PM_AxB=

. Se calculeaza PM_intra =

. Calculam rapoartele Snedecor (F)

F_A=, p=0.01

F_B=, p=0.01

F_AxB=, nesemnificativ.

ANOVA se poate aplica si pentru colectivitati de k esantioane perechi. Si aici se aplica un procedeu algoritmizat, numit procedura lui Abdi.

Exemplu: Efectul medicamemtelor asupra timpului de reactie.

Conditii experimentale Total

Subiecti                          Drog A Placebo Drog B

S1 165 231 217 613

S2 172 219 217 608

S3 109 199 243 591

S4 197 219 160 576

S5 199 247 162 608

S6 193 245 191 629

Total:                              1035 1360 1190 3585

Procedeul lui Abdi presupune urmatorii pasi:

1.     Calcularea lui T.

2.     Calcularea ax² = 735 819 . Notam cu AS

3.     Se calculeaza =762 820.8. Se noteaza cu A

4.     Se calculeaza =715 371.7 Notam cu S

5.     Se calculeaza = 714 012.5. Notam cu 1.

6.     SP_totala= AS - 1 = 21 806.5;

7.     SP_intercoloane= A - 1= 8808.3;

8.     SP_interlinii= S - 1 = 1359.2;

9.     SP_intra=AS - S - A + 1 = 11739;

Cu aceste date se intocmeste tabelul ANOVA:

SURSA  v SP PM F

Coloane      2 8808.3 4404.15 ?

(medicamentele)

Linii              5 1359.2 271.84 ?

(subiectii)

Reziduu      10 11639 1163.90 ?

Total           17 21806.5 5839.89

Unde, V_coloane= numarul de coloane - 1 = 2

V_linii = numarul de linii - 1 = 6-1 = 5

Reziduu = V_liniix V_coloane = 10.

Pentru a obtine PM, se imparte SP la v.

Se trece la diferite tipuri de comparatii. Comparam Placebo cu medicamentele D1 = 1035*(-1)+1360*(+2)+1190*(-1)=495;

PM_inter(D) =

F = medicamentele au efect asupra timpului de reactie.