
|
|
|
TESTUL ITERATIILOR
Testul iteratiilor este similar ca logica si forma cu testul Testul Mann Whitney U. Ipoteza de nul enunta ca nu exista o diferenta semnificativa intre populatiile de referinta sub aspectul variabilei de interes. Pentru a aplica acest test, se combina scorurile celor doua esantioane, dupa care aceste scoruri se ordoneaza crescator (sau descrescator) ca si cum ar fi vorba despre un singur esantion. Daca ipoteza de nul este adevarata, atunci scorurile vor fi foarte amestecate si vom avea multe iteratii. O iteratie (repetare) este orice succesiune de R elemente de acelasi fel, cu R 1. Daca ipoteza de nul este falsa, populatiile fiind diferite sub aspectul variabilei de interes, atunci vor fi foarte putine iteratii.
Pentru a ilustra notiunea de iteratie, sa consideram datele din tabelul 5 si sa folosim F pentru studente si B pentru studenti. Obtinem urmatoarele iteratii:
F F B F F F F B B F B B B B F BFBFB
1 2 34 5 6 7 8 9 10 11 12
Cele doua litere F din extrema stanga reprezinta doua studente care au cele mai mici scoruri din ambele esantioane; urmatoarea litera, B, reprezinta un student cu scorul urmator in ordine crescatoare s.a.m.d. De notat ca nici o iteratie alcatuita din elemente de un anumit tip nu se invecineaza cu o iteratie alcatuita din elemente de acelasi tip. Daca, de pilda, am considera primul element al iteratiei 3 drept o iteratie distincta, atunci aceasta s-ar invecina la dreapta cu o iteratie alcatuita din elemente de acelasi tip, F.
Diferenta dintre esantioane, si deci dintre populatii, este cu atat mai semnificativa, cu cat numarul de iteratii este mai mic. Cel mai mic numar de iteratii posibil este, desigur, 2. In exemplul de mai sus, daca toti studentii ar exprima o satisfactie mai mare decat studentele in raport cu serviciile sociale din campus, am fi obtinut urmatoarele doua iteratii:
B B B B B B B B B B F F F F F F F F F F
1 2
Evident, numarul maxim posibil de iteratii este egal cu numarul de cazuri din cele doua esantioane.
Este important de retinut ca in aplicarea acestui test, cazurile care nu fac parte din acelasi esantion si au scoruri identice pot crea probleme serioase, deoarece numarul de iteratii poate fi mult afectat de felul in care sunt aranjate cazurile cu scoruri identice. Daca intalnim multe cazuri cu scoruri identice in esantioane diferite este recomandabil sa folosim alt test de semnificatie.
Distributia de
esantionare pentru iteratii aproximeaza normalitatea. Media
aritmetica a acestei distributii (![]() ) si abaterea sa standard (
) si abaterea sa standard (![]() ) se calculeaza cu ajutorul urmatoarelor formule:
) se calculeaza cu ajutorul urmatoarelor formule:
Formula 15 ![]()
Formula 16 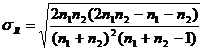
Statistica testului iteratiilor, Z (obtinut), se calculeaza cu urmatoarea formula:
Formula 17 ![]()
in care R = numarul de iteratii.
Pentru a ilustra aplicarea acestui test, sa presupunem ca doua esantioane aleatorii alcatuite, respectiv, din barbati si femei au fost chestionate cu privire la atitudinea fata de politica si politicieni. Scorurile sunt prezentate in urmatorul tabel:
Barbati
Femei
Cazul
Scorul
Cazul
Scorul
1
1
21
0
2
1
22
0
3
2
23
4
4
2
24
4
5
3
25
6
6
5
26
6
7
5
27
8
8
7
28
12
9
9
29
12
10
10
30
13
11
10
31
14
12
15
32
16
13
17
33
16
14
17
34
21
15
18
35
21
16
19
36
21
17
20
37
25
18
22
38
26
19
22
39
27
20
23
40
27
Sa observam ca aici nu exista scoruri identice in esantioane diferite (scorurile identice in acelasi esantion nu au nici o influenta asupra numarului de iteratii). Folosind tot literele B si F, obtinem urmatoarele iteratii:
F F B B B B B F F B B F F B F B B B F F F F B F F
1 2 345 67 8 9 10 11
B B B B F F F B B B F F F F
12 13 14 15
In aceste date se afla 15 iteratii si putem acum sa aplicam testul formal pentru semnificatie.
Pasul 1. Enuntarea ipotezelor
H0: Atitudinea1 = Atitudinea2
Ha: Atitudinea1 Atitudinea2
Distributia de esantionare = Distributia Z
α = 0,05
Z (critic) = 1,96
Pasul 3. Calcularea statisticii testului
![]()
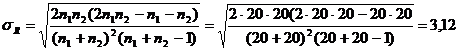
![]()
Pasul 4. Luarea deciziei
Intrucat Z (obtinut) > Z (critic) ( 1,92 > 1,96), rezultatul statisticii testului nu cade in zona critica. Prin urmare nu putem respinge ipoteza de nul. In exemplul de mai sus, barbatii si femeile nu difera semnificativ in privinta atitudinii fata de politica si politicieni.