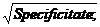|
|
|
Analiza factoriala
1. Problematica analizei factoriale
Cunoasterea complexului de factori in conexiunea lor are atat o importanta teoretica (vezi Big 5), cat si una practica (cunoscand realmente care sunt factorii, putem face o predictie valida in comportamentul uman).
Asa cum se stie, orice fenomen rezultativ, variabila dependenta, efect, s.a.m.d. poate fi determint de un numar mare de cauze.
Prin diferite strategii, se incearca izolarea unui numar redus de factori, lucru care s-a vazut in analiza de clusteri, in tabelul de asociere, in definirea legaturii de cauzalitate ne intereseaza nu numai cunoasterea factorilor, ci si sensul, intensitatea actiunii si marimea efectului, a partii ce revine actiunii fiecarui factor. De aceea, experimentul constituie metoda prin care putem izola cel mai bine factorii cauzali, ii putem manipula dupa cum dorim.
Dependenta statistica nu este intotdeauna echivalenta cu legatura cauzala, ci analiza logica a relatiei dintre variabile. O data admisa prezenta semnificativa a factorilor de influenta (VI), trebuie cuantificata contributia directa, cat si contributia interactiunii dintre factorii respectivi asupra variatiei VD.
De exemplu, am vazut acest lucru la dreapta de regresie.
Analiza factoriala a fost formulata in 1904 de Spearman pentru un model cu un singur factor comun si un factor specific (s). Thurstone, 1930, generalizeaza pentru un numar mai mare de factori.
Analiza factoriala are rolul de a arata ca un numar oricare de variabile dependete depind de o serie de factori nemasurati direct.
2. Principii ale analizei factoriale.Metode
Analiza factoriala este o metoda statistico-matematica de cercetare a relatiilor functionale ale unor rezultate.
Analiza factoriala cuprinde toate metodele de analiza si porneste de la intercorelatiile, covarianta unui ansamblu de variabile in functie de acesti factori.
Cunoscand relatiile ce exista intre testele unei baterii, analiza factoriala incearca sa izoleze si sa defineasca aptitudinile componente ale acestor teste, numite factori, precum si gradul de legatura dintre factor si testul respectiv.
Exista doua metode de analiza factoriala:
. metoda analizei componentelor principale (HOTTELING);
. metoda analizei centroide (THURSTONE)
Metoda analizei componentelor principale
Exemplu: presupunem ca am aplicat o baterie de 4 teste, iar intercorelatiile dintre ele se prezinta astfel:
![]()
Teste A B C D
![]()
A 1.00 0.200.26 0.31
B 1.00 0.16 0.17
C 1.00 0.22
D 1.00
Aceste date se introduc in calculator, obtinandu-se, in final, urmatorul tabel:
Teste Factorii componenti Suma patratelor
I II III IV
A 0.71 -0.30
B 0.56 0.82
C 0.64 -0.30
D 0.75 .
Suma patratelor 1.65 .
Proportii 0.41 0.22 0.21 0.16
Procente 41% 22% 21% 16% 100%
In spatele acestor teste aplicate exista 4 factori: primul fcator acopera 41% din varianta; daca factorul acopera 50% (unii spun 70%), atunci vorbim despre un factor general; daca nu - factor comun.
De asemenea, printr-un calcul specific se determina comunalitatea (cu cat contribuie factorul comun la test); coeficient de saturatie, valoarea de saturatie a unui test in factorul respectiv; se maicalculeaza specificitatea (ponderea atribuita unui anumit test); se calculeaza factorul specific.
Exemplu:
3 teste: - A = proba de desen;
B = proba verbala;
C = o proba de calcul numeric.
![]()
![]()
![]()
Teste Comunalitate Specificitate Factori specifici
![]() A 0.36 0.64 0.80
A 0.36 0.64 0.80
B 0.45 0.55 0.74
C 0.31 0.69 0.83
Specificitatea = 1- Comunalitatea;
Factorul specific =