
|
|
|
INFERENTA STATISTICA IN CAZUL DISTRIBUTIEI POISSON
Acest articol foloseste functiile de probabilitate si ML (maximum likelihooh), parametrul ce maximizeaza aceasta functie, pentru a realiza inferenta in cazul distributiilor de tip Poisson si Poisson multinomiala.
Presupunand ca avem date cu o distributie de tip Poisson, am aratat ca parametrul ce maximizeaza functia de probabilitate este chiar media si ca aceasta si varianta unei variabile aleatoare sunt aproximativ egale.
Pentru a testa ipoteza nula am folosit pe rand metoda Wald, metoda scorurilor si metoda likelihood-ratio si am determinat intervalul de incredere al parametrului pentru fiecare metoda prezentata.
De asemenea, am determinat estimatorii ML in cazul parametrilor Poisson multinomiali si am prezentat testul Pearson si testul G2, cel care foloseste likelihood-ratio.
Distributia Poisson
In cazul repartitiei binomiale, probabilitatea ca
un eveniment sa se verifice de y ori iar evenimentul contrar de n-y ori este ![]() unde y = 0, 1, 2,., n.
Cand n este moderat iar discrepanta dintre
unde y = 0, 1, 2,., n.
Cand n este moderat iar discrepanta dintre ![]() si
si ![]() este mare, atunci
distributia binomiala tinde spre cea poissoniana. Notam :
este mare, atunci
distributia binomiala tinde spre cea poissoniana. Notam :
![]() .
.
Pornind de la distributia binomiala, avem :
![]()
 .
.
Deoarece ![]() si
si 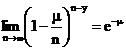 , avem:
, avem:
![]() unde
unde ![]() iar
iar ![]() este constanta.
Deoarece
este constanta.
Deoarece
![]() rezulta ca
rezulta ca ![]() este o functie
de frecventa.
este o functie
de frecventa.
Prin urmare, functia de distributie Poisson este ![]() unde y= 0,1 ,2 ,. iar
unde y= 0,1 ,2 ,. iar ![]() este parametrul de
distributie. Functia de distributie Poisson depinde de un unic parametru si
anume de
este parametrul de
distributie. Functia de distributie Poisson depinde de un unic parametru si
anume de ![]() care este chiar
numarul mediu de realizari ale evenimentului urmarit si care satisface conditia
care este chiar
numarul mediu de realizari ale evenimentului urmarit si care satisface conditia
![]() . Pentru
. Pentru ![]() si
si ![]() , functia de distributie Poisson este similara cu cea
binomiala. Cu cat
, functia de distributie Poisson este similara cu cea
binomiala. Cu cat ![]() creste, cu atat mai
mult distributia Poisson tinde spre normalitate.
creste, cu atat mai
mult distributia Poisson tinde spre normalitate.
Consideram functia generatoare a momentelor factoriale in cazul distributiei Poisson :
![]() .
.
Daca derivam functia ![]() succesiv, de h ori,
in raport cu t si apoi atribuim lui t valoarea 1, obtinem :
succesiv, de h ori,
in raport cu t si apoi atribuim lui t valoarea 1, obtinem :
![]() pentru h = 1, 2, 3, ..
Celelalte momente obisnuite si centrale se calculeaza cu ajutorul momentelor
factoriale. Se stie ca momentele
pentru h = 1, 2, 3, ..
Celelalte momente obisnuite si centrale se calculeaza cu ajutorul momentelor
factoriale. Se stie ca momentele ![]() sunt functii lineare
in raport cu numerele lui Stirling de speta a doua:
sunt functii lineare
in raport cu numerele lui Stirling de speta a doua: ![]()
Functia caracteristica a distributiei Poisson
este ![]() .
.
Introducem notiunea de abatere redusa ![]() cu
cu ![]() si consideram functia
caracteristica a acestei abateri :
si consideram functia
caracteristica a acestei abateri :

 . Obtinem
. Obtinem ![]() care este exact
functia caracteristica a legii normale cu dispersia 1. Frecventa asteptata ca
care este exact
functia caracteristica a legii normale cu dispersia 1. Frecventa asteptata ca ![]() este
este ![]() iar media este
iar media este ![]() unde
unde ![]() este numarul de evenimente
este numarul de evenimente
![]() . Varianta este data de relatia
. Varianta este data de relatia ![]() .
.
Distributia Poisson multinomiala
Consideram sirul de variabile aleatorii
independente X1, X2, .,Xn unde fiecare dintre
aceste variabile poate lua valorile a1, a2, ., am
cu probabilitatile respective ![]()
![]()
![]() iar
iar ![]() . Fiecare variabila
aleatoare Xi cu i= 1, 2, ., n da nastere unei distributii de forma :
. Fiecare variabila
aleatoare Xi cu i= 1, 2, ., n da nastere unei distributii de forma :
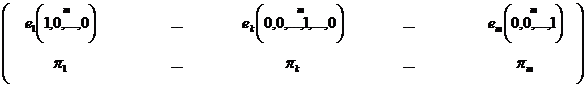
![]() unde vectorii
unde vectorii ![]() sunt liniar
independenti.
sunt liniar
independenti.
pozitia k
Notam ![]()
![]()
![]() unde
unde ![]()
![]()
![]() sunt niste
constante.
sunt niste
constante. ![]() este liniar
dependent de ceilalti
este liniar
dependent de ceilalti ![]() cu j = 1, 2, ., m-1. Probabilitatea
ca in n incercari successive vectorii
cu j = 1, 2, ., m-1. Probabilitatea
ca in n incercari successive vectorii ![]()
![]()
![]() sa apara respectiv de
sa apara respectiv de ![]() ori,
ori, ![]() ori, .,
ori, ., ![]() ori se comporta asimptotic dupa cum urmeaza:
ori se comporta asimptotic dupa cum urmeaza:
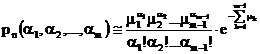 unde
unde ![]() .
.
Pornim de la distributia multinomiala pentru care avem relatia :
![]() .
.
Conform notatiilor
![]()
![]()
![]() ,
, ![]() obtinem:
obtinem:
![]()
Cum ![]() rezulta
rezulta ![]() deci
deci ![]() si obtinem
si obtinem
![]()
Stim ca ![]() deci
deci ![]() iar
cum
iar
cum ![]() obtinem
obtinem ![]()
Cunoscand faptul ca ![]() rezulta
rezulta 
Inlocuim rezultatul in relatia lui ![]() de mai sus si
obtinem:
de mai sus si
obtinem:
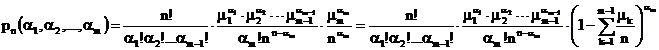
Pentru ![]() avem :
avem :
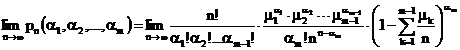 .
.
Tinand cont de faptul ca ![]() si
si  relatia de mai inainte devine:
relatia de mai inainte devine:
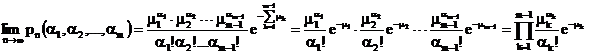 .
.
In concluzie, considerand distributia
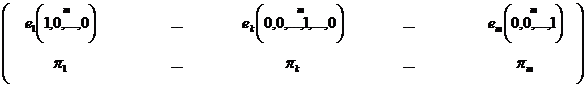
si avand relatia ![]() , probabilitatea ca, din n incercari, vectorii
, probabilitatea ca, din n incercari, vectorii
![]()
![]()
![]() sa apara respectiv de
sa apara respectiv de ![]() ori,
ori, ![]() ori, .,
ori, ., ![]() ori este:
ori este:
![]()
Prin definitie, functia caracteristica se va scrie :

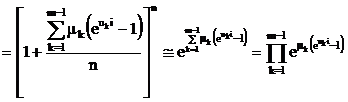 pentru valori
suficient de mari ale lui n.
pentru valori
suficient de mari ale lui n.
Introducem vectorul abaterilor reduse 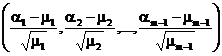 si scriem functia caracteristica :
si scriem functia caracteristica :
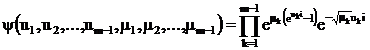 pentru valori suficient de mari ale lui n.
pentru valori suficient de mari ale lui n.
Trecand la limita obtinem:

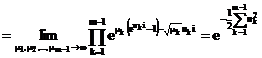 deoarece
deoarece ![]()
Deoarece functiile caracteristice ![]() tind catre functia
caracteristica a legii normale cu m-1 dimensiuni, rezulta ca si functiile de
repartitie corespunzatoare tind catre functia de repartitie a legii normale cu
m-1 dimensiuni.
tind catre functia
caracteristica a legii normale cu m-1 dimensiuni, rezulta ca si functiile de
repartitie corespunzatoare tind catre functia de repartitie a legii normale cu
m-1 dimensiuni.
Pentru determinarea momentelor unei distributii Poisson cu m-1 dimensiuni, plecam de la functia caracteristica a acestei distributii, a carei expresie este asimptotic egala cu
![]() deci,
deci,
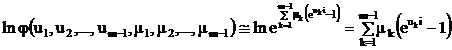
Observam faptul ca ![]() .
.
Inferenta statistica
Consideram un set de date pentru care avem probabilitatea de distributie si functia de probabilitate a acestor date pentru parametrul necunoscut. Se stie ca valoarea care maximizeaza functia de probabilitate maximizeaza si logaritmul acesteia.
Consideram parametrul ![]() iar estimatorul
valorii sale care maximeaza functia de probabilitate il notam cu
iar estimatorul
valorii sale care maximeaza functia de probabilitate il notam cu ![]() . Functia de
probabilitate a distributiei datelor o notam cu
. Functia de
probabilitate a distributiei datelor o notam cu ![]() iar logaritmarea acestei functii cu
iar logaritmarea acestei functii cu ![]() . Atunci,
. Atunci, ![]() este solutia ecuatiei
este solutia ecuatiei ![]() . Daca
. Daca ![]() este multidimensional,
atunci il notam cu
este multidimensional,
atunci il notam cu ![]() iar rezultatul sistemului
de ecuatii
iar rezultatul sistemului
de ecuatii ![]() cu
cu ![]() .
.
Inferenta statistica pentru parametrii Poisson
Consideram distributia data de functia
![]() . Coeficientul
. Coeficientul ![]() nu influenteaza valoarea
maxima a functiei
nu influenteaza valoarea
maxima a functiei ![]() . Prin urmare,
putem sa-l ignoram si sa folosim doar acea parte care implica parametrul
. Prin urmare,
putem sa-l ignoram si sa folosim doar acea parte care implica parametrul ![]() , parte numita nucleu.
, parte numita nucleu.
Avem ![]() si deci
si deci ![]()
Diferentiem in raport cu parametrul ![]() si obtinem
si obtinem ![]() . Atunci,
. Atunci,
![]() , adica numarul de evenimente realizate din cele n
incercari.
, adica numarul de evenimente realizate din cele n
incercari.
Daca diferentiem de doua ori in raport cu
parametrul ![]() , obtinem:
, obtinem:
![]() .
.
Consideram matricea al carei element de pe pozitia (i, j) are forma:
 unde
unde ![]()
Prin urmare, media si eroarea standard pentru ![]() au forma:
au forma:
![]() si respectiv
si respectiv 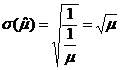
In concluzie, in cazul distributiei Poison media
si varianta unei variabile aleatoare sunt aproximativ egale ![]() .
.
In cele ce urmeaza determinam intervalul de
incredere al parametrului necunoscut pentru o caracteristica cu repartitie
Poisson cu legea de repartitie data de relatia ![]() Consideram
Consideram
![]() ca fiind numarul de evenimente
realizate din cele n incercari. Testam ipoteza nula
ca fiind numarul de evenimente
realizate din cele n incercari. Testam ipoteza nula ![]() . Pentru a
realiza inferenta statistica in cazul distributiei Poisson, vom folosi statistica
Wald
. Pentru a
realiza inferenta statistica in cazul distributiei Poisson, vom folosi statistica
Wald 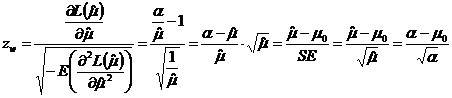
ce utilizeaza eroarea standard evaluata pentru ![]() sau statistica
scorurilor
sau statistica
scorurilor

in care eroarea standard este evaluata pentru ![]() . Pentru o eroare standard diferita de zero, statisticile
. Pentru o eroare standard diferita de zero, statisticile ![]() si
si ![]() au o distributie
apropiata de cea normala, in timp ce statisticile
au o distributie
apropiata de cea normala, in timp ce statisticile ![]() si
si ![]() au o distributie
au o distributie
![]() cu df=1.(Alan
Agrsti - 'Categorical Data Analysis' Second Edition, Wiley Interscience 2002)
cu df=1.(Alan
Agrsti - 'Categorical Data Analysis' Second Edition, Wiley Interscience 2002)
Logaritmul functiei de probabilitate in conditiile
ipotezei nule este ![]() iar, mai general, pentru
iar, mai general, pentru
![]() , este
, este ![]() . Notam
. Notam ![]() . Atunci,
testul statistic numit probabilitatea ratiilor (likelihood-ratio statistic)
este dat de relatia:
. Atunci,
testul statistic numit probabilitatea ratiilor (likelihood-ratio statistic)
este dat de relatia:

si, asa cum a aratat Wilks (1935,1938), are o
distributie ![]() pentru
pentru ![]() . Cum sub ipoteza
nula nu avem nici un parametru iar sub ipoteza alternativa avem un unic
parametru, rezulta ca avem un unic grad de libertate.
. Cum sub ipoteza
nula nu avem nici un parametru iar sub ipoteza alternativa avem un unic
parametru, rezulta ca avem un unic grad de libertate.
Pentru determinarea intervalului de incredere
pornim de la statistica Wald si spunem ca intervalul de incredere al valorilor pe
care le poate lua ![]() este dat de
relatia
este dat de
relatia ![]() sau de
sau de  , adica
, adica ![]() . Pentru statistica scorurilor avem intervalul de
incredere
. Pentru statistica scorurilor avem intervalul de
incredere ![]() sau
sau 
Daca folosim probabilitatea ratiilor
(likelihood-ratio statistic) adica 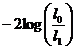 care are o
distributie
care are o
distributie ![]() pentru
pentru ![]() , atunci se considera a fi interval de incredere
intervalul pentru care obtinem o valoare mai mica decat
, atunci se considera a fi interval de incredere
intervalul pentru care obtinem o valoare mai mica decat ![]() pentru
pentru ![]() unde
unde ![]() este numarul de evenimente
realizate din n incercari. Daca statistica Wald si statistica ce foloseste
probabilitatea ratiilor ne ofera rezultate ce difera foarte mult, acest lucru
sugereaza faptul ca
este numarul de evenimente
realizate din n incercari. Daca statistica Wald si statistica ce foloseste
probabilitatea ratiilor ne ofera rezultate ce difera foarte mult, acest lucru
sugereaza faptul ca ![]() are o
distributie ce deviaza mult de la normalitate. Atunci cand
are o
distributie ce deviaza mult de la normalitate. Atunci cand ![]() are o distributie normala, functia
are o distributie normala, functia ![]() are o reprezentare grafica parabolica. In cazul
esantioanelor de volum redus ce contin date categoricale,
are o reprezentare grafica parabolica. In cazul
esantioanelor de volum redus ce contin date categoricale, ![]() deviaza mult de
la normalitate iar functia
deviaza mult de
la normalitate iar functia ![]() nu va mai avea o
reprezentare grafica simetrica si parabolica. Acest lucru se poate intampla si
in cazul esantioanelor de volum moderat sau mare care au multi parametri. In toate aceste situatii este preferabil sa
determinam intervalul de incredere bazat pe probabilitatea ratiilor. (Alan
Agrsti - 'Categorical Data Analysis' Second Edition, Wiley Interscience 2002)
nu va mai avea o
reprezentare grafica simetrica si parabolica. Acest lucru se poate intampla si
in cazul esantioanelor de volum moderat sau mare care au multi parametri. In toate aceste situatii este preferabil sa
determinam intervalul de incredere bazat pe probabilitatea ratiilor. (Alan
Agrsti - 'Categorical Data Analysis' Second Edition, Wiley Interscience 2002)
Inferenta statistica pentru parametrii Poisson multinomiali
Consideram sirul de variabile aleatorii independente
X1, X2, .,Xn unde fiecare dintre aceste
variabile poate lua valorile a1, a2, ., am cu
probabilitatile respective ![]()
![]()
![]() unde
unde ![]() . Asa cum am prezentat
intr-un paragraf anterior, fiecare variabila aleatoare Xi cu i= 1, 2, ., n da nastere unei distributii de forma :
. Asa cum am prezentat
intr-un paragraf anterior, fiecare variabila aleatoare Xi cu i= 1, 2, ., n da nastere unei distributii de forma :
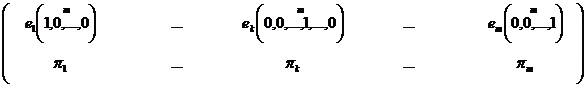
![]() vectorii
vectorii ![]() fiind liniar
independenti.
fiind liniar
independenti.
pozitia k
Notam ![]()
![]()
![]() unde
unde ![]()
![]()
![]() sunt niste
constante iar
sunt niste
constante iar ![]() este liniar
dependent de ceilalti
este liniar
dependent de ceilalti ![]() cu j = 1, 2, .,
m-1.
cu j = 1, 2, .,
m-1.
Probabilitatea ca in n incercari successive
vectorii ![]()
![]()
![]() sa apara respectiv de
sa apara respectiv de ![]() ori,
ori, ![]() ori, .,
ori, ., ![]() ori se comporta asimptotic dupa cum urmeaza:
ori se comporta asimptotic dupa cum urmeaza:
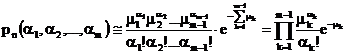
unde ![]() si
si ![]() iar
iar ![]() i=1,.,m. Valorile
i=1,.,m. Valorile
![]() au o distributie
Poisson multinomiala iar
au o distributie
Poisson multinomiala iar ![]() este functia de
distributie Poisson multinomiala. Deoarece
este functia de
distributie Poisson multinomiala. Deoarece ![]() rezulta ca
rezulta ca ![]()
Coeficientul ![]() nu influenteaza
valoarea ce maximizeaza functia de distributie si, prin urmare, putem sa-l
ignoram.
nu influenteaza
valoarea ce maximizeaza functia de distributie si, prin urmare, putem sa-l
ignoram.
Obtinem :
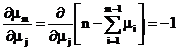
si
![]()
Probabilitatea maxima (ML) este acea probabilitate
ce maximizeaza logaritmul expresiei ![]()
![]()
Diferentiem ![]() in raport cu
in raport cu ![]() si obtinem ecuatia de
probabilitate (likelihood equation) :
si obtinem ecuatia de
probabilitate (likelihood equation) :
![]()
![]() .
.
Cum ![]() , obtinem solutia ce
maximizeaza probabilitatea astfel:
, obtinem solutia ce
maximizeaza probabilitatea astfel:
![]() si
si ![]()
Un prim test folosit in cazul distributiei Poisson
multinomiala este testul Pearson. Consideram ipoteza nula ![]() j=1, 2,.,m unde
j=1, 2,.,m unde ![]() sau altfel spus,
sau altfel spus, ![]() j=1,2,..,m unde
j=1,2,..,m unde ![]() . Cand ipoteza nula este adevarata, frecventele teoretice
sunt
. Cand ipoteza nula este adevarata, frecventele teoretice
sunt ![]() j=1,.,m iar frecventele observate sunt
j=1,.,m iar frecventele observate sunt ![]() j= 1, 2, ., m.
j= 1, 2, ., m.
Statistica ![]() a lui Pearson
a lui Pearson 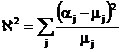 are urmatoarele
proprietati:
are urmatoarele
proprietati:
![]()
Cand frecventele observate sunt egale cu
frecventele teoretice, adica ![]() pentru toate perechile,
atunci
pentru toate perechile,
atunci ![]() .
.
Daca diferentele dintre frecventele observate si
frecventele teoretice ![]() sunt mari atunci
si valorile lui
sunt mari atunci
si valorile lui ![]() vor fi mari.
vor fi mari.
Ipoteza diferentei nule este acceptata cu o probabilitate
de 95% daca ![]()
Pentru esantioanele mari, statistica ![]() are o distributie
aproximativ chi-patrat cu df=m-1.
are o distributie
aproximativ chi-patrat cu df=m-1.
Un alt test utilizat in cazul distributiei Poisson multinomiale este
testul ![]() , cel care foloseste ratia probabilitatilor. Asa cum am
aratat mai sus, functia de probabilitate a distributiei Poisson multinomiala
este maximizata cand
, cel care foloseste ratia probabilitatilor. Asa cum am
aratat mai sus, functia de probabilitate a distributiei Poisson multinomiala
este maximizata cand ![]() si
si ![]() . Atunci, probabilitatea ratiilor (likelihood-ratio
statistic) va avea forma:
. Atunci, probabilitatea ratiilor (likelihood-ratio
statistic) va avea forma:

iar

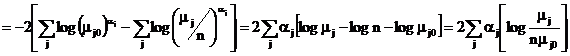
Deci 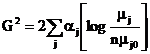 iar df=m-1.
iar df=m-1.
Observatie : Cu cat n este mai mare, cu atat ![]() are o distributie mai apropiata de distributia
are o distributie mai apropiata de distributia ![]() cu m-1 grade de libertate. Cu cat
cu m-1 grade de libertate. Cu cat ![]() are valori mai mari, cu atat exista mai multe argumente
impotriva ipotezei nule. (Alan Agrsti - 'Categorical Data Analysis' Second
Edition, Wiley Interscience 2002)
are valori mai mari, cu atat exista mai multe argumente
impotriva ipotezei nule. (Alan Agrsti - 'Categorical Data Analysis' Second
Edition, Wiley Interscience 2002)
Bibliografie
1. Alan Agrsti - 'Categorical Data Analysis' Second Edition, Wiley Interscience, New Jersey 2002
2. Carolyn. J. Anderson - 'Applied Categorical Data Analysis', EdPsych 590AT/Psych 593, 2006
3. Ronald N. Forthofer, Eun Sul Lee, Michael Hernandez - 'Biostatistics - A Guide to Design, Analysis, and Discovery' Second Edition, Elsevier, 2007
4. Harold A. Kahn, Cristopher
T. Sempos - 'Statistical Methods in Epidemiology',
5. Dumitru Sandu - 'Statistica in stiintele sociale - Probleme teoretice si aplicatii pentru invatamantul universitar', Universitatea Bucuresti, Facultatea de Sociologie, Psihologie si Pedagogie, 1992
6. Ilie P. Vasilescu - 'Statistica informatizata pentru stiinte despre om', Editura Militara, Bucuresti, 1992