|
|
|
TESTAREA IPOTEZELOR DESPRE O SINGURA POPULATIE
In acest capitol sunt expuse tehnici statistice de testare a ipotezelor despre o singura populatie. Intr-un astfel de caz, pe baza unei statistici calculate pentru un esantion, cel mai adesea o medie aritmetica sau o proportie, se trage o concluzie despre parametrul corespunzator al populatiei de referinta. Mai precis, cercetarea consta din alcatuirea unui esantion aleatoriu din populatia de referinta, culegerea informatiei relevante din esantion, calcularea valorii unei statistici si compararea acestei valori cu valoarea presupusa a parametrului corespunzator. In aproape toate situatiile de cercetare vom gasi o anumita diferenta intre cele doua valori, iar tehnicile de testare a ipotezelor permit sa se decida daca diferenta este atat de mare, incat sa justifice respingerea presupunerii facute pentru populatie.
Tehnicile de testare a ipotezelor prezentate in acest capitol si in capitolele care urmeaza sunt teste despre valoarea parametrilor unei populatii si cer indeplinirea unor conditii sau supozitii despre populatiile respective, cum este, in principal, normalitatea. Testele de acest fel se numesc teste parametrice.
1 TESTUL SCORURILOR Z PENTRU MEDII ARITMETICE
CAND σ ESTE CUNOSCUT
Vom prezenta acest test cu ajutorul unui exemplu, pe care il vom folosi si pentru a introduce notiunile fundamentale ale testelor parametrice: ipoteza de nul, ipoteza alternativa, statistica a testului si regula de decizie.
Un cercetator presupune ca intr-un anumit an, media aritmetica a punctajelor obtinute la examenul de rezidentiat al medicilor este de 800. Pentru a testa aceasta ipoteza, cercetatorul alcatuieste un esantion aleatoriu de 130 de medici care si-au sustinut rezidentiatul in acel an si constata ca la nivelul acestui esantion media aritmetica a punctajului obtinut este de 755. Prin investigatii extensive, cercetatorul stie ca abaterea standard la nivelul populatiei de referinta este de aproximativ 152. Problema care se pune este daca diferenta dintre media aritmetica a esantionului si valoarea presupusa pentru populatie este sau nu statistic semnificativa. Daca raspunsul este afirmativ, atunci ipoteza facuta poate fi respinsa. Daca, insa, raspunsul este negativ, atunci diferenta poate fi pusa pe seama intamplarii, astfel ca ipoteza cercetatorului nu poate fi respinsa. Dupa cum vom vedea, testul scorurilor Z permite determinarea matematica a intelesului termenului "statistic semnificativ". Datele problemei sunt, deci, urmatoarele:
Populatie
Esantion
μH = 800
σ = 152
n = 130
Am notat cu μH media aritmetica presupusa a populatiei, pentru a o deosebi de media aritmetica efectiva a populatiei, μ.
Ipoteza de nul, pe care o vom nota H0, specifica o anumita valoare pentru parametrul respectiv. In general, ipoteza de nul despre media aritmetica a unei populatii are forma
H0: μ = μH
Denumirea de "ipoteza de nul" se justifica prin aceea ca forma sa poate fi redata echivalent prin
H0: μ μH = 0
In cuvinte, ipoteza de nul enunta ca nu exista nici o diferenta semnificativa intre valoarea efectiva a parametrului respectiv si valoarea presupusa a acelui parametru. Daca ipoteza de nul este adevarata, atunci diferenta dintre esantion si populatie nu este semnificativa, putand fi atribuita intamplarii.
In mod obisnuit, cercetatorul este de parere ca exista o diferenta semnificativa intre esantion si populatie si doreste sa respinga ipoteza de nul ca neadevarata. Aceasta opinie constituie ipoteza alternativa, pe care o vom nota cu Ha. Daca cercetatorul nu are posibilitatea sau nu doreste sa prezica sensul diferentei, atunci ipoteza alternativa ia forma
Ha: μ μH
Daca, insa, sensul diferentei dintre esantion si populatie poate fi prezis sau daca cercetatorul este interesat doar de un singur sens al diferentei, atunci ipoteza alternativa poate lua una dintre urmatoarele doua forme:
Ha: μ > μH
Ha: μ < μH
In cazul in care Ha are forma μ μH, se spune ca testul este bilateral sau non-directional, iar in cazurile in care Ha are una dintre celelalte doua forme, se spune ca testul este unilateral sau directional. Vom reveni la aceste notiuni ceva mai departe. Sa retinem deocamdata ca in orice test se decide daca se respinge sau nu se respinge ipoteza de nul, pe baza dovezilor aduse in sprijinul ipotezei alternative. Astfel, daca putem respinge H0 ca neadevarata, atunci vom accepta Ha.
Revenind la exemplul nostru, ipoteza de nul este H0: μ = 800. Din enuntul problemei rezulta ca nu este vorba despre un sens al diferentei mentionate, astfel ca ipoteza alternativa este Ha: μ 800.
Termenul statistica a testului se refera la formula a carei aplicare in testul respectiv permite obtinerea unei valori ce formeaza baza deciziei asupra ipotezei de nul. Pentru mediile aritmetice, atunci cand se cunoaste sau se poate aproxima valoarea lui σ, statistica testului este data de urmatoarea formula:
Formula 1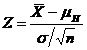 
Sa notam ca
aceasta formula este analoaga structural formulelor de calcul
pentru transformarea unui scor "brut" X in scorul Z
corespunzator (v. sectiunea 4.2), aici fiind vorba despre scorul Z
al unei medii aritmetice. Ca atare, in numitorul formulei 1 apare abaterea
standard a distributiei de esantionare a 
, astfel ca aceasta formula ne da
distanta in abateri standard sau fractiuni de abateri standard a
mediei aritmetice a esantionului, , fata de valoarea presupusa pentru
populatie. In exemplul nostru, avem
Din motive care vor deveni imediat evidente, vom desemna rezultatul aplicarii formulei 1 prin Z (obtinut). Aici, Z (obtinut) = 3,36.
Regula
de decizie se refera la o anumita amplitudine de valori pentru
rezultatul statisticii testului, numita zona critica sau zona
de respingere, care conduce la respingerea ipotezei de nul. In cazul
testului scorurilor Z pentru medii aritmetice, zona critica se
stabileste cu ajutorul distributiei de esantionare a . Astfel, in exemplul de mai sus, esantionul
alcatuit este unul dintre toate esantioanele posibile cu n =
130 din populatia de referinta. Sa presupunem ca H0
este adevarata, Daca s-ar calcula toate mediile aritmetice
posibile, atunci teorema limitei centrale asigura urmatorul rezultat:
755 μ = 800 
In general, cu cat este mai aproape de
centru (diferenta dintre si 
este mai mica),
cu atat vom fi mai inclinati sa nu respingem ipoteza de nul si
cu cat este mai departe de
centru (diferenta dintre si este mai mare), cu
atat vom fi mai inclinati sa respingem ipoteza de nul. Cu alte
cuvinte, ipoteza de nul poate fi respinsa daca rezultatul statisticii
testului este un numar negativ "prea mare" sau un numar pozitiv "prea
mare". Intelesul expresiei "prea mare" se fixeaza prin alegerea unui
nivel de incredere sau nivel α (revedeti capitolul anterior).
In cazul ipotezei alternative de forma Ha: μ μH, nivelul α
ales se imparte in mod egal in cele doua extremitati ale
distributiei de esantionare:
α/2 α/2
Zα/2
Zα/2
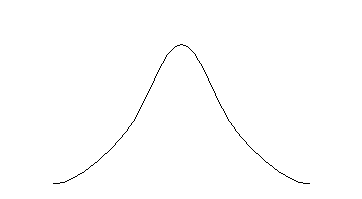
Aria de sub Zα/2 plus aria de peste +Zα/2 reprezinta zona critica: daca scorul Z corespunzator mediei aritmetice a unui esantion cade in aceasta arie (i.e. sub Zα/2 sau peste +Zα/2), atunci media aritmetica respectiva are prin definitie o probabilitate de aparitie mai mica decat α. Scorurile Zα/2 si +Zα/2 se numesc scoruri Z critice si se desemneaza, respectiv, prin Zα/2 (critic) si +Zα/2 (critic).
Sa revenim iarasi la exemplul nostru si sa stabilim α = 0,05. Stim ca pentru aceasta valoare a lui α, Zα/2 = 1,96. Z (obtinut) se afla in zona critica ( 3,36 < 1,96), dupa cum se ilustreaza in figura urmatoare:
1,96
1,96
|
-3,36
Ca atare, suntem indreptatiti sa respingem ipoteza de nul: probabilitatea de aparitie a mediei aritmetice a esantionului considerat este mai mica decat 0,05 si deci nu poate fi atribuita intamplarii. Cu alte cuvinte, diferenta dintre media aritmetica a esantionului si media aritmetica presupusa pentru populatie este statistic semnificativa (esantionul de rezidenti difera semnificativ de populatia din care a fost selectat), astfel ca ipoteza de nul poate fi respinsa.
De notat ca decizia pe care am luat-o (respingerea ipotezei de nul) comporta un element de risc: aceasta decizie poate fi gresita, intrucat este posibil ca esantionul considerat sa fie unul dintre putinele esantioane nereprezentative pentru populatia de medici rezidenti. O trasatura foarte importanta a testarii ipotezelor consta din aceea ca probabilitatea de a lua o decizie gresita este cunoscuta, fiind data de nivelul α ales. In exemplul nostru, probabilitatea de a lua o decizie gresita este de 0,05. A spune ca probabilitatea de a fi respins gresit ipoteza de nul este de 0,05 revine la a spune ca daca am repeta acest test de o infinitate de ori, vom respinge gresit H0 doar de 5 ori la fiecare 100 de repetari. Rezultatul de mai sus poate fi enuntat si spunand ca diferenta mentionata este statistic semnificativa la un nivel de incredere de 95%. Ca si pentru estimarea intervalelor, nivelurile de incredere folosite in mod obisnuit in testarea ipotezelor sunt 90%, 95% si 99%.
Testul intreprins in acest exemplu este bilateral sau nedirectional. In general, intr-un astfel de test, ipoteza alternativa enunta doar ca exista o diferenta intre valoarea efectiva a parametrului respectiv si valoarea presupusa pentru acel parametru. Dupa cum am vazut, in cazul unui test bilateral, zona critica specificata de nivelul α se imparte in mod egal in cele doua extremitati ale distributiei de esantionare. Intr-un test bilateral, indiferent de nivelul α ales, regula de decizie este urmatoarea:
Se respinge H0, daca Z (obtinut) > +Zα/2 (critic) sau daca Z (obtinut) < Zα/2 (critic)
Intr-un test unilateral sau directional, daca cercetatorul crede ca valoarea efectiva a parametrului este mai mare decat valoarea presupusa, Ha ia forma μ > μH, iar pentru un test in sensul opus, Ha ia forma μ < μH.. In cazul unui test unilateral, intreaga zona critica specificata de nivelul α este plasata in extremitatea de interes a distributiei de esantionare. De pilda, intr-un test bilateral in care α = 0,05, zona critica incepe de la Zα/2 (critic) = 1,96. Intr-un test unilateral, la acelasi nivel α, Zα (critic) este +1,65 daca este vorba despre extremitatea superioara (daca Ha este de forma μ > μH) si este 1,65 daca este vorba despre extremitatea inferioara (daca Ha este de forma μ < μH)[1]. De notat ca aici folosim Zα in loc de Zα/2, intrucat intreaga zona critica este plasata intr-o singura extremitate a distributiei de esantionare.
Intr-un test unilateral, indiferent de nivelul α ales, daca Ha este de forma μ > μH ("test unilateral dreapta"), atunci regula de decizie este
Se respinge H0, daca Z (obtinut) > +Zα (critic)
Daca Ha este de forma μ < μH ("test unilateral stanga") atunci regula de decizie este
Se respinge H0, daca Z (obtinut) < Zα (critic)
Dupa cum rezulta si din cele de mai sus, un test unilateral este mai "bun" decat unul bilateral, deoarece zona critica este "trasa" mai aproape de media aritmetica, imbunatatind astfel probabilitatea de a respinge H0. Astfel, daca cercetatorul are mai multa experienta si mai multe cunostinte in legatura cu variabila investigata, atunci se recomanda folosirea unui test unilateral, ceea ce cere o ipoteza alternativa directionala.
Se obisnuieste ca testarea ipotezelor statistice sa fie organizata sub forma unui "model in n pasi", numarul de pasi diferind de la un autor la altul in functie de anumite optiuni de compactare sau de detaliere a informatiei. In cele ce urmeaza vom folosi un model in 4 pasi, pe care il exemplificam pentru problema tratata mai sus:
H0: μ = 800
Ha: μ 800
Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice
Distributia de esantionare = Distributia Z
α = 0,05 (test bilateral)
Zα/2 (critic) = 1,96
(Zona critica este notata prin scorurile Z care ii marcheaza inceputurile).
Pasul 3. Calcularea statisticii testului
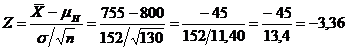
Pasul 4. Luarea deciziei
Intrucat Z (obtinut) se afla in zona critica ( 3,36 < 1,96), ipoteza de nul poate fi respinsa. Diferenta dintre esantionul de medici rezidenti si populatia de referinta nu poate fi atribuita intamplarii sau, altfel spus, aceasta diferenta este statistic semnificativa (la un nivel de incredere de 95%).
Pentru a ilustra aplicarea unui test unilateral, sa presupunem ca cercetatorul din exemplul de mai sus doreste sa testeze ipoteza ca media aritmetica a populatiei de rezidenti este mai mica decat 800, toate celelalte date fiind aceleasi. In acest caz, cercetatorul este interesat doar de extremitatea stanga a distributiei de esantionare si va plasa intreaga zona critica in aceasta extremitate. In termenii modelului in patru pasi, testul decurge dupa cum urmeaza:
H0: μ = 800
Ha: μ < 800
Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice
Distributia de esantionare = Distributia Z
α = 0,05 (test unilateral stanga)
Zα (critic) = 1,65
Pasul 3. Calcularea statisticii testului
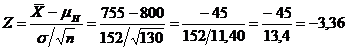
Pasul 4. Luarea deciziei
Intrucat Z (obtinut) se afla in zona critica ( 3,36 < 1,65), ipoteza de nul poate fi respinsa si se poate accepta ca media aritmetica a populatiei de rezidenti este mai mica decat 800 (la un nivel de incredere de 95%).
2 ERORI IN TESTAREA IPOTEZELOR
Atunci cand decidem sa respingem sau sa nu respingem ipoteza de nul, sunt posibile patru situatii, descrise in figura urmatoare:
H0 adevarata
H0 falsa
Se respinge H0
Eroare de
tipul I
Decizie corecta
Nu se respinge H0
Decizie corecta
Eroare de
tipul II
Dupa cum se indica in figura 1, H0 este in realitate adevarata sau falsa si sunt posibile doua decizii: se respinge H0 sau nu se respinge H0. Ca atare, sunt posibile doua decizii corecte: respingerea unei ipoteze de nul false si nerespingerea unei ipoteze de nul adevarate. Corespunzator, sunt posibile doua decizii gresite: respingerea unei ipoteze ne nul care este adevarata, numita eroare de tipul I, si nerespingerea unei ipoteze de nul care este falsa, numita eroare de tipul II. Probabilitatea de a comite o eroare de tipul I este desemnata prin α, iar probabilitatea de a comite o eroare de tipul II este desemnata prin β.
Probabilitatea de a comite o eroare de tipul I este determinata de nivelul α ales. Astfel, atunci cand se alege un nivel α, distributia de esantionare este impartita in doua multimi de rezultate ale esantioanelor posibile: zona critica, ce include toate rezultatele definite ca improbabile sau rare si care indreptatesc respingerea H0, si zona necritica, ce consta din toate rezultatele definite drept "non-rare". Cu cat nivelul α este mai mic, cu atat este mai mica zona critica si, corespunzator, este mai mare distanta dintre media aritmetica a distributiei de esantionare si inceputurile (in cazul unui test bilateral) sau inceputul (in cazul unui test unilateral) zonei critice. De pilda, daca se alege α = 0,05, probabilitatea de a comite o eroare de tipul I este de 0,05: daca H0 este respinsa, exista 5 sanse din 100 ca aceasta decizie sa fie gresita; daca α = 0,01, probabilitatea de a comite o eroare de tipul I este de 0,01: daca H0 este respinsa, exista doar 1 sansa din 100 ca aceasta decizie sa fie gresita. Prin urmare, pentru a minimiza probabilitatea de a comite o eroare de tipul I, trebuie sa folosim nivele α foarte mici.
Pe de alta parte, cu cat nivelul α este mai mic, cu atat este mai mare zona necritica si, pastrand celelalte date constante, este mai putin probabil ca rezultatul obtinut pe esantion sa cada in zona critica, deci este mai mare probabilitatea de a comite o eroare de tipul II.
Prin urmare, cele doua probabilitati sunt invers proportionale, nefiind posibil sa le minimizam pe amandoua: daca alegem un nivel α foarte mic pentru a pentru a minimiza probabilitatea de a comite o eroare de tipul I, creste probabilitatea de a comite o eroare de tipul II. Cu alte cuvinte, daca crestem dificultatea de a respinge ipoteza de nul, probabilitatea de a nu respinge ipoteza de nul atunci cand aceasta este falsa creste. In mod normal, in stiintele omului se doreste minimizarea probabilitatii erorii de tipul I, socotita a fi mai grava decat eroarea de tipul II, astfel ca se aleg valori mici pentru α.
In tabelul urmator sunt prezentate cateva scoruri Z critice pentru nivele α mai des folosite, atat pentru teste bilaterale, cat si pentru teste unilaterale:
Niveluri α
test bilateral
test unilateral
De regula, nivelul α = 0,05 este considerat drept un indicator bun al unui rezultat semnificativ.
3 TESTAREA IPOTEZELOR PENTRU MEDII ARITMETICE
Ca si in privinta estimarii intervalelor, in aproape toate situatiile reale de cercetare, valoarea abaterii standard a populatiei este necunoscuta. Si aici vom distinge doua cazuri: cazul in care dimensiunea esantionului este mare, ceea ce inseamna esantioane cu n > 30, si cazul n 30. In cazul esantioanelor cu n > 30, σ se poate estima prin s, iar in pasul 3 se foloseste urmatoarea formula:
Formula 2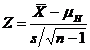 
Aceasta formula difera de formula 1 prin aceea ca σ este inlocuit cu s, iar n este inlocuit cu n - 1 pentru a se corecta distorsiunea lui s.
In cazul esantioanelor cu n 30, distributia de esantionare este distributia t Student, prezentata in capitolul 6, iar in pasul 3 se foloseste urmatoarea formula:
Formula 3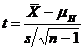 
Vom spune ca este vorba despre testul scorurilor t pentru medii aritmetice si vom desemna rezultatul aplicarii formulei 3 prin t (obtinut).
Sa presupunem ca un cercetator primeste informatia neverificata conform careia media aritmetica a coeficientului de inteligenta al participantilor la fazele nationale ale olimpiadelor de matematica din ultimii 10 ani este de aproximativ 125. Pentru a testa aceasta ipoteza, cercetatorul selecteaza un esantion aleatoriu de 20 de olimpici la matematica din ultimii 10 ani si constata ca media aritmetica a coeficientului de inteligenta la nivelul esantionului este de 123, abaterea standard la nivelul esantionului fiind de 8. Cercetatorul este interesat sa determine la un nivel de incredere de 99% daca media aritmetica a coeficientului de inteligenta al participantilor la fazele nationale ale olimpiadelor de matematica din ultimii 10 ani este mai mare de 125. Datele problemei sunt, deci, urmatoarele:
Populatie
Esantion
μH = 125
s = 8
n = 20
H0: μ = 125
Ha: μ > 125
Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice
Distributia de esantionare = Distributia t
α = 0,01 (test unilateral dreapta)
gl = 20 1 = 19
tα (critic) = +2,539
Pasul 3. Calcularea statisticii testului
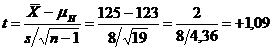
Pasul 4. Luarea deciziei
Intrucat t (obtinut) nu cade in zona critica (+1,09 < +2,539), cercetatorul nu poate respinge ipoteza de nul. Pe baza mediei aritmetice a esantionului nu se poate conchide la un nivel de incredere de 99% ca media aritmetica a coeficientului de inteligenta al participantilor la fazele nationale ale olimpiadelor de matematica din ultimii 10 ani este mai mare de 125. Rezultatul acestui test este prezentat grafic in figura urmatoare:
+2,539 0
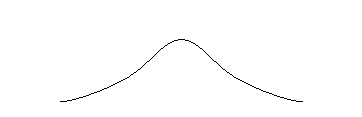
+1,09
In cazul folosirii distributiei t ca distributie de esantionare, regulile de decizie au aceeasi structura cu cele ale testului scorurilor Z. Astfel, intr-un test bilateral, indiferent de nivelul α ales si de numarul de grade de libertate, regula de decizie este urmatoarea:
Se respinge H0, daca t (obtinut) > +tα/2 (critic) sau daca t (obtinut) < tα/2 (critic)
Intr-un test unilateral dreapta (μ > μH), regula de decizie este
Se respinge H0, daca t (obtinut) > +tα (critic)
In fine, intr-un test unilateral stanga (μ < μH), regula de decizie este
Se respinge H0, daca t (obtinut) < tα (critic)
4 TESTUL SCORURILOR Z PENTRU PROPORTII
Atunci cand variabila de interes nu este de interval sau de raport, astfel incat sa se justifice calcularea mediei aritmetice, se poate utiliza proportia esantionului (p) in loc de media aritmetica. In cele ce urmeaza, prezentam un test al ipotezelor pentru proportii, aplicabil in cazul esantioanelor pentru care np 5 si n(1 p) 5.
In acest test,
formula de calcul pentru Z (obtinut) are aceeasi
structura cu formula 1: Z (obtinut) este egal cu marimea
pentru esantion minus valoarea presupusa pentru parametrul
corespunzator, totul de impartit la abaterea standard a
distributiei de esantionare. Din capitolul anterior, stim
ca proportiile pentru esantioane (p) au distributii
de esantionare aproximativ normale, cu media aritmetica (μp)
egala cu proportia pentru populatie (P) si abaterea
standard (σp) egala cu 
. Teoretic, formula de calcul al testului scorurilor Z
pentru proportii este urmatoarea:
Formula 4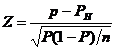 
unde PH este proportia presupusa pentru populatie. Acum, valoarea proportiei pentru populatie, P, nu este cunoscuta. Ca si in cazul estimarii intervalelor pentru proportii, putem estima valoarea lui P prin p, lucrand cu formula urmatoare:
Formula 5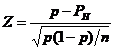 
Sa consideram un exemplu. Se pretinde ca aproximativ 10% din studentii unei mari universitati sunt casatoriti. Pentru testarea acestei ipoteze, se selecteaza un esantion aleatoriu de 200 de studenti de la universitatea respectiva si se constata ca 24 de studenti din esantion sunt casatoriti. In baza acestui rezultat, se poate spune la un nivel de incredere de 95% ca mai mult de 10% din studenti sunt necasatoriti? Datele problemei sunt urmatoarele:
Populatie
Esantion
PH = 0,10
p = 0,12
n = 200
Folosind formula 5, testul decurge dupa cum urmeaza:
H0: P = 0,10
Ha: P > 0,10
Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice
Distributia de esantionare = Distributia Z
α = 0,05 (test unilateral dreapta)
Zα (critic) = +1,65
Pasul 3. Calcularea statisticii testului
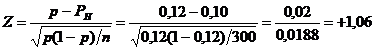
Pasul 4. Luarea deciziei
Intrucat Z (obtinut) nu cade in zona critica (+1,06 < +1,65), ipoteza de nul nu poate fi respinsa. La nivelul de incredere de 95% nu se poate spune ca mai mult de 10% din studenti sunt necasatoriti.
GLOSAR
Eroare de tipul I: respingerea unei ipoteze de nul care este adevarata; probabilitatea de a comite o eroare de tipul I este desemnata prin α.
Eroare de tipul II: nerespingerea unei ipoteze de nul care este falsa; probabilitatea de a comite o eroare de tipul II este desemnata prin β.
Ipoteza alternativa: in contextul statisticilor inferentiale, ipoteza care enunta ca exista o diferenta intre valoarea efectiva a unui parametru si valoarea presupusa pentru acel parametru; daca sensul diferentei poate fi prezis, ipoteza alternativa este directionala, in caz contrar este nedirectionala.
Ipoteza de nul: in contextul statisticilor inferentiale, ipoteza care enunta nu exista nici o diferenta semnificativa intre valoarea efectiva a unui parametru si valoarea presupusa a acelui parametru.
Regula de decizie: enunt referitor la o anumita amplitudine de valori pentru rezultatul statisticii testului, numita zona critica sau zona de respingere, care conduce la respingerea ipotezei de nul.
Statistica a testului: formula a carei aplicare in testul respectiv permite obtinerea unei valori ce formeaza baza deciziei asupra ipotezei de nul.
Teste parametrice: teste statistice despre valoarea parametrilor unei populatii, care cer indeplinirea unor conditii sau supozitii despre populatiile respective, cum este, in principal, normalitatea.
Test bilateral: test statistic in care ipoteza alernativa este non-directionala.
Test unilateral: test statistic in care ipoteza alternativa este directionala.
[1] Scadem 0,05 din 0,5 (proportia de cazuri aflate de o parte si de alta a mediei aritmetice a distributiei de esantionare). Rezultatul scaderii este 0,4500. Conform tabelului distributiei normale standard, scorul Z corespunzator acestei proportii este 1,65.
