Estimarea mediei aritmetice cand σ este necunoscut. distributia t-student

ESTIMAREA MEDIEI ARITMETICE CAND σ ESTE NECUNOSCUT. DISTRIBUTIA t-STUDENT

In aproape toate situatiile reale de cercetare, valoarea abaterii standard a populatiei este necunoscuta. Se disting aici doua cazuri: cazul in care dimensiunea esantionului este relativ mare, ceea ce inseamna esantioane cu n > 30, si cazul n 30.

In cazul esantioanelor cu n > 30, σ se poate estima prin s (abaterea standard a esantionului). Intrucat, dupa cum am vazut, s este un estimator distorsionat pentru σ, formula de construire a intervalului de incredere estimat este usor modificata fata de formula 6.1, pentru a se corecta distorsiunea. Astfel, formula modificata pentru cazurile (reale) in care σ este necunoscut si n > 30 este urmatoarea:

Formula 6.2

Inlocuirea lui cu reprezinta corectia ceruta de faptul ca s este un estimator distorsionat.

Pentru ilustrare, sa presupunem ca venitul mediu al unui esantion aleatoriu cu n = 500 este de 5000000 de lei () cu s = 125000. Care este intervalul de incredere estimat pentru media aritmetica a populatiei respective, la un nivel de incredere de 95% (α = 0,05)?

5000000 1,96 5595,34 =

= 5000000 10967

Pe baza mediei aritmetice a esantionului, estimam ca media aritmetica a veniturilor populatiei este cuprinsa intre 4989033 lei (5000000 10967) si 5010967 lei (5000000 10967) si exista doar 5% sanse ca acest interval sa nu contina media aritmetica a populatiei.

Atunci cand esantioanele sunt mici (n 30) si valoarea lui σ este necunoscuta, distributia normala standard nu poate fi folosita pentru a descrie distributia de esantionare a mediilor aritmetice. Pentru a construi intervale estimate semnificative in cazul n 30 se foloseste o alta distributie teoretica: distributia t Student[1]. Ca si in cazul distributiei normale, graficul distributiei t Student, numit si curba t, este simetric si are forma de clopot cu ambele extremitati extinse la infinit. Spre deosebire de graficul distributiei normale, forma exacta a graficului distributiei t depinde de dimensiunea esantionului. Pentru esantioane mici, graficul distributiei t este mult mai aplatizat decat cel al distributiei normale (comparati figura urmatoare cu oricare dintre graficele de mai sus).

Figura 6.2 Un exemplu de curba t

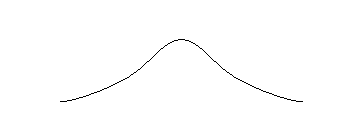
Pe masura ce dimensiunea esantionului creste, distributia t seamana din ce in ce mai mult cu distributia normala, identificandu-se cu aceasta pentru esantioane practic foarte mari (si teoretic infinite). Astfel, intrucat exista o distributie t specifica pentru fiecare esantion de dimensiune data, distributia t este, de fapt, o familie de distributii.

Distributia t particulara ceruta pentru rezolvarea unei anumite probleme depinde de un concept matematic numit grade de libertate. Acest concept se refera la numarul de valori libere sa varieze intr-o distributie. De pilda, daca stim ca o distributie de cinci scoruri are media aritmetica egala cu 3 si ca patru dintre aceste scoruri sunt 1, 2, 3, si 4, atunci valoarea celui de-al cincilea scor este fixata: 5. In general, pentru media aritmetica a unui esantion de dimensiune n, o distributie are n 1 grade de libertate. Fiecare distributie t este asociata cu un numar unic de grade de libertate. Mai precis, daca se selecteaza toate esantioanele posibile de dimensiune n dintr-o populatie normala, atunci distributia de esantionare a cantitatii

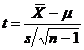
este distributia t Student cu n 1 grade de libertate.

Distributia t va fi utilizata indeosebi in testarea ipotezelor. Deocamdata vom descrie tabelul valorilor critice ale distributiei t, prezentat in Anexa C, si vom ilustra utilizarea acestui tabel pentru estimarea intervalelor. Schema generala a acestui tabel este prezentata in figura 6.3.

Figura 6.3 Schema tabelului valorilor critice ale distributiei t

Tabelul valorilor critice ale distributiei t specifica valorile pentru t_α, ceea ce inseamna valorile lui t pentru care aria aflata la dreapta sub curba t este egala cu α:

Nivelele α sunt dispuse pe primul rand al tabelului Valorile t_α sunt date pentru grade de libertate (gl), dispuse pe prima coloana din stanga, de la 1 la 30 si apoi 40, 60, 120 si . De notat ca, pe masura ce numarul de grade de libertate creste, diferenta dintre distributia t si distributia normala descreste, precum si ca pentru o infinitate de grade de libertate, distributia t este identica cu distributia normala. Pentru estimarea intervalelor, ca si pentru alte scopuri, avem nevoie de t_α/2. Aceasta valoare se localizeaza inmultind cu 2 valoarea α aflata pe primul rand. De pilda, pentru n = 30 si α = 0,05, numarul de grade de libertate este 29; la intersectia coloanei de sub t_α = 0,025 si liniei corespunzatoare pentru gl = 29 gasim valoarea 2,045. Astfel, in acest caz, vom spune ca valoarea lui t_α/2 este 2,045.

Formula pentru cazurile in care σ este necunoscut si n 30 este urmatoarea:

Formula 6.3

Pentru ilustrare, sa presupunem ca un esantion aleatoriu de 20 de adolescenti cu dificultati de invatare au obtinut urmatoarele rezultate la un test de cunostinte la care scorul maxim ce poate fi obtinut este de 40:

Tabelul 6.2 Scoruri obtinute la un test de cunostinte

de catre 20 de adolescenti cu dificultati de invatare

Presupunand ca variabila masurata este normal distribuita in populatia de adolescenti cu dificultati de invatare, care este intervalul de incredere estimat pentru media aritmetica a acestei populatii, la un nivel de incredere de 99%? Calculam mai intai media aritmetica a scorurilor din esantion:

=

Abaterea standard la nivelul esantionului este:

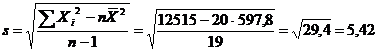
Pentru n = 20, numarul de grade de libertate este 19; avand α = 0,01, la intersectia coloanei de sub t_α = 0,005 si liniei corespunzatoare pentru gl = 19 gasim valoarea 2,861. Astfel, valoarea lui t_α/2 este 2,861. Aplicand formula 6.3, obtinem:

Astfel, estimam ca media aritmetica pe care o cautam este cuprinsa intre 21,03 si 27,91 si exista doar 1% sanse ca acest interval sa nu contina media aritmetica a populatiei.

De retinut ca formula 6.3 poate fi aplicata doar daca variabila de interes este normal distribuita.