
|
|
|
Media este tendinta centrala a rezultatelor constatate intr-o experienta
Este o masura a impreciziei unui set de date, exprima cat sunt de departate datele de media lor.
Deviatia Standard (DS) si multiplii ei au o importanta practica deosebita. Conform teoriei 95% dintre valori cad in intervalul -2DS +2DS, iar intre -3DS si 3DS cad restul pana la 99%. Intre -4DS si +4DS cade intregul set de valori. DS se exprima in unitatile de masura ale datelor. Impartind procenutal DS la medie obtinem coeficientul de variatie (CV) exprimat in procente. De obicei,pentru un analit urmarim sa obtinem un CV sub o anumita limita acceptata (Ex: glicemie sub 15%). (De fapt cifra 2 si 3 sunt aproximari ale valorilor de 1.96 si 2.58 care sunt adevaratele limite. In practica insa se obisnuieste sa se noteze 2DS si 3DS din comoditate)
Imprecizia masoara cat de 'imprastiate' ne este seria de date iar acuratetea ne arata cat de aproape suntem de valoarea reala a probei.
Imaginea de mai jos este concludenta pentru aceasta
diferenta care uneori scapa: 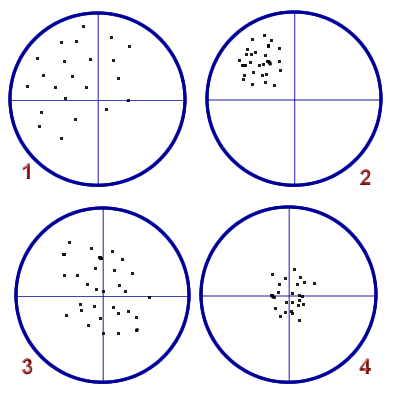
Astfel in figura 4 seria de date (reprezentata prin puncte) este atat precisa (punctele sunt grupate) cat si cu acuratete mare (fiind 'pe tinta')
In figura 2 se observa o serie la fel de preisa (valorile sunt grupate strins in jurul mediei) dar acuratetea seriei este scazuta, putine valori se apropie de target (Poate fi efectul unei erori sistematice)
Figura 3 reprezinta o serie de valori cu acuratete buna (media este pe tinta) dar cu precizia slaba, dispersia valorilor fiind destul de mare
Figura 1 reprezinta cazul cel mai rau, o serie de date care are si o precizie mica dar si o acuratete scazuta.
Problema semnificatiei unei medii se pune atunci cand vrem sa estimam media unei populatii prin media esantionului studiat. In cazul nostru (cand examinam o singura proba) ne-ar interesa valorile intre care ar putea varia media daca am mai efectua n masuratori (unde n este mare spre infinit). Acest interval se numeste intervalul de incredere al mediei. Acesta depinde de volumul esantionului si de distributia lui.
Intervalul se calculeaza pentru o anumita probabilitate p (p=sansa ca media sa nu se afle intre limitele calculate). p ia valori de obicei de 0,05 (adica 95% sanse ca media noastra este in intervalul calculat) si p=0,01 (echivalent cu sansa ca 99% media este in intervalul calculat)
De exemplu daca avem un set de date cu volum mic si dispersie mare nu vom putea afirma cu foarte mare siguranta ca media calculata este si cea adevarata.
Acest tip de harta dateaza din anii 1950 cand Levey si Jennings au introdus metoda controlului statistic in laboratoarele medicale. Metoda lor se bazeaza pe studiile lui Walter A. Shewhart un statistician care lucra la Bell Telephone Laboratories.
Pe aceste harti se aplica regulile lui Westgard.
Elementele constitutive ale unei harti Levey Jennings
Presupunem ca avem un set de date, in cazul nostru un set de valori reprezentand concentratia zilnica ale aceluiasi produs. Calculam media si deviatia standard.
Pe axa Ox se pun zilele sau numarul probei
Paralel cu axa Ox se inscriu drepte reprezentand valorile mediei si a +1DS, +2DS,+3DS, -1DS,-2DS,-3DS.
Fiecare punct este reprezentat direct pe graficul astfel obtinut.
O imagine a unei harti Levey Jennings desenata de LabWorks este prezentata mai jos. Se observa cu usurinta elementele enumerate mai sus.
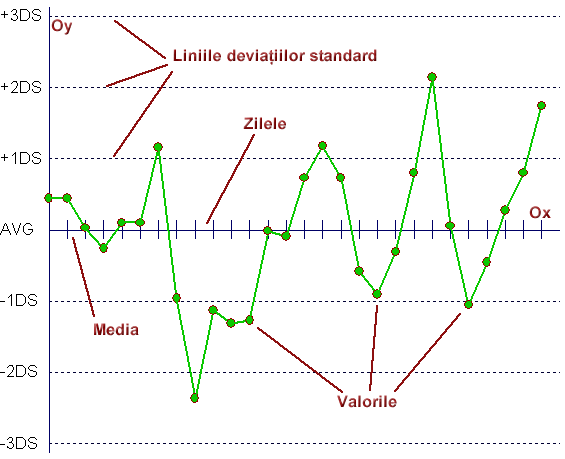
Harta se poate complica prin adaugarea altor valori importante pentru noi (Valorile in cifre pe axe, observatiile de la fiecare proba sau regulile Westgard pe care le incalca)
Aceasta harta are o expresivitate mare, mai ales interpretata in contextul valorilor pentru medie si dispersie.
Majoritatea analizoarelor mai noi alcatuiesc automat o astfel de harta pentru rezultatele controlului intern pe ultimele 30 zile.
Totusi harta LJ are limitarile ei. De exemplu, putem avea un interval in care sa apara o eroare sistematica in plus, apoi o perioada aproximativ la fel de lunga in care sa apara o eroare sistematica in minus. In urma calculelor statistice se observa o dispersie si un coeficient de variatie mai mare dar media poate sa fie foarte aproape de valoarea reala a materialului de control. Din pacate este aproape imposibil sa se deceleze acest lucru pe o harta Levey Jennings. Limitarea aceasta este suplinita de harta Cumulative Sums (CUSUM)
Aceasta harta vine ca o completare la analiza standard folosind metoda Levey Jennings. Aparuta relativ recent nu este implementata decat rar in analizoare sau alte soft-uri de analiza. LabWorks permite trasarea imediata a acestei harti.
Dupa cum am spus harta este sensibila la detectarea erorilor sistematice. Sa vedem cum desenam o astfel de harta.
Avem setul de date precum si valoarea reala (sau valoarea predeterminata) a materialului de control. Efectuam o diferenta algebrica (pastram semnul) dintre valoarea obtinuta de noi si cea reala. Apoi, pentru fiecare proba insumam aceasta diferenta cu rezultatul calculat la pasul anterior. Rezultatul se reprezinta ca un punct avand coordonatele calculate (pe Oy), coodronata Ox fiind ziua sau numarul probei.
S(i)=S(i-1)+(Xi - Xm) unde S(k) este rezultatul, S(k-1) este valoarea calculata la pasul precedent, Xi este valoarea obtinuta pentru ziua i iar Xm este valoarea predeterminata.
Pentru exemplificare aratam o astfel de harta pe un set de date care prezinta exact genul de erori sistematice descrise mai sus.
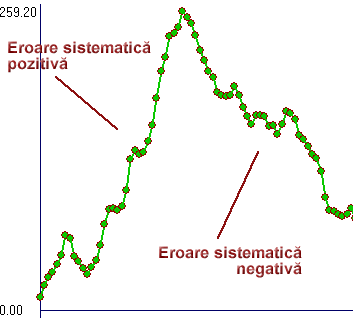
Se observa 2 tipuri de erori sistematice.
In cazul in care nu exista o astfel de eroare graficul nostru va oscila in jurul valorii de 0 deoarece erorile intamplatoare se vor neutraliza ('media' lor fiind prin definitie 0)
Astfel medicul specialist va putea sa caute in preajma zilei din varf conditiile care au dus la schimbarea trend-ului si sa ia masuri. Deasemenea, la observarea unui trend crescator sau descrescator acesta trebuie interpretat ca un semnal de alarma. (alaturi de alte reguli)