
|
|
|
ELEMENTE DE ANALIZA MULTIVARIATA
Unele situatii de cercetare necesita analiza mai multor variabile, chiar daca cercetatorul este interesat in principal de o anumita corelatie bivariata. Tehnicile prezentate in aceasta sectiune se refera la corelatia multivariata dintre variabile masurate la nivel de interval sau de raport si se bazeaza pe coeficientul r al lui Pearson.
1 CORELATIA PARTIALA
Metoda corelatiei partiale poate fi folosita atunci cand cercetatorul doreste sa observe influenta unei a treia (a patra etc.) variabile asupra unei corelatii bivariate. In cele ce urmeaza vom folosi urmatoarele simboluri, numite coeficienti de corelatie partiala de ordinul zero:
ryz = coeficientul de corelatie dintre variabila Y si variabila Z
rxy = coeficientul de corelatie dintre variabila X si variabila Y
rxz = coeficientul de corelatie dintre variabila X si variabila Z
Acesti coeficienti se calculeaza cu formula 16, facand inlocuirile corespunzatoare.
Atunci cand controlam influenta unei singure variabile X asupra corelatiei dintre variabilele Y si Z folosim simbolul ryzx, numit coeficient de corelatie partiala de ordinul intai. ryzx se refera la coeficientul de corelatie partiala dintre variabilele Y si Z sub influenta variabilei X ("variabila de control"). ryzx se calculeaza cu ajutorul urmatoarei formule:
Formula 18 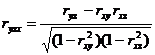
Pentru ilustrare, sa consideram datele din tabelul 11, in care se prezinta distributia a trei variabile, X, Y si Z, impreuna cu valorile partialilor de ordinul zero. Sa presupunem ca ne intereseaza influenta variabilei X asupra corelatiei dintre Y si Z.
Tabelul 11 O ilustrare a corelatiei partiale
X
Y
Z
2
12
4
7
14
10
8
18
8
4
15
9
5
14
7
ryz = 0,50 rxy = 0,78 rxz = 0,70
Valoarea ryz = 0,50 indica o corelatie pozitiva moderata intre variabilele Y si Z. Aplicand formula 18, obtinem:

Aceasta valoare a coeficientului partial de ordinul intai este mult mai mica decat valoarea coeficientului partial de ordinul zero ryz = 0,50. Acest rezultat, pe care il vom nota prin ryzx << ryz, arata ca daca eliminam influenta variabilei X asupra variabilelor Y si Z, corelatia dintre variabilele Y si Z se reduce de la 0,5 la aproape 0. Intr-un astfel de caz, se poate ca X sa determine atat variatia lui Y, cat si variatia lui Z, relatia dintre Y si Z fiind inautentica (aparenta) sau ca variabilele Y si Z sa fie corelate, dar nu direct, ci prin intermediul variabilei X:

X
Z
![]()
![]()
 sau
sau
Z
In exemplul nostru, valorile rxy = 0,78 si rxz = 0,70 pot fi luate drept un indiciu probabil al tipului de relatie reprezentat prin diagrama din stanga. De notat ca distinctia dintre cele doua tipuri de relatie nu poate fi facuta cu precizie doar pe baza metodelor statistice. Intr-o situatie reala de cercetare, distinctia se poate face pe criterii de continut al cercetarii respective (ordinea temporala dintre variabile s.a).
Un al doilea tip de rezultat posibil este acela in care ryzx si ryz au valori apropiate. Acest rezultat, pe care il vom nota prin ryzx ryz, arata ca daca eliminam influenta variabilei X asupra variabilelor Y si Z, corelatia dintre variabilele Y si Z ramane neschimbata, sau, altfel spus ca X nu influenteaza semnificativ corelatia dintre Y si Z, relatia dintre variabilele Y si Z fiind directa.
Al treilea tip de rezultat posibil este acela in care valoarea lui ryzx este mult mai mare decat valoarea lui ryz. Acest rezultat, pe care il vom nota prin ryzx >> ryz, arata ca variabila luata initial drept independenta si variabila de control (X) au fiecare in parte o influenta separata asupra variabilei dependente si nu sunt corelate una cu alta. Urmatoarea diagrama prezinta acest tip de relatie pentru cazul in care Z este variabila dependenta:
Daca se obtine acest rezultat, concluzia este ca atat Y, cat si X sunt variabile independente, iar urmatoarea etapa in analiza statistica este, probabil, utilizarea regresiei multiple si a corelatiei multiple. Metoda regresiei multiple permite izolarea influentelor separate ale mai multor variabile independente asupra variabilei dependente si astfel permite identificarea variabilei independente care are cea mai puternica influenta asupra variabilei dependente, iar metoda corelatiei multiple permite evidentierea influentelor combinate ale tuturor variabilelor independente asupra variabilei dependente.
2 REGRESIA MULTIPLA
Ecuatia de regresie poate fi modificata pentru a include (teoretic) un numar oricat de mare de variabile independente. Aceasta tehnica statistica se numeste regresie multipla. In cazul a doua variabile independente, linia de regresie multipla este descrisa de urmatoarea formula, numita ecuatia de regresie multipla:
Formula 19 ![]()
in care b1 = panta partiala a corelatiei dintre prima variabila independenta si Y
b2 = panta partiala a corelatiei dintre a doua variabila independenta si Y
Parametrii b1 si b2 se calculeaza cu ajutorul urmatoarelor formule:
Formula 20 ![]()
Formula 21 ![]()
in care sy = abaterea standard a variabilei Y
s1 = abaterea standard a variabilei independente X1
s2 = abaterea standard a variabilei independente X2
r1y = coeficientul de corelatie dintre X1 si Y
r2y = coeficientul de corelatie dintre X2 si Y
r12 = coeficientul de corelatie dintre X1 si X2
Pentru a ilustra calcularea parametrilor b1 si b2, sa consideram datele din tabelul 12, in care, pentru un esantion de 15 subiecti, se prezinta scorurile obtinute inaintea unui test (X1), numarul mediu de raspunsuri corecte date la sase incercari preliminare (X2) si scorurile post-test (Y).
Tabelul 12 O ilustrare pentru doua variabile independente
X1
X2
Y
15
7,70
36
22
8,20
39
16
7,80
35
19
9,30
43
22
8,20
40
20
8,80
42
28
12,10
49
14
8,00
38
18
8,10
36
21
11,20
44
26
9,40
35
14
10,30
43
19
8,50
37
22
7,60
41
20
8,40
40
s1 = 4,06
s2 = 1,34
s3 = 3,92
r1y = 0,39 r2y = 0,77 r12 = 0,45
Aplicand formulele 20 si 21, obtinem:
![]()
![]()
Parametrul a se calculeaza cu ajutorul urmatoarei formule:
Formula 22 ![]()
In exemplul nostru, avem:
![]()
![]()
![]()
![]()
In fine, ecuatia de regresie multipla pentru exemplul nostru este:
![]()
Acum, sa presupunem ca ne intereseaza sa prezicem scorul post-test al unui subiect cu scorul pre-test de 25 si media raspunsurilor corecte la incercarile preliminare de11,16. Folosind ecuatia de regresie multipla din exemplul nostru pentru X1 = 25 si X2 = 11,16 obtinem:
![]()
Prin urmare, prezicem ca un subiect cu scorurile X1 = 25 si X2 = 11,16 va obtine un scor post-test de 4
In cele ce urmeaza prezentam o modalitate simplificata de utilizare a metodei regresiei multiple pentru evaluarea influentelor separate ale variabilelor dependente asupra variabilei dependente. Pentru o astfel de evaluare se considera scorurile standardizate ale variabilelor si se utilizeaza coeficientii de regresie standardizati, simbolizati in general prin β. Aceste marimi, numite si "pante partiale standardizate", arata cantitatea de schimbare a abaterii standard a variabilei Y corespunzatoare unei unitati de schimbare a abaterii standard a unei variabile independente, in timp ce influentele celorlalte variabile independente sunt controlate. In cazul a doua variabile independente, acesti coeficienti se calculeaza cu ajutorul urmatoarelor formule:
Formula 23 ![]()
Formula 24 ![]()
in care β1 = panta partiala standardizata a corelatiei dintre X1 si Y
β2 = panta partiala standardizata a corelatiei dintre X2 si Y
Ecuatia de regresie multipla standardizata este data de urmatoarea formula:
Formula 24 ![]()
in care simbolul Z arata ca toate scorurile au fost standardizate. Amintim ca formula de calcul pentru standardizarea scorurilor unui esantion este
![]()
Acum,
formula 24 poate fi simplificata, intrucat definitia algebrica a
parametrului az este ![]() si, dupa cum
stim, media aritmetica a oricarei distributii standardizate
de scoruri este 0. Ca atare, az se reduce la 0, astfel
ca pentru ecuatia de regresie multipla standardizata putem
folosi urmatoarea formula:
si, dupa cum
stim, media aritmetica a oricarei distributii standardizate
de scoruri este 0. Ca atare, az se reduce la 0, astfel
ca pentru ecuatia de regresie multipla standardizata putem
folosi urmatoarea formula:
Formula 25 ![]()
Pentru exemplul de mai sus, valorile coeficientilor de regresie standardizati sunt:

Astfel, ecuatia de regresie multipla standardizata pentru acest exemplu este:
![]()
Concluzia este ca variabila X2 are o influenta mult mai puternica asupra variabilei dependente decat variabila X1, astfel ca predictiile asupra scorurilor standardizate Zy nu vor fi influentate semnificativ de scorurile Z1.
Inspectarea datelor din tabelul 12 ofera unele indicii privind explicatia rezultatului obtinut. Astfel, putem observa ca X2 este puternic corelata cu Y (r2y = 0,77), in timp ce X1 prezinta o corelatie slaba pana la moderat cu Y (r1y = 0,39).
De notat ca daca am fi obtinut β1 >> β2, am fi tras concluzia ca variabila X1 are o influenta mult mai puternica asupra variabilei dependente decat variabila X2, iar daca am fi obtinut β1 β2, am fi tras concluzia ca cele doua variabile independente au aproximativ aceeasi influenta asupra variabilei dependente.
3 CORELATIA MULTIPLA
Metoda corelatiei multiple permite evidentierea influentelor combinate ale tuturor variabilelor independente asupra variabilei dependente. Pentru aceasta, se calculeaza coeficientul de corelatie multipla R si coeficientul de determinare multipla R2.
O formula de calcul pentru coeficientul R in cazul a doua variabile independente este urmatoarea:
Formula 26 ![]()
Pentru datele din exemplul de mai sus, avem:
![]()
Acest rezultat indica o corelatie puternica intre influentele combinate ale variabilelor X1 si X2 si variabila Y.
Coeficientul de determinare multipla R2 se interpreteaza in acelasi fel ca si coeficientul de determinare bivariata r2. In exemplul nostru, R2 = 0,59, ceea ce arata ca influenta combinata a celor doua variabile independente explica aproximativ 59%din variatia totala a scorurilor post-test, restul de 41% din aceasta variatie datorandu-se probabil influentei altor variabile, erorilor de masurare sau intamplarii.
GLOSAR
Coeficientul d al lui Somer: marime asimetrica a corelatiei adecvata pentru cazul a doua variabile masurate la nivel ordinal cu un numar mic de valori.
Coeficientul de contingenta C: marime a corelatiei bazata pe χ2, adecvata pentru cazul a doua variabile masurate la nivel nominal; se recomanda calcularea acestui coeficient numai pentru tabele de mare dimensiune.
Coeficientul r al lui Pearson: marime a corelatiei lineare dintre doua variabile masurate la nivel de interval sau de raport.
Coeficientul V al lui Cramer: marime a corelatiei bazata pe χ2, adecvata pentru cazul a doua variabile masurate la nivel nominal; se recomanda calcularea acestui coeficient numai pentru tabele mai mari de 2 2.
Coeficientul γ: marime simetrica a corelatiei adecvata pentru cazul a doua variabile masurate la nivel ordinal cu un numar mic de valori.
Coeficientul ρ al lui Spearman: marime a corelatiei adecvata pentru cazul a doua variabile masurate la nivel ordinal cu o amplitudine relativ larga de scoruri diferite si putine cazuri legate in privinta fiecarei variabile.
Coeficientul τb al lui Kendall: marime simetrica a corelatiei adecvata pentru cazul a doua variabile masurate la nivel ordinal cu un numar mic de valori; se recomanda calcularea acestui coeficient numai pentru tabele patratice.
Coeficientul φ: marime a corelatiei bazata pe χ2, adecvata pentru cazul a doua variabile masurate la nivel nominal; se recomanda calcularea acestui coeficient numai pentru tabele 2 2.
Corelatie: relatie intre doua sau mai multe variabile; se spune ca doua variabile sunt corelate daca distributia scorurilor uneia dintre acestea se schimba sub influenta scorurilor celeilalte.
Corelatie negativa: corelatie intre doua variabile caracterizata prin aceea ca scoruri inalte ale unei variabile sunt asociate cu scoruri joase ale celeilalte variabile sau, altfel spus, variabilele variaza in sensuri opuse.
Corelatie pozitiva: corelatie intre doua variabile caracterizata prin aceea ca scoruri inalte ale unei variabile sunt asociate cu scoruri inalte ale celeilalte variabile, iar scoruri joase ale unei variabile sunt asociate cu scoruri joase ale celeilalte variabile sau, altfel spus, variabilele variaza in acelasi sens.
Corelatie liniara: corelatie intre doua variabile de interval sau de raport caracterizata prin aceea ca dispunerea punctelor in diagrama de imprastiere poate fi aproximata printr-o linie dreapta.
Corelatie perfecta: corelatia dintre doua variabile caracterizata prin aceea ca fiecare scor al unei variabile este asociat cu un singur scor al celeilalte variabile.
Diagrame de imprastiere: modalitati de prezentare vizuala a corelatiei dintre doua variabile masurate la nivel de interval sau de raport.
Ecuatia de regresie bivariata: ecuatie care descrie matematic o linie de regresie.
Linie de regresie: linie dreapta care rezuma cel mai bine corelatia dintre doua variabile de interval sau de raport.
Marimile corelatiei: marimi statistice care permit cuantificarea importantei (tariei) unei relatii dintre variabile.
Metoda corelatiei multiple: tehnica multivariata de evidentiere a influentelor combinate ale tuturor variabilelor independente asupra variabilei dependente.
Metoda corelatiei partiale: tehnica multivariata de evidentiere a influentei unei a treia (a patra etc.) variabile asupra unei corelatii bivariate.
Metoda regresiei multiple: tehnica multivariata care permite izolarea influentelor separate ale mai multor variabile independente asupra variabilei dependente si astfel permite identificarea variabilei independente care are cea mai puternica influenta asupra variabilei dependente.
Predictie: apreciere a scorurilor unei variabile pe baza cunoasterii scorurilor in privinta altei variabile; o predictie este cu atat mai precisa, cu cat corelatia dintre cele doua variabile este mai puternica.