Testul scorurilor z pentru diferenta dintre doua medii aritmetice

TESTUL SCORURILOR Z  PENTRU DIFERENTA DINTRE DOUA MEDII ARITMETICE

Testul expus in aceasta sectiune este aplicabil daca, pe langa independenta esantioanelor, sunt satisfacute urmatoarele doua conditii (i) nivelul de masura al variabilei de interes este de interval sau de raport si (ii) cele doua esantioane sunt relativ mari, ceea ce inseamna n₁ > 30 si n₂ > 30.

Distributia de esantionare la care ne vom referi in continuare este distributia de esantionare a diferentelor dintre mediile aritmetice ale esantioanelor, despre care se demonstreaza ca este normala daca distributiile de esantionare separate ale mediilor aritmetice ale esantioanelor sunt normale. Teorema limitei centrale garanteaza ca aceste distributii de esantionare aproximeaza cu atat mai bine normalitatea, cu cat dimensiunile esantioanelor sunt mai mari. Astfel, atunci cand esantioanele sunt mari, pentru descrierea acestei distributii de esantionare se poate folosi distributia Z.

Ipoteza de nul este si in acest caz un enunt de tipul "nici o diferenta", numai ca este vorba despre diferenta dintre doua populatii sub aspectul variabilei de interes. Astfel, forma ipotezei de nul este H₀: μ₁ = μ₂ sau, echivalent, H₀: μ₁ μ₂ = 0.

Ipoteza alternativa corespunde tipului de test, bilateral sau unilateral, intentionat de cercetator. Pentru un test bilateral, ipoteza alternativa este de forma H_a: μ₁ μ₂. Daca testul este unilateral, atunci ipoteza de nul poate lua una dintre urmatoarele doua forme:

H_a: μ₁ > μ₂

H_a: μ₁ < μ₂

Prima forma corespunde unui test unilateral in care intreaga zona critica este plasata in extremitatea dreapta a distributiei de esantionare, iar cea de-a doua forma corespunde unui test unilateral in care intreaga zona critica este plasata in extremitatea stanga a distributiei de esantionare. Daca rezultatul statisticii testului cade in zona critica, atunci ipoteza de nul poate fi respinsa, fiind acceptata ipoteza diferentei sub aspectul variabilei de interes.

Teoretic, formula de calcul al testului scorurilor Z pentru diferenta dintre doua medii aritmetice este urmatoarea:

Formula 1

in care = diferenta dintre mediile aritmetice ale esantioanelor

μ₁ - μ₂ = diferenta dintre mediile aritmetice ale populatiilor

= abaterea standard a distributiei de esantionare a diferentelor dintre

mediile aritmetice ale esantioanelor

In formula 1, cel de-al doilea termen al numaratorului, μ₁ - μ₂, este necunoscut. Acest termen se reduce insa la zero, intrucat testul are loc sub presupunerea ca ipoteza de nul, μ₁ μ₂ = 0, este adevarata. Mai departe, pentru esantioane mari, distributia de esantionare a diferentelor dintre mediile aritmetice ale esantioanelor se defineste astfel:

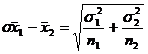
Intrucat valorile abaterilor standard ale populatiilor, σ₁ si σ₂, nu sunt aproape niciodata cunoscute, se utilizeaza abaterile standard ale esantioanelor, cu corectiile corespunzatoare pentru distorsiune. Astfel, formula folosita pentru estimarea abaterii standard a distributiei de esantionare in aceasta situatie este urmatoarea:

Formula 2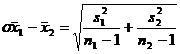

Prin urmare, vom lucra practic cu formula urmatoare pentru Z (obtinut):

Formula 3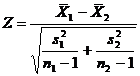

Ca si pana acum, vom considera un exemplu. Un cercetator presupune ca barbatii si femeile difera sub aspectul capacitatii de rezolvare de probleme. Pentru a verifica aceasta ipoteza, cercetatorul alcatuieste un esantion aleatoriu de 127 de subiecti si le administreaza un test de rezolvare de probleme. Esantionul este apoi impartit in doua subesantioane dupa criteriul sex, iar marimile statistice sunt calculate pentru fiecare subesantion, datele obtinute fiind urmatoarele:

Presupunand ca testul de rezolvare de probleme furnizeaza date de interval sau de raport, se poate aplica testul scorurilor Z pentru semnificatia diferentei dintre doua medii aritmetice. Se poate observa ca scorul mediu al esantionului 1 este mai mic decat cel al esantionului 2. Prin aplicarea testului mentionat se poate afla daca aceasta diferenta este suficient de mare pentru a indreptati concluzia ca exista o diferenta semnificativa intre barbati si femei sub aspectul capacitatii de rezolvare de probleme si nu o interventie a unor factori intamplatori.

Pasul 1. Enuntarea ipotezelor

H₀: μ₁ = μ₂

H_a: μ₁ μ₂

Pasul 2. Selectarea distributiei de esantionare si stabilirea zonei critice

Distributia de esantionare = Distributia Z

α = 0,05 (test bilateral)

Z_α/2 (critic) = 1,96

Pasul 3. Calcularea statisticii testului

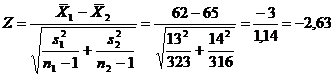
Pasul 4. Luarea deciziei

Intrucat Z (obtinut) se afla in zona critica ( 2,63 < 1,96), ipoteza de nul poate fi respinsa, ceea ce reprezinta o dovada in sprijinul ipotezei ca barbatii si femeile difera sub aspectul capacitatii de rezolvare de probleme. Decizia de a respinge ipoteza de nul are o probabilitate de doar 0,05 de a fi gresita.