Marimile tendintei centrale

MARIMILE TENDINTEI CENTRALE

Marimile folosite in mod obisnuit pentru masurarea tendintei centrale sunt media aritmetica, mediana si modul. Fiecare dintre aceste marimi rezuma o intreaga distributie de scoruri, descriind cea mai tipica sau centrala valoare a distributiei respective sub forma unui singur numar sau a unei singure categorii.

1 MEDIA ARITMETICA

Media aritmetica se calculeaza doar pentru variabile masurate la nivel de interval sau de raport si se defineste ca rezultat al impartirii sumei tuturor scorurilor dintr-o multime de scoruri la numarul total de scoruri din acea multime. Simbolul folosit pentru media aritmetica a unui esantion este, iar pentru media aritmetica a unei populatii se foloseste litera greceasca μ (miu). Intrucat deocamdata va fi vorba numai despre esantioane, vom folosi simbolul . Formula matematica a mediei aritmetice este urmatoarea:

Formula 3.1 =

in care = suma scorurilor

n = numarul total de scoruri.

Sa presupunem, de pilda, ca am inregistrat varstele pentru un esantion de 11 persoane si ca am obtinut urmatoarea distributie de frecvente:

Tabelul 3.1 Varstele pentru un esantion de 11 persoane

Sa remarcam ca avem 11 scoruri, cate unul pentru fiecare persoana din esantion. Pentru a afla media aritmetica a varstelor persoanelor din esantion sau, pe scurt, varsta medie, trebuie sa insumam toate cele 11 scoruri si sa impartim rezultatul obtinut la 11. Pentru a scurta procedura, inmultim fiecare scor cu frecventa cu care apare, adunam rezultatele inmultirilor si impartim suma astfel obtinuta la 11:

Astfel, media aritmetica a varstelor persoanelor din esantionul considerat este 19.

Media aritmetica este marimea statistica folosita cel mai des in aprecierea tendintei centrale a unei multimi de scoruri de interval sau de raport deoarece este usor de calculat si in plus are urmatoarele proprietati importante, pe care le vom folosi in unele aplicatii ulterioare.

1. Pentru orice distributie de scoruri, suma abaterilor scorurilor de la media lor aritmetica este egala cu zero. Abaterea unui scor X_i fata de media aritmetica este diferenta X_i - , astfel ca aceasta proprietate se exprima simbolic dupa cum urmeaza:

-) = 0

In cuvinte, suma diferentelor dintre scoruri si media lor aritmetica este egala cu 0. Aceasta proprietate, care este folosita in obtinerea unor formule statistice mai complicate, poate fi exprimata si spunand ca pentru orice distributie de scoruri, media aritmetica este punctul in jurul caruia toate scorurile se anuleaza, ceea ce face din media aritmetica o marime descriptiva adecvata in masurarea centralitatii scorurilor.

2. Pentru orice distributie de scoruri, suma patratelor abaterilor scorurilor fata de media lor aritmetica este mai mica decat suma patratelor abaterilor scorurilor fata de oricare alt scor din distributie, in simboluri:

-)² < - X_j)²

In cuvinte, suma patratelor diferentelor dintre scoruri si media lor aritmetica este mai mica decat suma patratelor diferentelor dintre scoruri si oricare alt scor din distributie. Aceasta proprietate, care este folosita pentru a defini unele marimi ale dispersiei si pentru a calcula unele marimi ale corelatiei[1], poate fi exprimata si spunand ca media aritmetica este punctul in jurul caruia suma abaterilor patratice ale scorurilor este minima.

Tabelul 3.2 ilustreaza cele doua proprietati ale mediei aritmetice pentru distributia de scoruri din tabelul 3.1, in care = 19.

Tabelul 3.2 Proprietati ale mediei aritmetice

pentru datele din tabelul 3.1

Se poate constata ca suma abaterilor patratice ale scorurilor fata de media aritmetica (74) este mai mica decat suma abaterilor patratice ale scorurilor fata de scorul 17 (118). Aceasta relatie are loc pentru oricare alt scor din distributie.

Este important de retinut ca in cazul in care o distributie are foarte putine scoruri extreme (foarte mari sau foarte mici), media aritmetica poate deveni o marime inselatoare in aprecierea centralitatii. De pilda, multimea de scoruri 15, 20, 25, 30, 35 are media aritmetica 25, in timp ce media aritmetica a multimii 15, 20, 25, 30, 3500 este 718, iar media aritmetica a multimii 1, 15, 20, 25, 30, este 18,2. Se poate constata ca media aritmetica este afectata disproportionat de prezenta scorurilor 3500 si, respectiv, 1. Media aritmetica este "trasa" intotdeauna in directia scorurilor extreme, mai ales in directia celor relativ mari[2]. Acesta este un motiv pentru care se recurge uneori la o alta marime a tendintei centrale: mediana.

2 MEDIANA

Mediana poate fi determinata atat pentru variabile masurate la nivel de interval sau de raport, cat si pentru variabile masurate la nivel ordinal. Ca si in cazul mediei aritmetice, si in cazul medianei vom folosi doua simboluri: pentru mediana unui esantion si pentru mediana unei populatii. De asemenea, intrucat deocamdata va fi vorba numai despre esantioane, vom folosi simbolul .

Mediana a unei multimi de scoruri este "punctul de mijloc" al acelei multimi, in sensul ca numarul de cazuri cu scoruri mai mici sau egale cu este egal cu numarul de cazuri cu scoruri mai mari sau egale cu . Pentru a afla mediana unei multimi de n scoruri, scorurile respective se aranjeaza mai intai in ordine crescatoare sau descrescatoare. Daca n este impar, atunci mediana este, evident, scorul cazului de mijloc. Daca n este par, atunci vor fi doua cazuri de mijloc si orice valoare cuprinsa intre cele doua scoruri ale cazurilor de mijloc satisface definitia medianei. Intr-un astfel de situatie, daca scorurile sunt de interval sau de raport, prin conventie, se ia drept mediana media aritmetica a celor doua scoruri ale cazurilor de mijloc.

In exemplu din tabelul 3.1 avem de-a face cu 11 cazuri. Varsta mediana este 18, deoarece avem in esantion cinci persoane cu varste mai mici de 18 ani si cinci persoane cu varste mai mari de 18 ani. Sa presupunem acum ca am inregistrat varstele pentru un esantion de 7 persoane si ca am obtinut urmatoarea distributie de frecvente:

Tabelul 3.3 Varstele pentru un esantion de 7 persoane

Pentru datele din acest tabel, = 29: trei persoane au varste mai mici de 29 de ani si alte trei persoane au varste mai mari de 29 de ani. De remarcat ca varsta tipica a persoanelor din acest esantion este mai bine reprezentata de varsta mediana decat de media aritmetica a varstelor, 33, care este "trasa" in sus de scorul 60. Acum, daca adaugam la acest esantion o persoana de 31 de ani, avem 8 cazuri cu scorurile 26, 26, 28, 29, 30, 31, 32 si 60. Astfel, apar doua cazuri de mijloc, unul cu scorul 29 si celalalt cu scorul 30, si orice numar cuprins intre aceste doua scoruri satisface definitia medianei. Ca atare, mediana este media aritmetica a scorurilor celor doua cazuri de mijloc: 29,5.

Urmatoarele doua exemple arata de ce este inclusa expresia "sau egale" in definitia medianei. Sa presupunem ca am inregistrat numarul de copii pentru un esantion de 16 familii, rezultatele obtinute fiind urmatoarele:

Tabelul 3.4 Numarul de copii pentru un

esantion de 16 familii

In esantionul considerat in tabelul 3.4, 8 familii au 0, 1 sau 2 copii, iar celelalte 8 familii au cate 2 sau 3 copii, astfel ca cea de-a 8-a si cea de-a 9-a familie (cele doua cazuri de mijloc) au acelasi numar de copii: 2. Ca atare, mediana aceste multimi de scoruri este 2: 8 familii au fiecare un numar de copii mai mic sau egal cu 2, iar celelalte 8 familii au fiecare un numar de copii mai mare sau egal cu 2. Tot asa, in multimea impara de scoruri

1, 2, 3, 5, 5, 5, 7, 10, 12

scorul median este 5, caci avem patru scoruri mai mici sau egale cu 5 (1, 2, 3, 5) si patru scoruri mai mari sau egale cu 5 (5, 7, 10, 12).

Urmatorul exemplu ilustreaza determinarea medianei pentru variabile de nivel ordinal. Sa presupunem ca intr-o cercetare privind modul de petrecere a timpului liber, 11 subiecti au fost solicitati sa raspunda la intrebarea "Cat de des ati fost la cinematograf in ultimele sase luni?" Raspunsurile la aceasta intrebare au fost inregistrate pe o scala ordinala cu urmatoarele categorii: 1. Deloc, 2. Foarte rar, 3. Rar, 4. Des, 5. Foarte des. Aranjand scorurile in ordine descrescatoare, datele sunt urmatoarele:

Tabelul 3.5 "Cat de des mergeti la cinematograf?"

Avand un total de 11 cazuri, cazul de mijloc este al 6-lea, F, asa incat raspunsul median este scorul celui de-al saselea caz: Des. Daca adaugam un subiect care da raspunsul De loc, avem doua cazuri de mijloc: cel de-al 6-lea, F, si cel de-al 7-lea, G. In aceasta situatie, teoretic vorbind, orice raspuns intre Des si Foarte rar satisface definitia medianei. Practic, pe scala mentionata, intre Des si Foarte rar avem raspunsul Rar, pe care il vom considera drept raspuns median: 6 subiecti merg la cinematograf foarte des sau des, iar ceilalti sase subiecti merg la cinematograf foarte rar sau deloc.

Daca numarul de cazuri din esantion este relativ mic, identificarea cazului sau cazurilor de mijloc este neproblematica. Pentru esantioane mari, identificarea mentionata poate fi inlesnita prin folosirea unor calcule simple. Astfel, dupa ordonarea scorurilor, daca n este impar, cazul de mijloc este dat de formula ; daca n este par, primul caz de mijloc este dat de formula , iar cel de-al doilea caz de mijloc de formula . Ca exercitiu, determinati mediana scorurilor din tabelul 2.4 din capitolul anterior. (Puteti folosi tabelul 2.5? Daca da, cum?)

De notat ca mediana nu este "trasa" in directia valorilor extreme, deoarece aceasta marime ia in considerare doar ordinea scorurilor, nu si magnitudinea efectiva a acestora[3]. Reluand un exemplu dat mai sus, multimea de scoruri 15, 20, 25, 30, 35 are aceeasi mediana ca si multimea 15, 20, 25, 30, 3500: scorul 25. Sa mai remarcam ca mediana si media aritmetica ale unei multimi de scoruri pot sa coincida, acesta fiind, de pilda, cazul multimii 15, 20, 25, 30, 35.

Mediana nu poate fi determinata pentru variabile de nivel nominal, deoarece aceste variabile nu au scoruri care sa poata fi ordonate. Marimea tendintei centrale care poate fi folosita la nivel nominal, ca si la toate celelalte nivele de masura, este modul.

3 MODUL

Modul unei multimi de scoruri (Mo) este scorul care apare cel mai frecvent in acea multime. De pilda, modul datelor din tabelul 3.4 este 2, deoarece este scorul care apare de cele mai multe ori in esantionul considerat, iar modul datelor din tabelul 3.5 sau, altfel spus, raspunsul modal, este Foarte des, deoarece este raspunsul care apare de cele mai multe ori in raport cu celelalte raspunsuri.

Modul este singura marime care poate fi folosita in masurarea tendintei centrale pentru variabile de nivel nominal. Modul unei astfel de variabile este cea mai mare categorie a sa sau, altfel spus, categoria cu cele mai multe cazuri. De pilda, modul variabilei status marital pentru distributia din tabelul 2.10 din capitolul anterior este categoria Casatorit.

Exemplele date pana acum ilustreaza cazul multimilor unimodale de scoruri, adica a multimilor in care exista un singur scor care apare mai frecvent decat celelalte. Daca intr-o multime de scoruri exista doua astfel de scoruri, ca in exemplul

3, 3, 3, 5, 5, 5, 7, 10, 12,

atunci se spune ca multimea respectiva este bimodala. Desigur, este posibil ca o multime de scoruri sa aiba trei sau mai multe moduri, dupa cum este posibil ca o multime de scoruri sa nu aiba mod, fiecare scor din multimea respectiva aparand de un numar egal de ori. Pe de alta parte, este posibil ca o multime unimodala sa nu aiba modul localizat "la mijloc". Fie, de pilda, urmatoarea multime de scoruri:

44, 44, 46, 46, 46, 48, 50, 50, 50, 50, 50.

Modul aceste multimi este 50, in timp ce mediana este 48, iar media aritmetica este aproximativ 47,6. Pretentia ca modul este o marime a tendintei centrale trebuie sa fie inteleasa in sensul ca aceasta marime indica localizarea celei mai mari grupari sau concentrari de scoruri dintr-o multime unimodala, ceea ce se poate dovedi important in special pentru date de nivel nominal. Sa presupunem ca ultima multime de scoruri de mai sus reprezinta o inregistrare a masurilor sacourilor vandute intr-un magazin timp de o saptamana. Astfel, modul masurilor de sacouri vandute sau, altfel spus, masura modala a acestora este de mai mare interes pentru directorul magazinului decat mediana masurilor de sacouri vandute. Pe de alta parte, sa observam ca in acest caz, media aritmetica a scorurilor nu este in nici un fel semnificativa: numerele care indica masuri de sacouri sunt conventionale, astfel ca ele puteau fi inlocuite, de pilda, cu litere.

4 DISTRIBUTII SIMETRICE SI DISTRIBUTII ASIMETRICE

Dupa cum am aratat, daca lucram cu date nominale, singura marime a tendintei centrale pe care o putem folosi este modul, daca datele sunt ordinale, putem folosi atat modul, cat si mediana, iar daca datele sunt de interval sau de raport, putem folosi toate cele trei marimi ale tendintei centrale.

Dupa cum vom vedea in capitolele dedicate statisticii inferentiale, la nivel de interval sau de raport media aritmetica este cu deosebire utila pentru trage concluzii despre caracteristicile unei populatii pe baza caracteristicilor corespunzatoare ale unui esantion din acea populatie. Pentru scopuri descriptive insa, daca lucram cu date de interval sau de raport, este recomandabil sa folosim toate marimile tendintei centrale, deoarece, pe de o parte, ele pot furniza informatii relativ diferite si, pe de alta parte, compararea valorilor mediei aritmetice si medianei furnizeaza informatie despre forma unei distributii. Astfel, media aritmetica si mediana au aceeasi valoare numai atunci cand distributia este simetrica. Intr-un astfel de caz, daca distributia este unimodala, atunci si modul are aceeasi valoare cu celelalte doua marimi. Sa consideram urmatorul poligon de frecvente "rotunjit", care prezinta o distributie de frecvente simetrica:

Figura 3.1 O distributie simetrica (=)

,

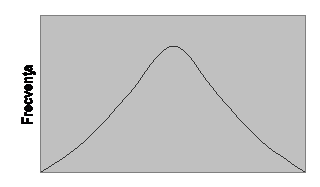
In aceasta distributie, media aritmetica, mediana si modul apar impreuna in cel mai inalt punct al curbei. Acest punct este modul, deoarece este punctul in care sunt inregistrate cele mai multe cazuri, este mediana, deoarece numarul de cazuri inregistrate la stanga acestui punct este egal cu numarul de cazuri inregistrat la dreapta sa si este media aritmetica, deoarece scorurile aflate in partea dreapta intrec scorul median in aceeasi masura in care scorurile aflate in partea stanga sunt mai mici decat scorul median.

Atunci cand o distributie are doar cateva scoruri foarte mari sau, altfel spus, scorurile relativ mici sunt predominante, media aritmetica este mai mare decat mediana. Intr-un astfel de caz, se spune ca distributia respectiva prezinta o asimetrie pozitiva. Figura 3.2 ilustreaza cazul unei distributii cu asimetrie pozitiva.

Figura 3.2 O distributie cu asimetrie pozitiva (>)

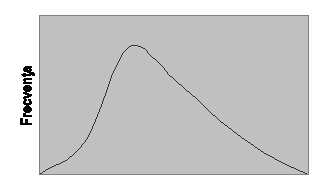
Atunci cand o distributie are doar cateva scoruri foarte mici sau, altfel spus, scorurile relativ mari sunt predominante, media aritmetica este mai mica decat mediana. Intr-un astfel de caz, se spune ca distributia respectiva prezinta o asimetrie negativa. Figura 3.3 ilustreaza cazul unei distributii cu asimetrie negativa.

Figura 3.3 O distributie cu asimetrie negativa (< )

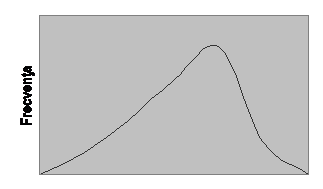
Dupa cum se poate constata, compararea mediei aritmetice cu mediana ne indica imediat daca distributia respectiva este sau nu simetrica si daca nu, ne indica sensul asimetriei.

5 MEDIA ARITMETICA PONDERATA

Sa presupunem ca intr-o serie de 140 de studenti sunt 86 de baieti si 54 de fete. Stim ca la examenul de statistica, media aritmetica a notelor obtinute de fete este 8,45 si media aritmetica a notelor obtinute de baieti este 7,33. Ne intereseaza media aritmetica a celor doua grupuri combinate. Daca am calcula pur si simplu media aritmetica a celor doua medii, am gresi, deoarece grupurile difera in privinta numarului de studenti si deci de scoruri. Pentru a afla media aritmetica a celor doua grupuri combinate, vom calcula media aritmetica ponderata. Pentru aceasta, inmultim numarul de scoruri din fiecare grup cu media aritmetica a grupului respectiv, adunam produsele astfel obtinute, iar rezultatul il impartim la numarul total de scoruri. In simboluri:

Formula 3.2

in care n_i = numarul de scoruri din fiecare grup

= media aritmetica a fiecarui grup

N = numarul total de scoruri

In exemplul nostru avem:

= = = 7,76

Daca am fi facut media aritmetica a valorilor 7,33 si 8,45 am fi obtinut 7,89, ceea ce ar fi fost incorect, caci grupurile difera in privinta numarului de scoruri. Evident, media aritmetica ponderata poate fi calculata si pentru mai mult de doua grupuri.

Este important de remarcat ca, aplicate la aceeasi multime de scoruri, formulele 3.1 si 3.2 produc acelasi rezultat. Pentru ilustrare, fie urmatoarea multime de 10 scoruri, impartita in doua grupuri: n₁ = , n₂ = . Media aritmetica pentru intreaga multime este

= = = = 6,90

Acum, mediile aritmetice ale celor doua grupuri sunt, respectiv, = 5,83 si = 8,50, astfel ca media aritmetica ponderata a celor doua grupuri este

= = = = 6,90

Inca odata, calculul mediei aritmetice a celor doua medii conduce la un rezultat gresit: 7,16.

6 MARIMILE TENDINTEI CENTRALE PENTRU DATE GRUPATE

In cele ce urmeaza sunt expuse tehnicile statistice de aflare a marimilor tendintei centrale pentru date de interval sau de raport grupate in distributii de frecvente. Aceste tehnici isi dovedesc utilitatea in doua situatii. O prima situatie apare atunci cand trebuie sa lucram cu o multime mare de scoruri brute si nu dispunem de un calculator sau de un computer sau decidem ca valorile aproximative ale acestor marimi sunt suficiente pentru scopurile noastre. O a doua situatie apare atunci cand avem de-a face cu date din surse secundare, deja organizate in distributii de frecvente cu intervale de clasa, fara sa avem acces la scorurile brute initiale. Intr-o astfel de situatie, intrucat nu cunoastem modul in care scorurile sunt realmente distribuite, nu putem decat sa aproximam marimile tendintei centrale ale distributiilor respective.

Pentru ilustrare, sa consideram exemplul privind scorurile obtinute de 180 de subiecti la un test de cunostinte, pe care am lucrat in capitolul anterior. Inainte de a trece mai departe, prezentam valorile calculate pentru scorurile brute, pentru a le putea compara cu cele calculate pentru datele grupate. Astfel, in exemplul nostru avem:

= 49,22 = 49 Mo = 56

Sa consideram acum distributia de frecvente a scorurilor obtinute de 180 de subiecti la un teste de cunostinte:

Tabelul 3.6 Distributia de frecvente a scorurilor

obtinute la un test de cunostinte

Media aritmetica pentru date grupate

Pentru a calcula media aritmetica a unei multimi de scoruri trebuie sa cunoastem doua valori: suma tuturor scorurilor, ΣX_i, si numarul de scoruri, n. In cazul distributiei din tabelul 3.6, nu stim decat ca n = 180. Deoarece datele au fost grupate, nu cunoastem distributia exacta a scorurilor individuale si deci nu putem determina exact ΣX_i.

Sa consideram primul interval (20-24). In acest interval se afla un singur caz, dar nu stim care este scorul acestuia. Pentru a depasi aceasta lacuna, vom presupune ca scorul acestui caz este situat in centrul intervalului. Aceasta presupunere revine la a spune ca scorul cazului din acest interval este 22, acest numar aproximand scorul sau efectiv. In cel de-al doilea interval (25-29) se afla doua cazuri. Si aici vom presupune ca scorurile celor doua cazuri sunt situate in centrul intervalului, presupunere care revine la a spune ca fiecare dintre cele doua cazuri are scorul 27. Sub aceasta presupunere, suma scorurilor individuale din cel de-al doilea interval este 54 (27 2), acest numar aproximand suma reala a scorurilor individuale din interval. Procedand la fel pentru celelalte intervale si adunand apoi rezultatele, vom obtine un numar care aproximeaza suma reala a tuturor scorurilor individuale. In fine, impartind valoarea astfel obtinuta la numarul de scoruri (180), vom obtine media aritmetica aproximativa a scorurilor.

In general, supozitia calculului mediei aritmetice pentru date grupate este ca in fiecare interval de clasa, toate scorurile sunt situate in centrul intervalului respectiv. Sub aceasta supozitie, procedura de calcul este urmatoarea:

1.     Pentru fiecare interval i, se calculeaza centrul m_i.

2.     Numarul de cazuri din fiecare interval, f_i, se inmulteste cu centrul intervalului respectiv, m_i: f_im_i.

3.     Se calculeaza Σf_im_i, iar valoarea astfel obtinuta se imparte la numarul de scoruri n.

Intrucat Σf_im_i ΣX_i, vom avea:

Formula 3.3

Pentru a aplica aceasta procedura la exemplul nostru, vom adauga doua coloane la distributia de frecvente din tabelul 3.6, una pentru centrele de interval si una pentru produsele dintre centrele de interval si frecvente:

Tabelul 3.7 Calculul mediei aritmetice

pentru date grupate

Totalul ultimei coloane este valoarea pentru Σf_im_i. Impartind aceasta valoare la numarul total de cazuri obtinem media aritmetica aproximativa a scorurilor:

= = 49,25

Dupa cum se poate constata, valoarea obtinuta in acest fel reprezinta o deosebit de buna aproximare a valorii efective a mediei aritmetice.

Mediana pentru date grupate

Stim ca pentru a afla mediana unei distributii ordonate de scoruri trebuie sa identificam mai intai cazul sau cazurile de mijloc al distributiei respective. Atunci cand se lucreaza cu date grupate, se introduce o simplificare: cazul de mijloc este identificat la n 2, indiferent daca n este par sau impar. In exemplul nostru, avand 180 de cazuri in esantion, cazul de mijloc va fi identificat la 180 2, i.e. al 90-lea caz. Mai departe, problema este de a localiza acest caz si apoi de a afla scorul asociat lui. Evident, atunci cand datele sunt grupate, cazul de mijloc se afla intr-un interval de clasa. Supozitia calculului medianei pentru date grupate este ca in fiecare interval de clasa, toate scorurile sunt distribuite uniform intre limitele reale ale intervalului. Astfel, dupa ce identificam intervalul care contine cazul de mijloc, vom afla scorul respectiv pe baza acestei supozitii. Pentru identificarea intervalului de clasa care contine cazul de mijloc, adaugam o coloana de frecvente cumulate la distributia de frecvente initiala:

Tabelul 3.8 Calculul medianei

pentru date grupate

Inspectand coloana de frecvente cumulate, constatam ca 50 de cazuri s-au cumulat sub limita superioara a intervalului 40-44 si ca 92 de cazuri s-au cumulat sub limita superioara a intervalului 45-49. Stim acum ca mediana - scorul asociat celui de-al 90-lea caz - este o valoare cuprinsa intre limita reala inferioara si limita reala superioara ale intervalului 45-49, adica intre 44,5 si 49,5. Mai departe, presupunem ca toate cele 42 de cazuri situate in acest interval sunt distribuite uniform intre limitele reale ale intervalului, cazul 51 fiind situat la limita reala inferioara (44,5), iar cazul 92 la limita reala superioara (49,5). In intervalul care contine mediana sunt 42 de cazuri, cazul 92, cumulat in acest interval, fiind al 42-lea; prin urmare, cazul 90 este al 40-lea din cele 42 din interval[4]. Aceasta revine la a spune ca, pentru a afla al catelea caz este cazul 90, scadem din 90 frecventa cumulata a cazurilor aflate sub intervalul in care se afla mediana: 90 - 50 = 40. Daca, asa cum am presupus, scorurile sunt distribuite uniform, atunci cazul 90 se afla la 40 42 din distanta dintre 44,5 si 49,5. Acum, 40 42 din 5 (marimea intervalului) este 4,76, astfel incat putem aproxima mediana la 44,5 + 4,76 sau 49,26.

In general, sub supozitia ca in fiecare interval de clasa toate scorurile sunt distribuite uniform intre limitele reale ale intervalului, procedura de calcul a medianei pentru date grupate este urmatoarea:

1.     Se afla cazul de mijloc, dat de n/2.

2.     Se construieste o coloana de frecvente cumulate si cu ajutorul acesteia se identifica intervalul care contine cazul de mijloc.

3.     Se afla al catelea caz din interval este cazul de mijloc, scazand din n/2 frecventa cumulata a cazurilor aflate sub intervalul identificat in pasul2.

4.     Numarul obtinut in pasul 3 se imparte la numarul de cazuri din interval.

5.     Numarul obtinut in pasul 4 se inmulteste cu marimea intervalului.

6.     Numarul obtinut in pasul 5 se aduna cu limita de clasa reala inferioara a intervalului care contine cazul de mijloc. Rezultatul reprezinta valoarea aproximativa a medianei.

Formula urmatoare rezuma acesti pasi:

Formula 3.4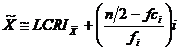

in care = limita de clasa reala inferioara a intervalului care contine al n 2-lea caz

n = numarul total de cazuri

fc_i = frecventa cumulata sub intervalul care contine al n 2-lea caz

f_i = numarul de cazuri din intervalul care contine al n 2-lea caz

i = marimea intervalului care contine al n 2-lea caz

Aplicand aceasta formula la exemplul nostru, avem:

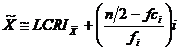= = 44,5 + 4,76 = 49,26

Vom spune ca aproximativ jumatate din subiectii din esantion au obtinut un scor mai mic de 49,26 si jumatate mai mare de 49,26. Si de data aceasta se poate constata ca valoarea obtinuta in acest fel reprezinta o foarte buna aproximare a valorii efective a medianei.

Intervalul modal

Atunci cand datele sunt grupate, scorul modal efectiv al distributiei de frecvente respective nu poate fi determinat. Intr-o astfel de situatie se poate determina doar intervalul modal - intervalul care contine cel mai mare numar de cazuri -, centrul acestui interval fiind considerat modul distributiei. Pentru o mai buna aproximare a modului unei distributii cu date grupate, in cazul in care distributia are doua sau mai multe intervale neadiacente in care numarul de scoruri este mai mare decat in intervalele adiacente, atunci distributia respectiva este considerata multimodala (bimodala, trimodala etc.). In exemplul nostru, conform definitiei stricte, intervalul modal este 45-49, astfel ca centrul acestui interval, 47, apare ca mod al distributiei. Totusi, intrucat aici apar doua intervale neadiacente, 45-49 si 55-59, in care numarul de scoruri este mai mare decat in intervalele adiacente, 42 si respectiv 37, vom considera ca distributia este bimodala, cele doua moduri fiind centrele de interval respective: 47 si 57. Se poate constata ca intervalul 55-59 contine modul efectiv al distributiei de frecvente, 56.