PREZENTAREA DATELOR STATISTICE - PSIHOLOGIE

Functia de baza a statisticii descriptive este prezentarea clara si concisa a rezultatelor cercetarii. In acest capitol sunt expuse o serie de tehnici de organizare si prezentare rezumativa a datelor: procente, proportii, raporturi, rate, distributii de frecvente, diagrame si grafice.

1 PROCENTE SI PROPORTII

Imaginati-va ca sunteti seful unui departament al unei mari companii de asigurari si ca, dorind sa prezentati directorului executiv al companiei o problema de personal cu care va confruntati, ii spuneti urmatoarele: "Oamenii din departamentul meu nu sunt suficient de bine platiti. Desi din cei 154 de angajati permanenti ai companiei numai 37 sunt in departamentul meu, din cele 17832 de contracte de asigurare incheiate in companie anul trecut, 7321 au fost aduse de angajatii din departamentul pe care il conduc". Probabil ca dupa o astfel de prezentare, directorul executiv ar schita o grimasa de plictiseala si ar amana elegant discutia pentru o data neprecizata. Intrucat este vorba de compararea a cate doua numere (personalul departamentului fata de numarul total de angajati ai companiei si volumul de munca din departament fata de volumul total de munca din companie pe timp de un an), procentele si proportiile ar fi fost modalitati mai convingatoare de prezentare a informatiei.

Definitiile matematice ale proportiei si procentului sunt urmatoarele:

Formula 1 Proportie () =

Formula 2 Procent (%) =

in care = frecventa sau numarul de cazuri in fiecare categorie

n = numarul total de cazuri (numarul de cazuri din toate categoriile)

Urmatorul tabel ilustreaza calcularea proportiilor si procentelor:

Tabelul 1 Opinia fata de interzicerea fumatului

in locurile publice (date fictive)

Pentru a afla proportia cazurilor din prima categorie (De acord cu interzicerea fumatului in locurile publice), notam ca avem aici 167 de cazuri (= 167) fata de 269 de cazuri in esantion (n = 269). Astfel:

Proportie () = = = 0, 621

Procedand la fel, aflam proportiile cazurilor din celelalte categorii. Rezultatele pot fi exprimate sub forma de procente. Astfel, procentul de cazuri din cea de-a treia categorie (Nu stiu/Nu raspund) este

Procent (%) = = = 11,1%

Exprimarea rezultatelor prin procente si proportii este cu deosebire utila atunci cand dorim sa comparam grupuri de marimi diferite. Sa presupunem, de pilda, ca am adunat urmatoarele date privind doua universitati:

Tabelul 2 Numarul de studenti inscrisi pe specializari

la doua universitati (date fictive)

Intrucat numarul total de studenti inscrisi difera mult de la o universitate la alta, compararea numarului relativ de studenti inscrisi pe specializari la cele doua universitati este greu de facut numai pe baza frecventelor. Care universitate, de pilda, are cel mai mare numar relativ de studenti inscrisi la specializarea Psihologie? Pentru a inlesni comparatiile de acest fel, calculam procentele de studenti inscrisi pe specializari la cele doua universitati:

Tabelul 3 Procentul de studenti inscrisi pe specializari

la doua universitati (date fictive)

Procentele prezentate in acest tabel permit identificarea atat a diferentelor, cat si a asemanarilor dintre cele doua universitati. De pilda, Universitatea A are un procent mai mare de studenti inscrisi la specializarea Psihologie, desi numarul absolut de studenti inscrisi la acest profil este mai mic decat la Universitatea B, iar la specializarea Sociologie, procentele sunt aproape aceleasi.

Remarcati ca sub fiecare coloana de procente am mentionat totalul in date absolute sau, altfel spus, am mentionat dimensiunea esantionului. In general, daca nu se mentioneaza baza de comparatie, atunci procentele si proportiile nu ne spun nimic sau chiar ne pot induce in eroare. Sa presupunem, de pilda, ca o firma care produce bauturi racoritoare anunta ca ultimul sau produs are cu 20% mai putine calorii. Problema este: 20% mai putin fata de ce? Fara mentionarea bazei de comparatie, pretentia firmei respective este lipsita de sens. Unele reclame impresioneaza prin prezentarea unor proportii, cum ar fi "Doua din trei persoane prefera marca X de produs marcii Y". Ce ati gandi despre o astfel de reclama, daca ati afla ca, de fapt, au fost chestionate doar trei persoane? Cunostintele de statistica isi dovedesc utilitatea si in mai buna intelegere si evaluare a informatiilor "statistice" prezentate in presa scrisa sau pe posturile de radio si televiziune.

O eroare care poate sa apara in folosirea procentelor consta din incercarea de a aduna procentele ca si cum ar fi numere cardinale. Sa presupunem de pilda, ca producatorul national de energie electrica anunta cresterea pretului pe kilowatt cu 50%. Pentru "justificarea" acestei cresteri, producatorul arata ca au crescut costurile de productie a energiei electrice, dupa cum urmeaza: pretul combustibilului folosit in termocentrale cu 10%, costurile investitiilor in retehnologizare cu 20% si cheltuielile cu forta de munca cu 10%, in total, o crestere a costurilor cu 50%. O astfel de justificare este gresita. Doar o crestere cu 50% a tuturor costurilor ar justifica o crestere cu 50% a pretului pe kilowatt.

Revenind la exemplul dat la inceputul aceste sectiuni, informatia prezentata directorului executiv al companiei ar fi fost mai convingatoare daca i-ati fi spus: "Desi in departamentul meu lucreaza doar 24% din angajatii companiei, oamenii mei au adus 41% din contractele de asigurare incheiate anul trecut in companie".

2 RAPORTURI SI RATE

Sa consideram din nou tabelul Cat de multi studenti sunt inscrisi la Stiinte economice in comparatie cu cei inscrisi la Psihologie in Universitatea B? Putem folosi frecventele pentru a raspunde la aceasta intrebare, dar un raspuns mai usor de inteles poate fi dat folosind un raport. Raporturile se calculeaza impartind frecventa cazurilor dintr-o categorie la frecventa cazurilor din alta categorie, permitand astfel compararea categoriilor in termeni de frecventa relativa. Definitia matematica a raportului este urmatoarea:

Formula 3                Raport =

in care = numarul de cazuri din categoria i

= numarul de cazuri din categoria j

Raportul ne spune exact in ce masura categoria i depaseste in numar de cazuri categoria j. In exemplul nostru, raportul studentilor inscrisi la Stiinte Economice fata de cei inscrisi la Psihologie in Universitatea B este:

Raport = = = 1,48

Aceasta inseamna ca pentru fiecare student inscris la Psihologie exista 1,48 studenti inscrisi la Stiinte Economice.

Raporturile pot fi multiplicate cu 100 pentru a elimina virgulele. Astfel, raportul calculat mai sus poate fi prezentat ca 148, ceea ce inseamna ca pentru fiecare 100 de studenti inscrisi la psihologie exista 148 de studenti inscrisi la Stiinte Economice.

Ratele se calculeaza impartind numarul de cazuri reale (efective) la numarul de cazuri posibile pentru variabila de interes pe o anumita unitate de timp. De pilda, rata bruta a natalitatii pentru o populatie se calculeaza impartind numarul de nascuti vii la numarul total de persoane din acea populatie pe an, catul astfel obtinut fiind inmultit cu 1000. Se spune ca rezultatul este exprimat in promile (⁰/₀₀). Daca, de pilda, intr-un oras cu 7000 de locuitori s-au inregistrat intr-un anumit an 100 de nascuti vii, rata bruta a natalitatii este

Rata bruta a natalitatii (⁰/₀₀) = ⁰/₀₀

Aceasta inseamna ca pentru fiecare mie de locuitori au fost in acel an 14,3 nascuti vii.

Ca modalitati de a exprima frecvente relative, procentele, proportiile, raporturile si ratele sunt utile in special atunci cand dorim sa comparam diferite grupuri sau/si acelasi grup in momente diferite.

3 DISTRIBUTII DE FRECVENTE

O distributie de frecvente este o dispunere a valorilor unei variabile care arata cate cazuri sunt continute in fiecare categorie a variabilei respective. Construirea unei distributii de frecvente este, de regula, primul pas in orice analiza statistica. Sa presupunem ca urmatoarele date reprezinta scorurile obtinute de 180 de subiecti la un test de cunostinte:

Tabelul 4 Scoruri obtinute la un test de cunostinte

Datele brute din tabelul 4 sunt greu de urmarit si greu de inteles. Sub supozitia ca este vorba despre date de interval, putem construi o distributie de frecvente listand scorurile diferite in ordine crescatoare si inregistrand frecventa de aparitie a fiecarui scor. Distributia de frecvente astfel obtinuta este urmatoarea:

Tabelul 5 Distributia de frecvente a scorurilor

obtinute la un test de cunostinte

De notat ca aceasta distributie de frecvente reda si informatia conform careia in esantionul considerat nu au fost obtinute scorurile 26, 27, 28, 31 si 66, aflate intre cel mai mic scor si cel mai mare scor.

In distributia de frecvente din tabelul 5 am inclus toate scorurile diferite cuprinse intre cel mai mic scor si cel mai mare scor. Cu alte cuvinte, am clasificat datele intr-un numar de grupuri sau clase egal cu numarul de scoruri distincte. Dupa cum arata si acest exemplu, construirea unei distributii in acest fel are drept rezultat o lista destul de lunga si nu tocmai clarificatoare. Atunci cand numarul de scoruri distincte este mare, se opteaza pentru o prezentare mai compacta (mai putin detaliata) a datelor, prin gruparea acestora in categorii mai largi, care, in cazul datelor de interval sau de raport, se numesc intervale de clasa. In tabelul 6 se prezinta o distributie de frecvente pentru datele din tabelul 4, in care apar 10 intervale de clasa, marimea fiecarui interval fiind egala cu 5 unitati. Adaugand si o coloana de procente pentru scorurile din fiecare categorie fata de numarul total de scoruri vom spori claritatea prezentarii.

Tabelul 6 Distributia de frecvente a scorurilor

obtinute la un test de cunostinte

(marimea intervalului = 5)

Distributia de frecvente din tabelul 6 evidentiaza predominanta relativa a scorurilor din intervalele 45-49 (23,33%) si 55-59 (20,56%). Pe de alta parte, gruparea scorurilor in acest tabel conduce la o pierdere de informatie fata de prezentarea din tabelul 5. Nu stim, de pilda, cati subiecti au obtinut, respectiv, scorurile 35, 36, 37, 38 si 39, ci doar ca sunt 18 scoruri in intervalul 35-39. Apoi, din tabelul 6 nu reiese ca in esantionul considerat nu au fost obtinute scorurile 26, 27, 28, 31 si 66. Sa mai notam ca, la rigoare, se poate spune ca in distributia de frecvente din tabelul 5, marimea fiecarui interval este egala cu o unitate.

In general, regulile de construire a unei distributii de frecvente pentru date de interval sau de raport in care se utilizeaza intervale de clasa de marime diferita fata de datele initiale sunt urmatoarele:

1.     Se decide asupra numarului de intervale de clasa care vor fi utilizate. Numarul de intervale de clasa nu trebuie sa fie atat de mare incat sa nu permita sesizarea predominantei relative a anumitor grupari de scoruri, dar nici atat de mic incat sa conduca la pierderea unor informatii semnificative. De regula, se utilizeaza intre 5 si 20 de intervale, in functie de numarul de scoruri din multimea initiala de date si de scopurile cercetarii.

2.     In functie de numarul de intervale de clasa ales, se stabileste marimea intervalelor de clasa. In mod obisnuit, pentru a se inlesni interpretarea distributiei de frecvente, se folosesc intervale de clasa de aceeasi marime. Marimea unui interval de clasa se stabileste impartind diferenta dintre cel mai mare scor si cel mai mic scor din multimea scorurilor date, numita amplitudine a multimii respective[1], la numarul intervalelor de clasa si rotunjind rezultatul pana la un numar intreg convenabil.

3.     Se stabileste primul interval astfel incat sa contina cel mai mic scor (limita sa inferioara sa fie mai mica sau egala cu cel mai mic scor). Ultimul interval va fi acela care contine cel mai mare scor. Intervalele nu trebuie sa se suprapuna.

4.     Se numara scorurile din fiecare interval de clasa si se inregistreaza rezultatele intr-o coloana etichetata ("frecventa"). La sfarsitul acestei coloane se prezinta numarul total de scoruri. Pentru mai multa claritate, se poate adauga o coloana de procente.

Sa vedem cum au fost aplicate aceste reguli pentru construirea distributiei de frecvente din tabelul 6. Scorul cel mai mare si scorul cel mai mic fiind, respectiv, 69 si 24, amplitudinea scorurilor este 69 - 24 = 45. Alegand un numar de 10 intervale de clasa, marimea fiecarui interval de clasa este 45 10 = 4,5 5. Primul interval, care trebuie sa includa cel mai mic scor, poate fi oricare dintre urmatoarele:

20-24, 21-25, 22-26, 23-27, 24-28

Fiecare dintre aceste intervale contine cinci scoruri[2], inclusiv scorul 24, deci poate fi ales. In exemplul nostru am ales intervalul 20-24. Ca atare, urmatorul interval este 25-29 s.a.m.d. pana la ultimul interval, 65-69, care contine cel mai mare scor. De notat ca intervalele din tabelul 24 par a nu fi reciproc exclusive. In realitate lucrurile nu stau asa. Daca, dupa intervalul 20-24 ar fi urmat 24-28, 28-32 s.a.m.d., am fi obtinut intervale suprapuse doua cate doua. Scorul 24, de pilda, ar fi facut parte atat din intervalul 20-24, cat si din intervalul 24-28. Intervalele de clasa din tabelul 6 sunt exhaustive (acopera toate scorurile din multimea initiala de scoruri) si reciproc exclusive (fiecare scor face parte dintr-un singur interval).

Distributiile de frecvente pentru date de interval sau de raport pot contine doua instrumente ajutatoare in prezentarea datelor: frecvente cumulate si procente cumulate. Frecventele cumulate prezinta numarul de cazuri dintr-un interval de clasa si din toate intervalele de clasa precedente, iar procentele cumulate prezinta procentul de cazuri dintr-un interval de clasa si din toate intervalele precedente[3]. Tabelul urmator prezinta o coloana de frecvente cumulate si o coloana de procente cumulate pentru distributia de frecvente din tabelul 6.

Tabelul 7 Distributia de frecvente a scorurilor

obtinute la un test de cunostinte

Pentru a construi distributia de frecvente cumulate din tabelul 7 incepem cu primul interval de clasa, 20-24. Pentru acest interval, intrarea in coloana de frecvente cumulate este identica cu numarul de scoruri din interval, 1. Pentru intervalul imediat urmator, 25-29, se aduna numarul de scoruri din interval, 2, cu numarul de scoruri din primul interval, 1, obtinandu-se frecventa cumulata a intervalului, 3. Se procedeaza la fel pentru fiecare interval, adunand frecventa din intervalul respectiv cu frecventa cumulata in intervalul imediat anterior. Evident, frecventa cumulata in ultimul interval de clasa este egala cu numarul total de scoruri.

Construirea coloanei de procente cumulate urmeaza acelasi model aditiv cu cel folosit pentru frecvente cumulate. Astfel, pentru primul interval, intrarea in coloana de procente cumulate este identica cu procentul din interval. Pentru intervalul imediat urmator, procentul cumulat este procentul scorurilor din interval plus procentul scorurilor din primul interval s.a.m.d. pana la ultimul interval, in care, evident, procentul cumulat este egal cu 100%. De notat ca aceleasi rezultate se obtin prin aplicarea formulei 2, in care se inlocuieste cu pentru fiecare interval de clasa, n fiind numarul total de scoruri.

Frecventele si procentele cumulate arata felul in care sunt distribuite cazurile in plaja de scoruri. De pilda, tabelul 7 arata ca o majoritate semnificativa de subiecti din esantion - 122, respectiv 67,78% - au obtinut scoruri mai mici de 55.

Pana acum am considerat scorurile inregistrate la testul de cunostinte ca fiind date discrete. Masurarea unei variabile produce date discrete, daca inregistrarea acestora se face in categorii reciproc exclusive (nesuprapuse). Pentru anumite scopuri[4], distributia unei variabile masurabila la nivel de interval sau de raport trebuie construita ca o serie continua de categorii partial suprapuse. Pentru a obtine o distributie continua de scoruri ale unei astfel de variabile, se porneste de la limitele intervalele de clasa stabilite initial, numite limite stabilite si, pe baza acestora, se determina asa-numitele limite reale sau exacte. Pentru determinarea acestor limite, se imparte la doi "distanta" aritmetica dintre intervalele de clasa stabilite initial, iar rezultatul astfel obtinut se scade din fiecare limita inferioara stabilita si se aduna la fiecare limita superioara stabilita. Tabelul 8 prezinta rezultatele aplicarii aceste proceduri la intervalele de clasa stabilite in tabelul 6. Intrucat "distanta" aritmetica dintre intervalele de clasa din tabelul 4 este de o unitate, limitele reale se afla scazand 0,5 din fiecare limita inferioara si adunand 0,5 la fiecare limita superioara. In tabelul 8 este adaugata o coloana etichetata centre de interval. Centrele de interval sunt punctele situate exact la mijlocul unui interval si se afla impartind la doi suma limitelor inferioara si superioara ale intervalului[5]. De notat ca centrele de interval sunt aceleasi, indiferent daca folosim limite stabilite sau limite reale.

Tabelul 8 Distributia de frecvente a scorurilor

obtinute la un test de cunostinte (incluzand

limite reale si centre de interval)

Se poate observa ca intervalele de clasa cu limite reale se suprapun partial doua cate doua, astfel ca distributia apare ca fiind continua.

Distributiile de frecvente se pot construi si pentru variabile masurate la nivelele nominal sau ordinal. Pentru fiecare categorie a variabilei respective se numara cazurile si se prezinta subtotalurile, precum si numarul total de cazuri (n). Sa presupunem, de pilda, ca suntem interesati de masurarea variabilei nivel de scolarizare pentru cei 180 de subiecti care au raspuns la un test de cunostinte si ca decidem sa folosim urmatoarea scala ordinala de masura: 1. nu a absolvit nici o scoala; a absolvit cel mult ciclul obligatoriu de invatamant; 3. a absolvit cel mult liceul; 4. a absolvit cel mult cursuri postliceale, neuniversitare; 5. a absolvit cel mult cursuri universitare; 6. a absolvit cursuri post universitare. Folosind numerele de ordine ale categoriilor drept coduri (etichete), tabelul 9 ilustreaza construirea unei distributii de frecvente pentru variabila mentionata.

Tabelul 9 Nivelul de scolarizare

pentru cei 180 de subiecti

Adaugarea unei coloane de procente pentru categorii aduce un spor de claritate a prezentarii. De notat ca la nivelele nominal si ordinal, frecventele cumulate si procentele cumulate sunt lipsite de sens. De asemenea, intrucat la aceste nivele categoriile sunt intotdeauna discrete, nu are sens sa se determine limitele de clasa reale si centrele de interval. Singura coloana care poate fi adaugata la distributiile de frecvente pentru variabile la orice nivel de masura este coloana de procente.

4 DIAGRAME SI GRAFICE

Diagramele si graficele sunt modalitati de prezentare vizuala a datelor statistice si furnizeaza o imagine globala a formei unei distributii. Alegerea unei modalitati sau a alteia depinde, in principal, de nivelul de masura folosit si de scopurile cercetarii.

Diagrame circulare

O diagrama circulara este pur si simplu un cerc impartit intr-un numar de sectoare egal cu numarul de categorii ale variabilei de interes, marimea fiecarui sector fiind proportionala cu procentajul de cazuri din categoria respectiva. Diagramele circulare pot fi folosite pentru variabile masurate la nivelele nominal si ordinal.

Sa presupunem ca am inregistrat statusul marital al celor 180 de subiecti care au raspuns la un test de cunostinte si ca am obtinut urmatoarele date:

Tabelul 10 Statusul marital pentru cei 180 de subiecti

^TPersoana care nu a fost niciodata casatorita

Sa construim o diagrama circulara pentru datele din acest tabel. Intrucat circumferinta unui cerc are 360⁰, vom aloca 126⁰ (35% din 360⁰) pentru prima categorie, 180⁰ (50% din 360⁰) pentru cea de-a doua categorie si 54⁰ (15 % din 360⁰) pentru cea de-a treia categorie. Obtinem urmatoarea diagrama circulara:

Figura 1 Statusul marital al celor 180 de subiecti

Diagrama din figura 1 evidentiaza vizual preponderenta relativa a subiectilor casatoriti si lipsa relativa a subiectilor divortati din esantionul considerat.

Diagrame cu coloane si diagrame cu linii

Diagramele cu coloane reprezinta o alta modalitate de prezentare vizuala a datelor statistice. Ca si diagramele circulare, diagramele cu coloane pot fi folosite pentru variabile masurate la nivelele nominal si ordinal. Intr-o astfel de diagrama, categoriile variabilei de interes apar pe o axa orizontala (axa absciselor), iar frecventele (relative) apar pe axa verticala corespunzatoare (axa ordonatelor). Pe axa orizontala se construiesc atatea coloane (dreptunghiuri) cu baze egale cate categorii sunt de prezentat. Inaltimea unei coloane este proportionala cu frecventa (relativa) a cazurilor din categoria respectiva. Intrucat la nivelele nominal si ordinal categoriile variabilelor sunt discrete, coloanele sunt separate intre ele de o distanta egala, de regula, cu ½ din latimea lor.

Diagrama cu coloane din figura 2 prezinta in procente fata de total statusul marital al subiectilor din tabelul 9.

Figura 2 Statusul marital al celor 180 de subiecti

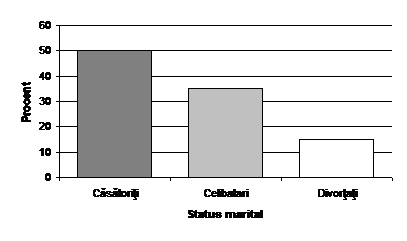
Decizia de a utiliza o diagrama circulara sau o diagrama cu coloane depinde de numarul de categorii ale variabilei de interes si de scopul cercetarii. Daca o variabila are mai mult de sase sau sapte categorii, atunci este preferabila o diagrama cu coloane, caci o diagrama circulara cu prea multe categorii devine prea aglomerata si deci greu de citit.

Diagramele cu coloane sunt utile in special pentru a prezenta frecventele (relative) pentru doua sau mai multe categorii ale unei variabile, cu scopul de a face unele comparatii. Sa presupunem, de pilda, ca dorim sa facem o comparatie pe sexe a numarului de angajati ai unei firme care, in primele sase luni ale unui an, au apelat la serviciile centrului de consiliere psihologica al firmei. Figura 3 prezinta datele (fictive) obtinute.

Figura 3 Numarul de angajati care au apelat la serviciile

centrului de consiliere psihologica

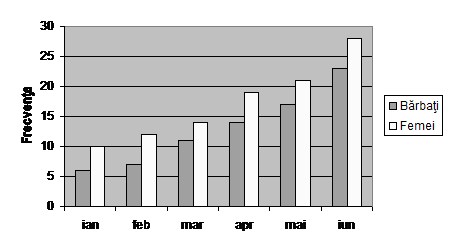
Aceasta diagrama arata ca, in timp ce numarul de angajati care au apelat la serviciile centrului de consiliere psihologica in perioada mentionata a fost in crestere, numarul de apelanti femei a crescut mai repede decat numarul de apelanti barbati. Aceeasi informatie este prezentata printr-o diagrama cu linii in figura 4.

Figura 4 Numarul de angajati care au apelat la serviciile

centrului de consiliere psihologica

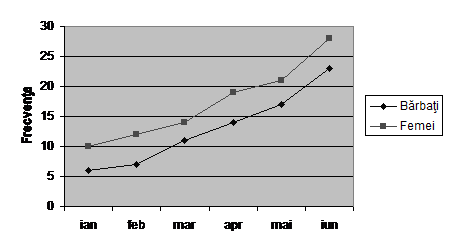
Ca si diagramele circulare si diagramele cu coloane, diagramele cu linii, indeobste cunoscute sub denumirea de "grafice", sunt larg folosite in mass-media pentru prezentarea diferitelor date statistice.

Histograme si poligoane de frecvente

Histogramele sunt modalitati de prezentare vizuala a distributiilor de frecvente pentru date de interval sau de raport, asemanatoare diagramelor cu coloane. Intrucat intr-o histograma se folosesc limitele de clasa reale ale intervalelor considerate, coloanele apar in contact doua cate doua. Figura 5 prezinta o histograma pentru datele din tabelul 7.

Figura 5 Histograma scorurilor obtinute

la un test de cunostinte

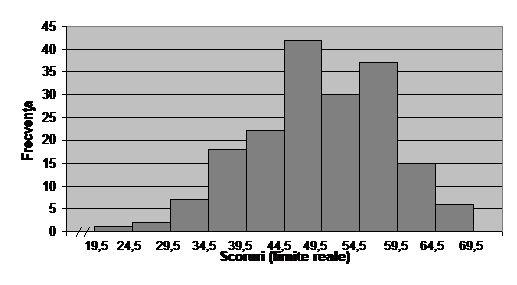
In general, o histograma se construieste dupa cum urmeaza:

1.     Intervalele de clasa sau scorurile se dispun pe axa orizontala (axa absciselor), utilizand limite de clasa reale.

2.     Frecventele se dispun pe axa verticala (axa ordonatelor).

3.     Se construieste cate o coloana pentru fiecare interval, cu inaltimea corespunzatoare numarului de cazuri din interval si cu latimea corespunzatoare limitelor reale ale intervalului.

4.     Se eticheteaza axele.

Alta modalitate obisnuita de prezentare vizuala a distributiilor de frecvente pentru variabile de interval sau de raport este poligonul de frecvente. Un poligon de frecvente utilizeaza centrele de interval si se construieste dupa cum urmeaza:

1.     Se plaseaza cate un punct in dreptul fiecarui centru de interval, la inaltimea corespunzatoare frecventei din intervalul respectiv.

2.     Punctele astfel obtinute se unesc prin linii drepte.

3.     Se inchide poligonul, considerandu-se cate un interval suplimentar cu frecventa zero la fiecare capat al distributiei si unind prin linii drepte punctele extreme cu centrele de interval (aflate pe abscisa) ale intervalelor suplimentare.

4.     Se eticheteaza axele.

Pentru simplificarea constructiei, pe axa absciselor se pot marca direct centrele de interval, in locul limitelor de clasa. Desi reda aceeasi informatie ca si histogramele, poligoanele de frecvente sunt utile pentru a da o imagine generala a unei distributii de frecvente.

Figura urmatoare prezinta un poligon de frecvente care reda aceeasi informatie ca si histograma din figura precedenta.

Figura 6 Poligonul de frecvente al scorurilor

obtinute la un test de cunostinte

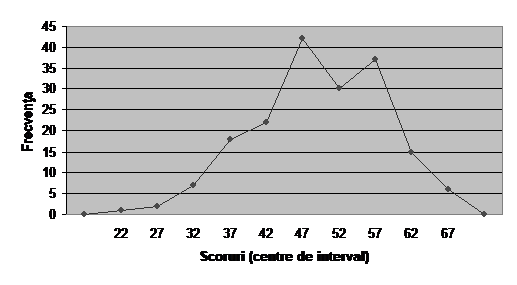
Ogive

Ogivele, numite si "curbe cumulative ale frecventelor" sau "poligoane de frecvente cumulate", prezinta vizual frecventele cumulate sau procentele cumulate ale unei distributii O ogiva utilizeaza limitele de clasa reale superioare ale intervalelor (LCRS) si se construieste dupa cum urmeaza:

1.     LCRS se dispun pe axa absciselor.

2.     Frecventele cumulate sau procentele cumulate se dispun pe axa ordonatelor.

3.     Se plaseaza cate un punct in dreptul fiecarei LCRS, la inaltimea corespunzatoare frecventei cumulate sau procentului cumulat in intervalul corespunzator acelei LCRS.

4.     Punctele astfel obtinute se unesc prin linii drepte.

5.     Ogiva se inchide la stanga, extinzand o linie dreapta catre limita de clasa reala inferioara a primului interval.

6.     Se eticheteaza axele.

Figura 7 prezinta o ogiva pentru datele din tabelul 6.

Figura 7 Ogiva pentru scorurile obtinute

la un test de cunostinte

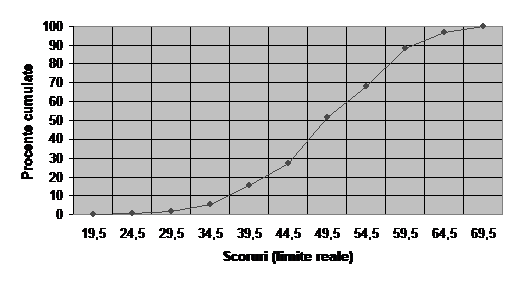
Dupa cum vom vedea in capitolul 3, o ogiva poate fi utilizata pentru a afla diferite puncte de interes intr-o distributie de frecvente.

In capitolul 11 vom folosi diagrame de imprastiere, numite si "diagrame ale norilor de puncte" sau "scatergrame[6]", care sunt modalitati de prezentare vizuala a corelatiei dintre doua variabile masurate la nivel de interval sau de raport.

GLOSAR

Centre de interval: puncte situate exact la mijlocul unui interval de clasa.

Diagrama circulara: cerc impartit intr-un numar de sectoare egal cu numarul de categorii ale variabilei de interes, marimea fiecarui sector fiind proportionala cu procentul de cazuri din categoria respectiva..

Diagrama cu coloane: modalitate de prezentare vizuala a distributiei unei variabile, in care categoriile sunt reprezentate prin coloane cu baza egala, inaltimea fiecarei coloane fiind proportionala cu procentul de cazuri din categoria respectiva.

Distributie de frecvente: dispunere a valorilor unei variabile, care arata cate cazuri sunt continute in fiecare categorie a variabilei respective.

Frecventa cumulata: numarul de cazuri dintr-un interval de clasa si din toate intervalele  precedente.

Histograma: modalitate de prezentare vizuala a distributiilor de frecvente pentru variabile de interval sau de raport, in care categoriile sunt reprezentate prin coloane continue cu baza egala cu limitele reale ale inervalelor de clasa respective, inatimea fiecarei coloane fiind proportionala cu procentul de cazuri din interval.

Intervale de clasa: categorii utilizate in cazul distributiilor de frecvente pentru variabile de interval sau de raport.

Limite de clasa reale: limitele superioara si inferioara ale intervalelor de clasa, folosite atunci cand distributia de frecvente respectiva este considerata ca fiint continua.

Limite stabilite: limitele superioara si inferioara ale intervalelor de clasa,  asa cum apar acestea in distributia de frecvente initiala.

Ogiva: modalitate de  prezentare vizuala a frecventelor cumulate sau a procentelor cumulate ale unei distributii de frecvente pentru variabile de interval sau de raport.

Procent: numarul de cazuri dintr-o categorie a unei variabile impartit la numarul de cazuri din toate categoriile variabilei respective, rezultatul fiind inmultit cu 100.

Procent cumulat procentul de cazuri dintr-un interval de clasa si din toate intervalele precedente.

Proportie: numarul de cazuri dintr-o categorie a unei variabile impartit la numarul de cazuri din toate categoriile variabilei respective.

Raport: numarul de cazuri dintr-o categorie a unei variabile impartit la numarul de cazuri din alta categorie a variabilei respective.

Rata: numarul de cazuri reale (efective) impartit la numarul de cazuri posibile pentru variabila de interes pe o anumita unitate de timp.