
|
|
|
Sa ne imaginam urmatoarea situatie (exemplul preluat dupa Cohen, 1996): cineva pretinde ca poate identifica oamenii cu inteligenta peste medie pe baza unei "puteri personale", la simpla apropiere de acestia, chiar fara sa-i vada. Sa presupunem ca ne hotaram sa verificam aceasta "putere psihica" ascunsa. In acest caz "posibilitatea de identificare a inteligentei pe baza unei abilitati paranormale" devine ipoteza de cercetare, cu alte cuvinte, ceea ce vrem sa demonstram[1][1]. In acest scop aducem in fata mediumului nostru un numar suficient de mare de subiecti (in alegerea carora "inteligenta" sa nu fie absolut de loc implicata) si ii cerem sa ii identifice pe cei pe care ii considera mai inteligenti decat media. Ulterior, ii supunem pe cei astfel alesi unui test de inteligenta si constatam ca valoarea QI medie a esantionului respectiv (sa presupunem, N=30) este m=104, cu o abatere standard s=19. Stiind ca media scorului QI la nivelul populatiei este 100, am putea fi tentati sa concluzionam ca, intr-adevar, persoana noastra are puterea de a indica subiectii cu inteligenta peste medie.
In acest moment ne amintim ca una dintre caracteristicile fundamentale ale metodei stiintifice este scepticismul. Ca urmare sunt cateva aspecte la care ne putem gandi in legatura cu datele obtinute in investigatia noastra:
o Esantionul indicat de medium ca fiind compus din oameni "mai inteligenti decat media" nu este decat unul din multele esantioane care ar putea fi selectate din populatie. Faptul ca esantionul selectat de medium are un QI mediu mai mare decat media populatiei se poate incadra in caracteristica oricarei medii de esantion de a oscila in jurul mediei populatiei de referinta.
o Ca urmare, ar fi posibil ca, fie si in absenta unei "puteri speciale", prin simpla indicare la intamplare, sa fie extras un esantion de subiecti al carui QI sa fie peste medie.
In consecinta, pentru a putea afirma ca mediumul dispune intr-adevar de puterea pe care o pretinde, trebuie sa dovedim ca nivelul de inteligenta al esantionului extras de el este mai mare decat al unui esantion extras absolut la intamplare.
Procedura statistica care se bazeaza pe acest rationament se numeste "ipoteza de nul" (se utilizeaza si alte variante de denumire: "ipoteza diferentei nule" sau pur si simplu "ipoteza statistica"). Ea implica o dovada indirecta a validitatii ipotezei cercetarii si se bazeaza pe un scenariu "negativ" (similar cu "a pune raul in fata"). Ipoteza de nul se formuleaza ca opusul ipotezei cercetarii. In cazul nostru ea va fi exprimata astfel: "nu exista o capacitate psihica speciala care sa permita identificare inteligentei superioare prin simpla proximitate spatiala".
Din punct de vedere formal, ipoteza de nul este simbolizata cu H0 iar ipoteza cercetarii cu H1. Dat fiind faptul ca ipoteza care este supusa efectiv testarii directe este ipoteza de nul, ipoteza cercetarii este denumita si "ipoteza alternativa".
Ne putem imagina o situatie in care rezultatul experimental (scorul mediu QI al esantionului indicat de mediu, in cazul nostru) este atat de bun incat sa nu existe nici o posibilitate de a se obtine un rezultat mai bun ca urmare a unei selectii pe baza de sansa? Teoretic, nu, curba normala fiind asimptotica, dar avem situatii in care aceasta sansa (probabilitatea) este atat de mica incat ne putem permite sa o consideram neglijabila. Intr-un asemenea caz, putem accepta ca valoarea obtinuta pe esantion nu decurge din variatia intamplatoare a mediei de esantionare ci provine din actiunea unui factor sistematic care a condus la indepartarea semnificativa a mediei esantionului de studiu de media populatiei.
Asa cum am mai spus anterior, extragerea unui numar mare de esantioane (eventual infinit de mare), produce ceea ce se numeste distributia de esantionare, care respecta legea curbei normale. Din perspectiva cercetarii statistice, aceasta distributie mai este denumita si distributia de nul deoarece ea arata cum se distribuie mediile esantioanelor posibile, daca acestea ar fi constituite pe o baza pur intamplatoare. Aceasta situatie reprezinta, de fapt, cazul in care ipoteza de nul ar fi adevarata.
Daca avem in vedere esantioane extrase la intamplare, despre acestea cunoastem sau putem afla:
o volumul, deoarece stim ca trebuie sa fie egal cu esantionul experimental;
o media distributiei de esantionare, deoarece presupunem cunoscuta media populatiei din care sunt extrase;
o eroarea standard, deoarece presupunem cunoscuta abaterea standard a populatiei (sau putem utiliza estimarea ei prin abaterea standard a esantionului) si avem volumul esantionului
Ca urmare, daca acceptam faptul ca distributia mediei de esantionare este normala, in conformitate cu teorema limitei centrale, putem utiliza tabela distributiei normale standard pentru a raspunde intrebarilor cu privire la media esantionului experimental, in acelasi mod in care am facut-o pentru notele z individuale.
Daca vrem sa stim care este probabilitatea de a obtine un rezultat mai bun prin jocul sansei, nu trebuie decat sa vedem unde se plaseaza rezultatul cercetarii pe distributia de nul. Apoi calculam aria de dincolo de acest punct, deoarece aceasta ne arata proportia (probabilitatea) cazurilor in care esantioane de aceeasi marime, selectate la intamplare, ar putea avea un QI mediu mai mare decat esantionul selectat de medium.
Sa revenim acum la exemplul nostru:
Am aflat ca, pentru esantionul extras de medium, avem urmatoarele valori statistice ale inteligentei: m=104, s=19, N=30. Ne amintim ca media inteligentei populatiei, exprimata in unitati QI este m=100 si abaterea standard s=16. Cu aceste date putem calcula nota z corespunzatoare esantionului nostru, cu formula:
![]()
(formula 3.4)
unde m este media esantionului, m este media populatiei, iar sm este eroarea standard a mediei.
Rezultatul calculului este:
![]()
In exemplul de mai sus, fiind vorba de QI, a carei abatere standard la nivelul populatiei ne este cunoscuta (am preferat valoarea 16) am utilizat-o ca atare. Daca ar fi fost vorba de o variabila pentru care nu cunosteam abaterea standard in populatie, am fi putut utiliza aceeasi valoare calculata pe esantionul de studiu.
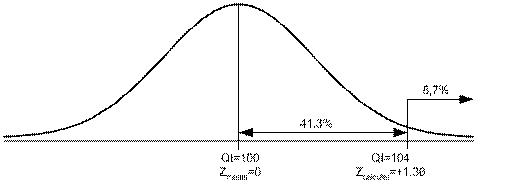
Daca plasam valoarea z calculata anterior, pe graficul distributiei normale, ca in figura de mai jos, observam ca intre media populatiei si nivelul inteligentei esantionului extras de medium" se afla 41.3% dintre valorile posibile si, implicit, ca exista 8.7% sanse (p=0.087) sa obtinem un esantion cu un QI mai mare decat cel indicat de medium, pe baza selectarii intamplatoare a subiectilor.
[1][1] Acesta este, desigur, un exemplu didactic. In realitate, inainte de a lansa o astfel de cercetare ar trebui sa ne documentam asupra fenomenului, sa studiem literatura de specialitate dar si rezultate ale altor cercetari. Abia la capatul acestui proces ar trebui sa decidem daca se justifica sau nu initierea unei cercetari pe o astfel de tema.